一、什么是delta方法

众所周知，当一个变量$X$服从正态分布时，其线性变换也服从正态分布。那么非线性变换呢？

delta方法提出，其经过可导函数变换后得到的$g(X)$仍然概率趋向正态分布，并且提供了期望、方差的计算公式。

单变量$X$ 变换为 $g(X)$，对$g(X)$泰勒展开：
$g(X)\approx g(\theta )+g^{\prime }(\theta )(X-\theta )$
$g(X)-g(\theta )\approx g^{\prime }(\theta )(X-\theta )\stackrel{\nu }{\to }N(0,{\sigma }^2\ast [g’(\theta ){]}^2)$

$g(\theta )$为常数，故$g(X)\to N(0,{\sigma }^2\ast [g^{\prime }(\theta ){]}^2)$

多变量变换同样能得到分布的期望和方差，常用于计算两随机变量之商$\frac{Y}{X}$的分布和方差

$E(\frac{Y}{X})=\frac{E(Y)}{E(X)}$
$var(\frac{Y}{X})=\frac{var(X)}{Y^2}+\frac{X^{2}var(Y)}{Y^4}-2\frac{Xcov(X,Y)}{Y^3}$

二、应用背景

AB测试中的随机化分流单元（Randomization Unit）和指标的分析单元（Analysis Unit） 不同时。中心极限定理要求样本点之间是独立的。AB实验中的分流单元是用户，即用户与用户之间独立。

• “人均”型指标的分析单元是用户，每个用户的取值为$X_1$，$X_2$，$X_3$…互相独立，此时$\bar{X}$可以用$z$检验。
• 点击率的分析单元是“每次曝光”，即是在曝光次数上求均值，样本点是$X_{11}$，$X_{12}$，$X_{13}$…，$X_{ij}$可看作第$i$个用户第$j$次曝光时是否点击，多次曝光互相之间不独立，无法用$z$检验。

解决方法：分子分母同时除以人数$n$，使用delta检验，得到$\overline{ctr}$服从正态分布，且可求得均值和方差。计算方差需要人均点击数/人均曝光量的均值和方差、以及人均点击和人均曝光的协方差。

进而计算统计量即可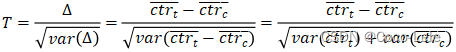

参考文献

https://www.jianshu.com/p/917dc1584452
https://toutiao.io/posts/q660w08/preview