向量究竟是什么？

物理专业的视角

从物理专业的视角来看，向量是空间中的箭头，决定该向量的特征为它的长度以及它的方向，只要这两个特征相同，你可以自由移动一个向量而保持它不变。

处在平面中的向量是二维的，而处在我们所生活的空间中的向量是三维的。

计算机专业视角

从计算机专业的视角来看，向量是有序的数字列表。

例如，假设对房价进行分析，可以用二维向量对房屋进行建模。第一个数字表示房屋面积，第二个数字表示价格。

在这里，“向量”只不过是“列表”的一个花哨的说法。

之所以这个向量是二维的，是因为这个列表长度为2。

数学专业视角

在数学专业视角，向量可以使任何东西，只需要它有意义即可。

二维向量的坐标

一个向量的坐标由一对数构成，这对数指导你如何从原点（向量起点）出发到达它的尖端（向量终点）。

第一个数告诉你沿着$x$轴走多远，第二个数告诉你沿着$y$轴走多远。

例如如下向量，就是沿着$x$轴走$-2.0$个单位长度，此后再沿着$y$轴走$-1.5$个单位长度。当长度为负数时，即为沿着与正方向相反的方向走。

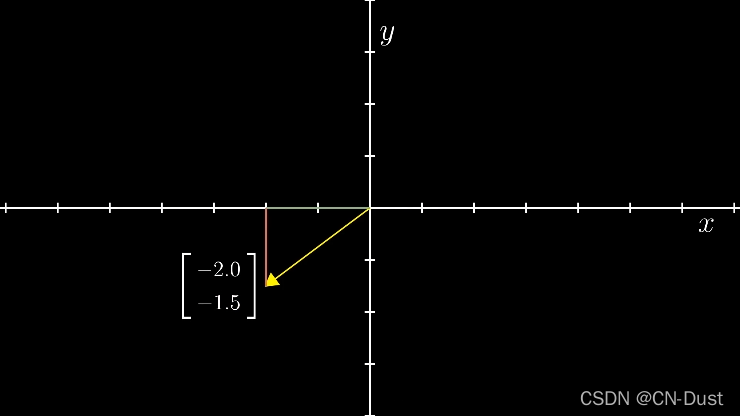
三维向量的坐标

在二维坐标系的基础上，添加垂直于$x$轴和$y$轴的第三根轴，叫它$z$轴。

在这种情况下，每个向量就有一个有序的三原数组与它对应。第一个数告诉你沿着$x$轴走多远，第二个数告诉你沿着$y$轴走多远，第三个数告诉你沿着$z$轴走多远。

向量加法和向量数乘

向量加法

假设图中两个向量相加，我们评议第二个向量，使它的起点和第一个向量的终点重合。

然后画一个向量，它从第一个向量的起点出发，指向第二个向量的终点。

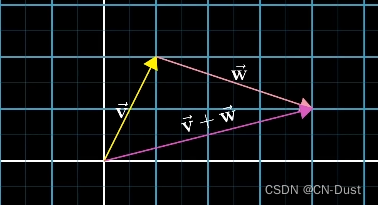
这个向量就是它们的和。
从数字的角度上看，第一个向量的坐标是$\left[\begin{array}{l}1\\ 2\end{array}\right]$，第二个向量的坐标是$\left[\begin{array}{l}3\\ -1\end{array}\right]$.

不难发现，和向量等于先向右移动$(1+3)$步，再向上移动$(2-1)$步。

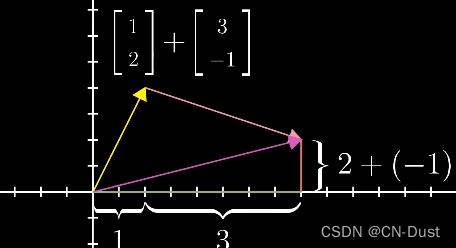
所以和向量为：
$$\left[\begin{array}{l}1\\ 2\end{array}\right]+\left[\begin{array}{l}3\\ -1\end{array}\right]=\left[\begin{array}{l}1+3\\ 2+(-1)\end{array}\right]$$

向量的加法就是把对应的数加起来。
$$\left[\begin{array}{l}{x}_1\\ y_1\end{array}\right]+\left[\begin{array}{l}{x}_2\\ y_2\end{array}\right]=\left[\begin{array}{l}{x}_1+x_2\\ y_1+y_2\end{array}\right]$$

向量数乘

向量数乘就是把向量拉长为原来的n倍。
例如：


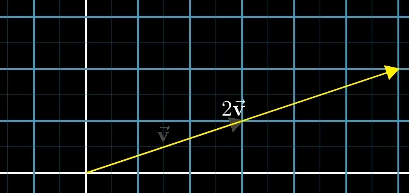
这里的$n$不具有向量的特性，就称为标量。

坐标系

一般情况下，$x$轴的正方向长度为1的向量与$y$轴的正方向长度为1的向量构成一个坐标系，不过，我们也可以自定义这两个单位向量，来改变我们的坐标系。

张成的空间

$\vec{v}$与$\vec{w}$全部线性组合构成的向量集合称为“张成的空间”。

当$\vec{v}$与$\vec{w}$不共线时，张成的空间为一个平面。

当$\vec{v}$与$\vec{w}$共线时，张成的空间为一条直线。

当$\vec{v}$与$\vec{w}$都为$\vec{0}$时，张成的空间为原点。

当然，这也适用于三维坐标系。

$\vec{v}$与$\vec{w}$与$\vec{u}$全部线性组合构成的向量集合称为“张成的空间”。