当前位置:网站首页>常微分方程的幂级数解法
常微分方程的幂级数解法
2022-08-09 14:52:00 【Chandler_river】
- 柯西定理
- 对于一阶微分方程
 .f(x,y)在区域内解析,也就是任取区域内一点(x0,y0)有
.f(x,y)在区域内解析,也就是任取区域内一点(x0,y0)有 。存在实数
。存在实数 使得初值问题在领域
使得初值问题在领域 内有唯一的解析解
内有唯一的解析解
- 对于一阶微分方程
- 幂级数解法
- 任何形如
 微分都可以转换成
微分都可以转换成 的形式.除非A(x0)=0的一些特殊点.这可能会导致方程在x0附近没有解析解,成为微分方程的奇点
的形式.除非A(x0)=0的一些特殊点.这可能会导致方程在x0附近没有解析解,成为微分方程的奇点 - 如果p(x)和q(x)在(x0-r,x0+r)可以展开为x-x0的幂级数,那么上述方程的解也可以在此区间表示为
 ,其中C0和C1为任意常数,后面的常数由它们确定.
,其中C0和C1为任意常数,后面的常数由它们确定.
- 任何形如
- 例题:


- 令a_{-1}=0,比较系数可得递推公式



- 勒让德方程

- 勒让德方程有两个奇点
 ,在
,在 有幂级数解
有幂级数解
- 代入,求得通项
- 解:
- 勒让德方程有两个奇点
- 勒让德多项式
- 勒让德方程的幂级数解可以表示为
 当
当 时,y1(x),y2(x)一定有一个是n次多项式.n为偶数时是y1(x) n为奇数时是y2(x) 总之,一定可以统一几位一个多项式Pn(x).
时,y1(x),y2(x)一定有一个是n次多项式.n为偶数时是y1(x) n为奇数时是y2(x) 总之,一定可以统一几位一个多项式Pn(x). - 勒让德多项式的性质
- 性质一:


- 性质二:
 .有级数展开式
.有级数展开式
- 递推公式:

- 性质四:函数系Pn(x)是正交的

- 性质一:
- 勒让德方程的幂级数解可以表示为
- 广义幂级数解法
- 针对A(x)y''+B(x)y'+C(x)y=0的奇点的解决方案

- 方程在
 内可表示为
内可表示为 - 指标和指标方程
- 针对A(x)y''+B(x)y'+C(x)y=0的奇点的解决方案
边栏推荐
猜你喜欢
![[DevOps] jekins configuration (2)](/img/d3/a6774cb8a1f99adf572653be0e581e.png)
[DevOps] jekins configuration (2)
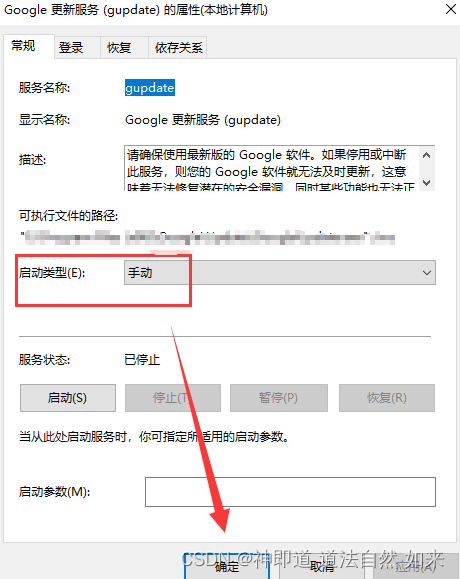
由于谷歌版本自动更新,导致selenium项目报错,如何关闭谷歌浏览器的自动更新?

和月薪5W的测试聊过后,才知道自己一直在打杂...

C语言程序设计笔记(浙大翁恺版) 第九周:指针

xshell7连接工具下载

DSPE-PEG-Aldehyde, DSPE-PEG-CHO, Phospholipid-PEG-Aldehyde MW: 1000

985测试工程师被吊打,学历和经验到底谁更重要?

Similar image detection method

Computer Graphics From Scratch - Chapter 5

易基因|作物育种:DNA甲基化在大豆优良品种培育中的作用研究成果
随机推荐
FilenameFilter filters filenames
C语言程序设计笔记(浙大翁恺版) 第十二周:程序结构
流程控制学习
Play in the cloud | The ever-changing gameplay of Tianyi cloud computer
OpenCV - 矩阵操作 Part 3
C语言程序设计笔记(浙大翁恺版) 第四周:循环
vivo手机上的系统级消息推送平台的架构设计实践
二维数组实现八皇后问题
Shell programming loop statement
注释,标识符,数据类型
shell之函数和数组
C语言程序设计笔记(浙大翁恺版) 第十一周:结构类型
08-Lock版的生产者消费者问题
一种基于视频帧差异视频卡顿检测方案
Mysql两个引擎对比
C语言程序设计笔记(浙大翁恺版) 第九周:指针
由于谷歌版本自动更新,导致selenium项目报错,如何关闭谷歌浏览器的自动更新?
C语言程序设计笔记(浙大翁恺版) 第二周:计算
卷积神经网络表征可视化研究综述(1)
正则表达式实战:最新豆瓣top250爬虫超详细教程
 .f(x,y)在区域内解析,也就是任取区域内一点(x0,y0)有
.f(x,y)在区域内解析,也就是任取区域内一点(x0,y0)有 。存在实数
。存在实数 使得初值问题在领域
使得初值问题在领域 内有唯一的解析解
内有唯一的解析解 微分都可以转换成
微分都可以转换成 的形式.除非A(x0)=0的一些特殊点.这可能会导致方程在x0附近没有解析解,成为微分方程的奇点
的形式.除非A(x0)=0的一些特殊点.这可能会导致方程在x0附近没有解析解,成为微分方程的奇点 ,其中C0和C1为任意常数,后面的常数由它们确定.
,其中C0和C1为任意常数,后面的常数由它们确定.





 ,在
,在 有幂级数解
有幂级数解
 当
当 时,y1(x),y2(x)一定有一个是n次多项式.n为偶数时是y1(x) n为奇数时是y2(x) 总之,一定可以统一几位一个多项式Pn(x).
时,y1(x),y2(x)一定有一个是n次多项式.n为偶数时是y1(x) n为奇数时是y2(x) 总之,一定可以统一几位一个多项式Pn(x). ![P_n(x)=-\frac{1}{2^n}\sum_{k=0}^{[\frac{n}{2}]}\frac{(-1)^k(2n-2k)!}{k!(n-k)!(n-2k)!}x^{n-2k}](http://img.inotgo.com/imagesLocal/202208/09/202208091450462712_2.gif)


 .有级数展开式
.有级数展开式



 内可表示为
内可表示为