代码随想录笔记_动态规划_70爬楼梯

代码随想录二刷笔记记录

LC70.爬楼梯

题目

完全背包

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶

示例2:

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示：

1 <= n <= 45

思路分析1

方法1：归纳

动态规划五部曲

1.确定dp数组和下标意义

dp[i] 的定义： 第 i 个数代表爬到第 i 层有 dp[i] 个方案

2.确定递推公式

要爬 n 阶楼梯，

设我们在第 n-1 层台阶时，有dp[n-1]个方案,再爬1个台阶就抵达楼顶.

在第 n-2 步时，有dp[n-2]个方案，再爬 2 个台阶就抵达楼顶。

设求爬 n 阶楼梯的函数为 f ,则有

f(n) = f(n-1) + f(n-2)

dp[i] = dp[i-1] + dp[i-2]

3.dp数组初始化

依题意，最少要2个台阶，因此第0层没有方法 -> dp[0] = 0 (这里无论dp[0] = 多少，都是没有意义的，因为遍历从dp[2]开始，所以 dp[0] 无论等于1 还是 0 都无所谓)

第1层有 1 种方法，就是一个台阶 dp[1] = 1,

第2层有 2 种方法，1+1 和 2 ,因此 dp[2] = 2

4.确定遍历顺序

由递推公式 dp[i] = dp[i-1] + dp[i-2] 可知， 第 i 层阶梯的方案要依赖于第 i-1 层有dp[i-1]个方案和第 i-2 层有 dp[i-2] 个方案，因此是从前往后遍历。

5.推演分析

以 n = 6 为例

dp[3] = 3, dp[4] = 5 ,dp[5] = 8,dp[6] = 13

代码实现1

完整代码实现

public int climbStairs(int n) {
    
		//特判
        if (n <= 2) return n;
        //初始化
        int[] dp = new int[2];
        dp[1] = 1;
        dp[2] = 2;
        int method = 0;
        //遍历
        for (int i = 3;i <= n;i++){
    
            method = dp[i-1] + dp[i-2];
            dp[i-2] = dp[i-1];
            dp[i-1] = method;
        }
        return method;
    }

思路分析2

方法2：动态规划_完全背包

以完全背包的方法解答 70 题

由题，分析可知： 物品为 一阶台阶，二阶台阶。背包容量：爬到楼顶的层数

台阶可以重复取，因此本题是一个完全背包问题。

动态规划五部曲

1.确定dp数组及其下标含义

dp[j]: 爬到 j 层的楼,有 dp[j] 种方法

2.递推公式

由 LC494，377，518 可知，回顾求装满背包共有几种方法的递推公式

dp[j] += dp[j - nums[i]]

而本题，求第 j 层台阶的方法dp[j] , 由之前的dp[j-1],dp[j-2],… 推导而来

因此，递推公式为

dp[j] += dp[j-i]

3.初始化

dp[0] = 1,和之前的题目LC494，377，518一样，第一项需要初始化为1，否则会影响后续的推导。

4.遍历顺序

由示例2可知，1阶 + 2阶 和 2阶 + 1阶 不同，因此可以确定，本题所求的答案是各种排列的总数。求排列，我们采用的遍历顺序为先遍历背包，后遍历物品。

for(i = 0;i <= n;i++){
     //背包
	for(j = 1;j <= 2;j++){
    //物品
		if(i >= j){
     //当背包容量 >= 物品时,计算才有意义
			dp[i] += dp[i - j];
		}
	}
}

5.推演分析

以 n = 3 为例

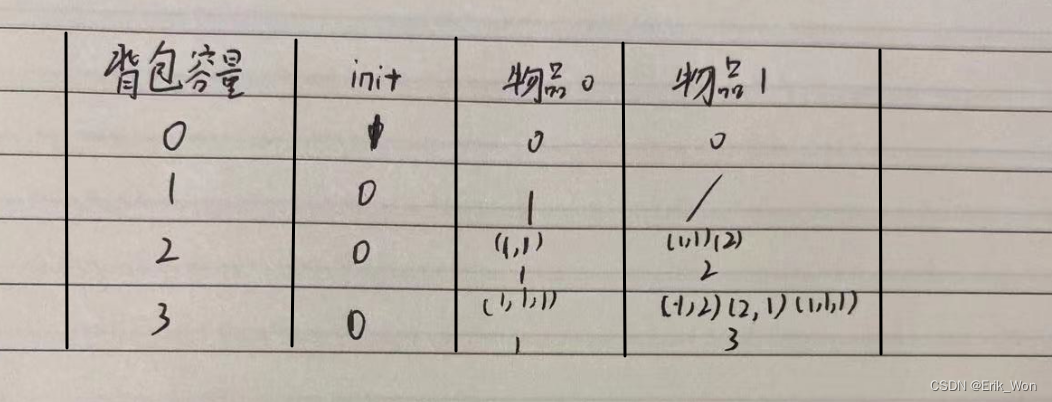
代码实现2

public int climbStairs(int n) {
    
        if (n <= 2) return n;
    	//初始化
        int[] dp = new int[n + 1];
        dp[0] = 1;
    //先遍历背包，后遍历物品
        for (int i = 0; i <= n; i++) {
     //背包
            for (int j = 1; j <= 2; j++) {
     //物品
                //背包容量 > 物品时，才开始更新
                if (i >= j){
    
                    dp[i] += dp[i - j];
                }
            }
        }
        return dp[n];
    }

总结

针对本题的完全背包用法，进行一个回顾
1.递推公式
针对组合问题，我们一般采用的公式都是

dp[i] += dp[j - nums[i]]

2.遍历顺序
组合问题我们还需要考虑遍历顺序的问题，根据题目给出的示例，我们可以判断，如：(1,2) 和 (2,1) 是否是同一个答案。是，则代表题目考虑的是组合问题；否，则代表我们所求的是排列问题。

• 组合问题：先遍历物品，后遍历背包
• 排列问题：先遍历背包，后遍历物品

小拓展

一步一个台阶，两个台阶，三个台阶，直到 m个台阶，有多少种方法走到 n 阶楼顶。

代码实现

public int climbStairs(int n) {
    
        int[] dp = new int[n+1];
        dp[0] = 1;
        for (int i = 1;i <= n;i++){
    
        	for(int j = 1; j<= m; j++){
    
        	//m表示最多可以爬m个台阶
        		if(i - j >= 0) dp[i] += dp[i-j];
        	}
        }
        return dp[n];
 }