当前位置:网站首页>Anxun cup 2021_ Crypto_ Reappearance
Anxun cup 2021_ Crypto_ Reappearance
2022-04-21 21:25:00 【M3ng@L】
An Xun Cup 2021_Crypto_ Reappear
- little_trick
-
- d p , d q discharge dew dp,dq Let the cat out of the dp,dq discharge dew
- P r o b l e m Problem Problem
- A n a l y s i s Analysis Analysis
- S o l v i n g c o d e Solving~code Solving code
- C o n c l u s i o n Conclusion Conclusion
- U n e x p e c t e d s o l u t i o n Unexpected~solution Unexpected solution
- strage
- ez_eqution
- air encryption
little_trick
k e y w o r d s : keywords: keywords: python_random modular ,RSA dp&dq Let the cat out of the ,(~a|b) & (a|~b) Logical expression operation
d p , d q discharge dew dp,dq Let the cat out of the dp,dq discharge dew
Classic about dp,dq Let the cat out of the , Is known RSA Encrypted dp,dq,p,q,c
among dp,dq Respectively satisfy
d p ≡ d ( m o d ( p − 1 ) ) d q ≡ d ( m o d ( q − 1 ) ) dp \equiv d\pmod {(p-1)}\\ dq \equiv d\pmod {(q-1)} dp≡d(mod(p−1))dq≡d(mod(q−1))
How to deduce plaintext from the above known conditions m Well ?
Try to make the above two congruences Equivalent
Formula derivation
set up
{ m p ≡ c d p ( m o d p ) m q ≡ c d q ( m o d q ) ⇒ { m p ≡ c d ( m o d ( p − 1 ) ) ( m o d p ) m q ≡ c d ( m o d ( q − 1 ) ) ( m o d q ) \begin{cases} m_p\equiv c^{dp}\pmod p\\ m_q \equiv c^{dq}\pmod q \end{cases} \Rightarrow \begin{cases} m_p \equiv c^{d\pmod{(p-1)}}\pmod p\\ m_q \equiv c^{d\pmod {(q-1)}}\pmod q \end{cases} {
mp≡cdp(modp)mq≡cdq(modq)⇒{
mp≡cd(mod(p−1))(modp)mq≡cd(mod(q−1))(modq)
from Euler theorem a ϕ ( m ) ≡ 1 ( m o d m ) a^{\phi(m)}\equiv 1\pmod m aϕ(m)≡1(modm), among a a a And m m m Relatively prime ; therefore ϕ ( p ) = p − 1 \phi(p)=p-1 ϕ(p)=p−1, therefore c p − 1 ≡ 1 ( m o d p ) c^{p-1}\equiv 1\pmod p cp−1≡1(modp)
{ m p ≡ c d ( m o d ( p − 1 ) ) ( m o d p ) m q ≡ c d ( m o d ( q − 1 ) ) ( m o d q ) * { m p ≡ c d + k 1 ′ ⋅ ( p − 1 ) ( m o d p ) m q ≡ c d + k 2 ′ ⋅ ( q − 1 ) ( m o d q ) * { m p ≡ c d ( m o d p ) m q ≡ c d ( m o d q ) \begin{cases} m_p \equiv c^{d\pmod{(p-1)}}\pmod p\\ m_q \equiv c^{d\pmod {(q-1)}}\pmod q \end{cases} \iff \begin{cases} m_p \equiv c^{d+k_1'\cdot (p-1)}\pmod p \\ m_q \equiv c^{d+k_2'\cdot (q-1)}\pmod q \end{cases} \iff \begin{cases} m_p \equiv c^{d}\pmod p \\ m_q \equiv c^{d}\pmod q \end{cases} {
mp≡cd(mod(p−1))(modp)mq≡cd(mod(q−1))(modq)*{
mp≡cd+k1′⋅(p−1)(modp)mq≡cd+k2′⋅(q−1)(modq)*{
mp≡cd(modp)mq≡cd(modq)
Then, after derivation, we get ** m p , m q m_p,m_q mp,mq Equivalent to plain text m In the parting mold p,q Value in the case of **
So we can c^d Is the intermediate quantity , Establish an equation between two congruences
Convert congruence into ordinary equation
m p + k 1 ⋅ p = m q + k 2 ⋅ q ⇒ k 1 ⋅ p = m q − m p + k 2 ⋅ q m_p+k_1\cdot p=m_q+k_2\cdot q\\ \Rightarrow k_1\cdot p = m_q-m_p + k_2\cdot q mp+k1⋅p=mq+k2⋅q⇒k1⋅p=mq−mp+k2⋅q
Now there are two unknowns on both sides of the equation k 1 , k 2 k_1,k_2 k1,k2, But one of the unknowns can be transformed into a remainder operation , So you can calculate the value on one side of the equation
k 1 ⋅ p ≡ m q − m p ( m o d q ) ⇒ k 1 ≡ p − 1 ⋅ ( m q − m p ) ( m o d q ) k_1\cdot p \equiv m_q-m_p \pmod q\\ \Rightarrow k_1\equiv p^{-1} \cdot(m_q-m_p)\pmod q k1⋅p≡mq−mp(modq)⇒k1≡p−1⋅(mq−mp)(modq)
among p − 1 p^{-1} p−1 yes p p p Yes, modulus q q q Inverse element , That is to say p ⋅ p − 1 ≡ 1 ( m o d q ) p\cdot p^{-1}\equiv 1\pmod q p⋅p−1≡1(modq)
So we can calculate k 1 k_1 k1 Size , Then we can go back to the previous equation ( After derivation, we get m p ≡ c d p ≡ c d ( m o d p ) m_p\equiv c^{dp}\equiv c^{d}\pmod p mp≡cdp≡cd(modp))
m p ≡ c d ( m o d p ) ⇒ c d = m p + k 1 ⋅ p m_p\equiv c^{d}\pmod p\\ \Rightarrow c^{d}=m_p+k_1\cdot p mp≡cd(modp)⇒cd=mp+k1⋅p
It can be calculated that c^d, Calculate again c d ( m o d ( p ⋅ q ) ) c^d \pmod {(p\cdot q)} cd(mod(p⋅q)), Get real plaintext m
Implementation script
from Crypto.Util.number import long_to_bytes
import gmpy2
p = ...
q = ...
dp = ...
dq = ...
c = ...
inv_p = gmpy2.invert(p,q)
mp = pow(c,dp,p)
mq = pow(c,dq,q)
m = (((mq - mp) * inv_p) % q) + mp
m = m % (p * q)
print(long_to_bytes(m).decode())
P r o b l e m Problem Problem
from Crypto.Util.number import sieve_base, bytes_to_long, getPrime
import random
import gmpy2
import os
flag = b'D0g3{}'
flag = bytes_to_long(flag)
p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = gmpy2.next_prime(bytes_to_long(os.urandom(3)))
c = gmpy2.powmod(flag,e,n)
print(p)
print(q)
print(c)
dp = ''
seeds = []
for i in range(0,len(dp)):
seeds.append(random.randint(0,99))
print(seeds)
result = []
for j in range(0,len(dp)):
random.seed(seeds[j])
rands = []
for k in range(0,4):
rands.append(random.randint(0,99))
result.append((~ord(dp[j])|rands[j%4]) & (ord(dp[j])|~rands[j%4]))
del rands[j%4]
print(rands)
print(result)
dq = ''
C = []
E = 0x10001
list_p = sieve_base[0:len(dq)]
list_q = sieve_base[len(dq):2*len(dq)]
for l in range(0,len(dq)):
P = list_p[l]
Q = list_q[l]
C.append(pow(int(dq[l]),E,P*Q))
print(C)
A n a l y s i s Analysis Analysis
In the face of flag The encryption uses the standard RSA, But it didn't give e, Instead, it gives p,q; According to the script after dp,dq Toss of , It can be judged that it is to recover first dp,dq, Then apply RSA dp&dq The leaked script can
Recovering dp In the process of , The key is
result.append((~ord(dp[j])|rands[j%4]) & (ord(dp[j])|~rands[j%4]))
You can put ta It is simply regarded as a logical operation equation
( ¬ a ∨ b ) ∧ ( a ∨ ¬ b ) (\lnot a \vee b)\land (a\vee \lnot b) (¬a∨b)∧(a∨¬b)
among ∨ \vee ∨ The operation priority of is higher than ∧ \land ∧, So in my opinion, it's not easy to simplify , Since there are only two values , Then we will Truth table Get it out and have a look ta What is the special nature of
| a a a | b b b | ( ¬ a ∨ b ) ∧ ( a ∨ ¬ b ) (\lnot a \vee b)\land (a\vee \lnot b) (¬a∨b)∧(a∨¬b) |
|---|---|---|
| 0 0 0 | 0 0 0 | 1 1 1 |
| 0 0 0 | 1 1 1 | 0 0 0 |
| 1 1 1 | 0 0 0 | 0 0 0 |
| 1 1 1 | 1 1 1 | 1 1 1 |
It can be found through observation , as long as a , b a,b a,b Different results are 0 0 0, For the same 1 1 1
Interestingly, if we take the result of the logical expression as a a a perhaps b b b Do another logical expression operation , The result is the same as the original a a a perhaps b b b identical
in other words
set up f ( a , b ) = ( ¬ a ∨ b ) ∧ ( a ∨ ¬ b ) , be f ( f ( a , b ) , b ) = a f ( a , f ( a , b ) ) = b set up f(a,b)=(\lnot a \vee b)\land (a\vee \lnot b), be \\ f(f(a,b),b) = a\\ f(a,f(a,b)) = b set up f(a,b)=(¬a∨b)∧(a∨¬b), be f(f(a,b),b)=af(a,f(a,b))=b
PS: Later, I found that this is Exclusive or The nature of , Look up the XOR logical expression
a ⊕ b = ( ¬ a ∧ b ) ∨ ( ¬ b ∧ a ) a \oplus b=(\lnot a\land b)\vee(\lnot b \land a) a⊕b=(¬a∧b)∨(¬b∧a)
The logical expression used in this problem is actually ¬ ( a ⊕ b ) \lnot(a\oplus b) ¬(a⊕b)
So according to
for j in range(0,len(dp)):
random.seed(seeds[j])
rands = []
for k in range(0,4):
rands.append(random.randint(0,99))
result.append((~ord(dp[j])|rands[j%4]) & (ord(dp[j])|~rands[j%4]))
del rands[j%4]
print(rands)
We only need to generate the same... As in the script encryption process rands Sequence , In fact, it is in the operation of logical expression b
Then take the result of the first round of logical expression operation as a new a, Continue a round of logical expression operation to get the original a, That is to say dp
About generating rands Sequence , Confirmation used in the title seed, Make the random number generated each time the same (random The module adopts pseudo-random number generator ), for instance
>>> import random
>>> random.seed(50)
>>> random.randint(0,99)
63
>>> random.seed(50)
>>> random.randint(0,99)
63
The title gives seeds Seed sequence , We just need to repeat the same script settings
First, the default is python3 Resume dp, But I found that in the end dp It's a strange string , Then we compare the results of the non key sequence given by the title rands The random number in ,python3 call random.seed() The generated rands Is different from the title ( That's why the topic should put the non key part rands Print out ); since python3 Generated differences , Just have a try python2 Of random modular
Get the right results
result1 = [-38, -121, -40, -125, -51, -29, -2, -21, -59, -54, -51, -40, -105, -5, -4, -50, -127, -56, -124, -128, -23, -104, -63, -112, -34, -115, -58, -99, -24, -102, -1, -5, -34, -3, -104, -103, -21, -62, -121, -24, -115, -9, -87, -56, -39, -30, -34, -4, -33, -5, -114, -21, -19, -7, -119, -107, -115, -6, -25, -27, -32, -62, -28, -20, -60, -121, -102, -10, -112, -7, -85, -110, -62, -100, -110, -29, -41, -55, -113, -112, -45, -106, -125, -25, -57, -27, -83, -2, -51, -118, -2, -10, -50, -40, -1, -82, -111, -113, -50, -48, -23, -33, -112, -38, -29, -26, -4, -40, -123, -4, -44, -120, -63, -38, -41, -22, -50, -50, -17, -122, -61, -5, -100, -22, -44, -47, -125, -125, -127, -55, -117, -100, -2, -26, -32, -111, -123, -118, -16, -24, -20, -40, -92, -40, -102, -49, -99, -45, -59, -98, -49, -13, -62, -128, -121, -114, -112, -13, -3, -4, -26, -35, -15, -35, -8, -18, -125, -14, -6, -60, -113, -104, -120, -64, -104, -55, -104, -41, -34, -106, -105, -2, -28, -14, -58, -128, -3, -1, -17, -38, -18, -12, -59, -4, -19, -82, -40, -122, -18, -42, -53, -60, -113, -40, -126, -15, -63, -40, -124, -114, -58, -26, -35, -26, -8, -48, -112, -52, -11, -117, -52, -32, -21, -38, -124, -13, -103, -6, -30, -33, -28, -31, -1, -97, -59, -64, -28, -1, -40, -2, -10, -26, -24, -3, -50, -113, -125, -122, -124, -5, -50, -62, -11, -8, -88, -109, -7, -31, -105, -54, -28, -8, -62, -58, -101, -58, -53, -124, -18, -124, -17, -109, -52, -45, -40, -109, -85, -7, -108, -121, -58, -49, -91, -102, -8, -10, -17, -55, -19, -11, -116, -47, -120, -121, -23, -99, -19, -51, -36, -110, -126, -29, -110, -9, -97, -54, -83, -86]
seeds = [3, 0, 39, 78, 14, 49, 73, 83, 55, 48, 30, 28, 23, 16, 54, 23, 68, 7, 20, 8, 98, 68, 45, 36, 97, 13, 83, 68, 16, 59, 81, 26, 51, 45, 36, 60, 36, 94, 58, 11, 19, 33, 95, 12, 60, 38, 51, 95, 21, 3, 38, 72, 47, 80, 7, 20, 26, 80, 18, 43, 92, 4, 64, 93, 91, 12, 86, 63, 46, 73, 89, 5, 91, 17, 88, 94, 80, 42, 90, 14, 45, 53, 91, 16, 28, 81, 62, 63, 66, 20, 81, 3, 43, 99, 54, 22, 2, 27, 2, 62, 88, 99, 78, 25, 76, 49, 28, 96, 95, 57, 94, 53, 32, 58, 32, 72, 89, 15, 4, 78, 89, 74, 86, 45, 51, 65, 13, 75, 95, 42, 20, 77, 34, 66, 56, 20, 26, 18, 28, 11, 88, 62, 72, 27, 74, 42, 63, 76, 82, 97, 75, 92, 1, 5, 20, 78, 46, 85, 81, 54, 64, 87, 37, 91, 38, 39, 1, 90, 61, 28, 13, 60, 37, 90, 87, 15, 78, 91, 99, 58, 62, 73, 70, 56, 82, 5, 19, 54, 76, 88, 4, 3, 55, 3, 3, 22, 85, 67, 98, 28, 32, 42, 48, 96, 69, 3, 83, 48, 26, 20, 45, 16, 45, 47, 92, 0, 54, 4, 73, 8, 31, 38, 3, 10, 84, 60, 59, 69, 64, 91, 98, 73, 81, 98, 9, 70, 44, 44, 24, 95, 83, 49, 31, 19, 89, 18, 20, 78, 86, 95, 83, 23, 42, 51, 95, 80, 48, 46, 88, 7, 47, 64, 55, 4, 62, 37, 71, 75, 98, 67, 98, 58, 66, 70, 24, 58, 56, 44, 11, 78, 1, 78, 89, 97, 83, 72, 98, 12, 41, 33, 14, 40, 27, 5, 18, 35, 25, 31, 69, 97, 84, 47, 25, 90, 78, 15, 72, 71]
ls_dp = []
for j in range(len(seeds)):
random.seed(seeds[j])
rands = []
for k in range(0,4):
rands.append(random.randint(0,99))
ls_dp.append((~result1[j]|rands[j%4]) & (result1[j]|~rands[j%4]))
print(rands,end="")
print("".join([chr(i) for i in ls_dp]))
# 23458591381644494879596426183878928641891759871602961070839457303969747353773411708437315165237216481430908369709167907047043280248152040749469402814146054871536032870746473649690743697560576735624528397398691515920649222501258921802372365480019200479555430922883680472732415240714991623845227274793947921407
Then recover dq
dq = ''
C = []
E = 0x10001
list_p = sieve_base[0:len(dq)]
list_q = sieve_base[len(dq):2*len(dq)]
for l in range(0,len(dq)):
P = list_p[l]
Q = list_q[l]
C.append(pow(int(dq[l]),E,P*Q))
print(C)
dq The encryption process is much simpler , among sieve_base By 2 2 2 To 104729 104729 104729 A sequence of prime numbers of
So we actually know P and Q And the given C and E, So solution pow(dp[l],E,P*Q) Isn't it easy
# recovery dq
E = 0x10001
C = [1, 0, 7789, 1, 17598, 20447, 15475, 23040, 41318, 23644, 53369, 19347, 66418, 5457, 0, 1, 14865, 97631, 6459, 36284, 79023, 1, 157348, 44667, 185701, 116445, 23809, 220877, 0, 1, 222082, 30333, 55446, 207442, 193806, 149389, 173229, 349031, 152205, 1, 149157, 196626, 1, 222532, 10255, 46268, 171536, 0, 351788, 152678, 0, 172225, 109296, 0, 579280, 634746, 1, 668942, 157973, 1, 17884, 662728, 759841, 450490, 0, 139520, 157015, 616114, 199878, 154091, 1, 937462, 675736, 53200, 495985, 307528, 1, 804492, 790322, 463560, 520991, 436782, 762888, 267227, 306436, 1051437, 384380, 505106, 729384, 1261978, 668266, 1258657, 913103, 935600, 1, 1, 401793, 769612, 484861, 1024896, 517254, 638872, 1139995, 700201, 308216, 333502, 0, 0, 401082, 1514640, 667345, 1015119, 636720, 1011683, 795560, 783924, 1269039, 5333, 0, 368271, 1700344, 1, 383167, 7540, 1490472, 1484752, 918665, 312560, 688665, 967404, 922857, 624126, 889856, 1, 848912, 1426397, 1291770, 1669069, 0, 1709762, 130116, 1711413, 1336912, 2080992, 820169, 903313, 515984, 2211283, 684372, 2773063, 391284, 1934269, 107761, 885543, 0, 2551314, 2229565, 1392777, 616280, 1368347, 154512, 1, 1668051, 0, 2453671, 2240909, 2661062, 2880183, 1376799, 0, 2252003, 1, 17666, 1, 2563626, 251045, 1593956, 2215158, 0, 93160, 0, 2463412, 654734, 1, 3341062, 3704395, 3841103, 609968, 2297131, 1942751, 3671207, 1, 1209611, 3163864, 3054774, 1055188, 1, 4284662, 3647599, 247779, 0, 176021, 3478840, 783050, 4613736, 2422927, 280158, 2473573, 2218037, 936624, 2118304, 353989, 3466709, 4737392, 2637048, 4570953, 1473551, 0, 0, 4780148, 3299784, 592717, 538363, 2068893, 814922, 2183138, 2011758, 2296545, 5075424, 1814196, 974225, 669506, 2756080, 5729359, 4599677, 5737886, 3947814, 4852062, 1571349, 4123825, 2319244, 4260764, 1266852, 1, 3739921, 1, 5948390, 1, 2761119, 2203699, 1664472, 3182598, 6269365, 5344900, 454610, 495499, 6407607, 1, 1, 476694, 4339987, 5642199, 1131185, 4092110, 2802555, 0, 5323448, 1103156, 2954018, 1, 1860057, 128891, 2586833, 6636077, 3136169, 1, 3280730, 6970001, 1874791, 48335, 6229468, 6384918, 5412112, 1, 7231540, 7886316, 2501899, 8047283, 2971582, 354078, 401999, 6427168, 4839680, 1, 44050, 3319427, 0, 1, 1452967, 4620879, 5525420, 5295860, 643415, 5594621, 951449, 1996797, 2561796, 6707895, 7072739]
list_p = sieve_base[0:len(C)]
list_q = sieve_base[len(C):2*len(C)]
for i in range(len(C)):
P = list_p[i]
Q = list_q[i]
phi_N = (P - 1) * (Q - 1)
D = gmpy2.invert(E,phi_N)
print(pow(C[i],D,P*Q),end="")
# 104137587579880166582178434901328539485184135240660490271571544307637817287517428663992284342411864826922600858353966205614398977234519495034539643954586905495941906386407181383904043194285771983919780892934288899562700746832428876894943676937141813284454381136254907871626581989544814547778881240129496262777
Last dp,dq Successful recovery , Directly cover the previous RSA dp&dq Just leak the script
S o l v i n g c o d e Solving~code Solving code
import random
from Crypto.Util.number import *
import gmpy2
p = 119494148343917708105807117614773529196380452025859574123211538859983094108015678321724495609785332508563534950957367289723559468197440246960403054020452985281797756117166991826626612422135797192886041925043855329391156291955066822268279533978514896151007690729926904044407542983781817530576308669792533266431
q = 125132685086281666800573404868585424815247082213724647473226016452471461555742194042617318063670311290694310562746442372293133509175379170933514423842462487594186286854028887049828613566072663640036114898823281310177406827049478153958964127866484011400391821374773362883518683538899757137598483532099590137741
c = 10238271315477488225331712641083290024488811710093033734535910573493409567056934528110845049143193836706122210303055466145819256893293429223389828252657426030118534127684265261192503406287408932832340938343447997791634435068366383965928991637536875223511277583685579314781547648602666391656306703321971680803977982711407979248979910513665732355859523500729534069909408292024381225192240385351325999798206366949106362537376452662264512012770586451783712626665065161704126536742755054830427864982782030834837388544811172279496657776884209756069056812750476669508640817369423238496930357725842768918791347095504283368032
# # recovery dp
# result1 = [-38, -121, -40, -125, -51, -29, -2, -21, -59, -54, -51, -40, -105, -5, -4, -50, -127, -56, -124, -128, -23, -104, -63, -112, -34, -115, -58, -99, -24, -102, -1, -5, -34, -3, -104, -103, -21, -62, -121, -24, -115, -9, -87, -56, -39, -30, -34, -4, -33, -5, -114, -21, -19, -7, -119, -107, -115, -6, -25, -27, -32, -62, -28, -20, -60, -121, -102, -10, -112, -7, -85, -110, -62, -100, -110, -29, -41, -55, -113, -112, -45, -106, -125, -25, -57, -27, -83, -2, -51, -118, -2, -10, -50, -40, -1, -82, -111, -113, -50, -48, -23, -33, -112, -38, -29, -26, -4, -40, -123, -4, -44, -120, -63, -38, -41, -22, -50, -50, -17, -122, -61, -5, -100, -22, -44, -47, -125, -125, -127, -55, -117, -100, -2, -26, -32, -111, -123, -118, -16, -24, -20, -40, -92, -40, -102, -49, -99, -45, -59, -98, -49, -13, -62, -128, -121, -114, -112, -13, -3, -4, -26, -35, -15, -35, -8, -18, -125, -14, -6, -60, -113, -104, -120, -64, -104, -55, -104, -41, -34, -106, -105, -2, -28, -14, -58, -128, -3, -1, -17, -38, -18, -12, -59, -4, -19, -82, -40, -122, -18, -42, -53, -60, -113, -40, -126, -15, -63, -40, -124, -114, -58, -26, -35, -26, -8, -48, -112, -52, -11, -117, -52, -32, -21, -38, -124, -13, -103, -6, -30, -33, -28, -31, -1, -97, -59, -64, -28, -1, -40, -2, -10, -26, -24, -3, -50, -113, -125, -122, -124, -5, -50, -62, -11, -8, -88, -109, -7, -31, -105, -54, -28, -8, -62, -58, -101, -58, -53, -124, -18, -124, -17, -109, -52, -45, -40, -109, -85, -7, -108, -121, -58, -49, -91, -102, -8, -10, -17, -55, -19, -11, -116, -47, -120, -121, -23, -99, -19, -51, -36, -110, -126, -29, -110, -9, -97, -54, -83, -86]
# seeds = [3, 0, 39, 78, 14, 49, 73, 83, 55, 48, 30, 28, 23, 16, 54, 23, 68, 7, 20, 8, 98, 68, 45, 36, 97, 13, 83, 68, 16, 59, 81, 26, 51, 45, 36, 60, 36, 94, 58, 11, 19, 33, 95, 12, 60, 38, 51, 95, 21, 3, 38, 72, 47, 80, 7, 20, 26, 80, 18, 43, 92, 4, 64, 93, 91, 12, 86, 63, 46, 73, 89, 5, 91, 17, 88, 94, 80, 42, 90, 14, 45, 53, 91, 16, 28, 81, 62, 63, 66, 20, 81, 3, 43, 99, 54, 22, 2, 27, 2, 62, 88, 99, 78, 25, 76, 49, 28, 96, 95, 57, 94, 53, 32, 58, 32, 72, 89, 15, 4, 78, 89, 74, 86, 45, 51, 65, 13, 75, 95, 42, 20, 77, 34, 66, 56, 20, 26, 18, 28, 11, 88, 62, 72, 27, 74, 42, 63, 76, 82, 97, 75, 92, 1, 5, 20, 78, 46, 85, 81, 54, 64, 87, 37, 91, 38, 39, 1, 90, 61, 28, 13, 60, 37, 90, 87, 15, 78, 91, 99, 58, 62, 73, 70, 56, 82, 5, 19, 54, 76, 88, 4, 3, 55, 3, 3, 22, 85, 67, 98, 28, 32, 42, 48, 96, 69, 3, 83, 48, 26, 20, 45, 16, 45, 47, 92, 0, 54, 4, 73, 8, 31, 38, 3, 10, 84, 60, 59, 69, 64, 91, 98, 73, 81, 98, 9, 70, 44, 44, 24, 95, 83, 49, 31, 19, 89, 18, 20, 78, 86, 95, 83, 23, 42, 51, 95, 80, 48, 46, 88, 7, 47, 64, 55, 4, 62, 37, 71, 75, 98, 67, 98, 58, 66, 70, 24, 58, 56, 44, 11, 78, 1, 78, 89, 97, 83, 72, 98, 12, 41, 33, 14, 40, 27, 5, 18, 35, 25, 31, 69, 97, 84, 47, 25, 90, 78, 15, 72, 71]
# tmp = "[54, 36, 60] [84, 42, 25] [20, 38, 39] [81, 9, 92] [70, 65, 94] [6, 11, 75] [27, 50, 46] [49, 85, 8] [95, 14, 73] [54, 71, 30] [53, 28, 65] [11, 13, 59] [94, 89, 8] [36, 41, 44] [91, 13, 48] [92, 94, 89] [94, 74, 90] [32, 65, 7] [90, 68, 90] [22, 96, 12] [83, 35, 5] [74, 74, 90] [27, 48, 33] [32, 98, 95] [80, 37, 84] [25, 68, 84] [49, 85, 37] [74, 94, 74] [48, 41, 44] [22, 94, 2] [50, 45, 38] [74, 20, 20] [50, 16, 82] [27, 8, 33] [32, 98, 91] [30, 57, 26] [98, 95, 91] [54, 28, 43] [58, 20, 94] [45, 55, 92] [78, 52, 51] [57, 81, 27] [76, 51, 53] [47, 65, 66] [57, 26, 80] [63, 72, 6] [24, 50, 82] [76, 51, 99] [68, 63, 47] [23, 36, 60] [63, 42, 6] [7, 59, 98] [43, 45, 34] [27, 70, 95] [32, 15, 7] [90, 68, 76] [20, 20, 60] [27, 70, 95] [18, 66, 19] [3, 69, 14] [56, 55, 58] [23, 39, 15] [47, 63, 92] [91, 49, 56] [17, 68, 16] [47, 66, 14] [79, 3, 31] [44, 29, 90] [39, 58, 85] [27, 56, 46] [8, 60, 14] [62, 74, 79] [17, 68, 16] [52, 96, 28] [39, 18, 62] [54, 12, 28] [54, 70, 95] [63, 27, 22] [20, 9, 58] [10, 70, 65] [48, 8, 33] [61, 45, 71] [8, 17, 16] [36, 48, 41] [13, 59, 17] [50, 55, 38] [92, 17, 23] [44, 29, 90] [43, 24, 44] [90, 76, 90] [50, 45, 38] [23, 54, 36] [69, 14, 46] [40, 17, 24] [91, 13, 48] [95, 14, 2] [94, 5, 8] [64, 95, 19] [95, 94, 8] [92, 17, 97] [18, 90, 62] [40, 17, 24] [81, 9, 73] [37, 92, 84] [95, 20, 29] [6, 11, 75] [11, 13, 17] [37, 90, 39] [51, 99, 53] [4, 1, 51] [54, 12, 43] [61, 89, 45] [21, 30, 90] [58, 64, 94] [7, 21, 90] [7, 59, 98] [60, 99, 14] [96, 73, 15] [23, 10, 15] [81, 9, 92] [60, 99, 14] [85, 11, 12] [79, 3, 31] [27, 48, 8] [50, 16, 82] [41, 84, 44] [25, 68, 84] [45, 43, 4] [51, 99, 53] [63, 27, 22] [90, 68, 90] [79, 32, 24] [58, 84, 89] [7, 24, 44] [96, 55, 52] [90, 68, 76] [20, 20, 60] [18, 33, 19] [11, 13, 17] [45, 55, 92] [18, 90, 62] [92, 97, 23] [7, 59, 34] [64, 70, 95] [51, 11, 12] [63, 27, 22] [44, 29, 48] [37, 95, 20] [48, 50, 96] [19, 37, 84] [45, 43, 76] [42, 56, 55] [84, 76, 25] [62, 79, 94] [90, 68, 90] [81, 9, 92] [39, 58, 85] [19, 10, 90] [50, 45, 38] [91, 13, 55] [63, 40, 92] [14, 83, 54] [68, 9, 84] [8, 17, 68] [42, 72, 6] [20, 19, 39] [13, 84, 25] [20, 9, 65] [55, 80, 32] [11, 59, 17] [25, 68, 84] [30, 57, 26] [9, 61, 84] [20, 65, 58] [14, 18, 54] [96, 1, 73] [9, 92, 73] [8, 68, 16] [40, 20, 24] [58, 20, 64] [17, 97, 23] [27, 56, 46] [90, 29, 13] [96, 55, 47] [48, 50, 96] [62, 79, 94] [67, 78, 51] [91, 13, 55] [95, 20, 29] [39, 90, 62] [23, 10, 15] [23, 54, 36] [95, 14, 73] [23, 36, 60] [23, 54, 60] [95, 14, 2] [61, 10, 90] [7, 97, 41] [35, 83, 5] [11, 13, 59] [21, 30, 90] [63, 27, 22] [54, 13, 30] [37, 90, 39] [9, 16, 60] [23, 36, 60] [49, 85, 37] [54, 13, 71] [20, 20, 60] [90, 76, 90] [27, 48, 33] [36, 48, 41] [48, 8, 33] [35, 45, 34] [42, 56, 58] [84, 75, 42] [13, 55, 48] [23, 39, 15] [27, 50, 46] [22, 96, 12] [11, 39, 68] [63, 72, 6] [23, 54, 60] [57, 42, 57] [91, 3, 0] [30, 26, 80] [22, 93, 2] [68, 9, 16] [63, 40, 92] [8, 68, 16] [35, 83, 5] [27, 50, 56] [45, 55, 38] [35, 35, 5] [46, 37, 86] [90, 29, 45] [54, 86, 17] [40, 86, 17] [71, 83, 99] [76, 51, 99] [85, 8, 37] [6, 11, 75] [1, 11, 68] [67, 78, 52] [60, 99, 14] [18, 33, 19] [90, 68, 90] [81, 9, 92] [3, 83, 31] [76, 99, 53] [49, 85, 37] [92, 94, 89] [2, 27, 22] [24, 16, 82] [76, 51, 53] [27, 54, 70] [13, 71, 30] [88, 58, 85] [39, 18, 62] [32, 15, 65] [43, 45, 34] [47, 40, 92] [9, 95, 73] [23, 10, 39] [17, 97, 23] [68, 61, 84] [32, 62, 98] [45, 43, 4] [83, 35, 5] [7, 97, 41] [35, 83, 5] [58, 20, 64] [43, 24, 44] [90, 45, 13] [71, 83, 99] [58, 20, 64] [55, 47, 52] [40, 86, 17] [45, 55, 46] [81, 9, 92] [84, 76, 25] [81, 92, 73] [8, 60, 14] [19, 80, 37] [85, 8, 37] [7, 98, 34] [35, 83, 5] [47, 65, 66] [23, 16, 91] [57, 81, 27] [10, 70, 94] [45, 87, 3] [70, 95, 19] [62, 79, 94] [18, 66, 19] [54, 75, 74] [92, 84, 21] [1, 39, 68] [68, 9, 60] [19, 80, 37] [91, 3, 0] [35, 45, 34] [37, 92, 21] [20, 9, 65] [9, 92, 73] [96, 73, 15] [7, 59, 34] [32, 62, 0]"
# ls_dp = []
# for j in range(len(seeds)):
# random.seed(seeds[j])
# rands = []
# for k in range(0,4):
# rands.append(random.randint(0,99))
# ls_dp.append((~result1[j]|rands[j%4]) & (result1[j]|~rands[j%4]))
# print(rands,end="")
# print("".join([chr(i) for i in ls_dp]))
# 23458591381644494879596426183878928641891759871602961070839457303969747353773411708437315165237216481430908369709167907047043280248152040749469402814146054871536032870746473649690743697560576735624528397398691515920649222501258921802372365480019200479555430922883680472732415240714991623845227274793947921407
dp = 23458591381644494879596426183878928641891759871602961070839457303969747353773411708437315165237216481430908369709167907047043280248152040749469402814146054871536032870746473649690743697560576735624528397398691515920649222501258921802372365480019200479555430922883680472732415240714991623845227274793947921407
# recovery dq
E = 0x10001
C = [1, 0, 7789, 1, 17598, 20447, 15475, 23040, 41318, 23644, 53369, 19347, 66418, 5457, 0, 1, 14865, 97631, 6459, 36284, 79023, 1, 157348, 44667, 185701, 116445, 23809, 220877, 0, 1, 222082, 30333, 55446, 207442, 193806, 149389, 173229, 349031, 152205, 1, 149157, 196626, 1, 222532, 10255, 46268, 171536, 0, 351788, 152678, 0, 172225, 109296, 0, 579280, 634746, 1, 668942, 157973, 1, 17884, 662728, 759841, 450490, 0, 139520, 157015, 616114, 199878, 154091, 1, 937462, 675736, 53200, 495985, 307528, 1, 804492, 790322, 463560, 520991, 436782, 762888, 267227, 306436, 1051437, 384380, 505106, 729384, 1261978, 668266, 1258657, 913103, 935600, 1, 1, 401793, 769612, 484861, 1024896, 517254, 638872, 1139995, 700201, 308216, 333502, 0, 0, 401082, 1514640, 667345, 1015119, 636720, 1011683, 795560, 783924, 1269039, 5333, 0, 368271, 1700344, 1, 383167, 7540, 1490472, 1484752, 918665, 312560, 688665, 967404, 922857, 624126, 889856, 1, 848912, 1426397, 1291770, 1669069, 0, 1709762, 130116, 1711413, 1336912, 2080992, 820169, 903313, 515984, 2211283, 684372, 2773063, 391284, 1934269, 107761, 885543, 0, 2551314, 2229565, 1392777, 616280, 1368347, 154512, 1, 1668051, 0, 2453671, 2240909, 2661062, 2880183, 1376799, 0, 2252003, 1, 17666, 1, 2563626, 251045, 1593956, 2215158, 0, 93160, 0, 2463412, 654734, 1, 3341062, 3704395, 3841103, 609968, 2297131, 1942751, 3671207, 1, 1209611, 3163864, 3054774, 1055188, 1, 4284662, 3647599, 247779, 0, 176021, 3478840, 783050, 4613736, 2422927, 280158, 2473573, 2218037, 936624, 2118304, 353989, 3466709, 4737392, 2637048, 4570953, 1473551, 0, 0, 4780148, 3299784, 592717, 538363, 2068893, 814922, 2183138, 2011758, 2296545, 5075424, 1814196, 974225, 669506, 2756080, 5729359, 4599677, 5737886, 3947814, 4852062, 1571349, 4123825, 2319244, 4260764, 1266852, 1, 3739921, 1, 5948390, 1, 2761119, 2203699, 1664472, 3182598, 6269365, 5344900, 454610, 495499, 6407607, 1, 1, 476694, 4339987, 5642199, 1131185, 4092110, 2802555, 0, 5323448, 1103156, 2954018, 1, 1860057, 128891, 2586833, 6636077, 3136169, 1, 3280730, 6970001, 1874791, 48335, 6229468, 6384918, 5412112, 1, 7231540, 7886316, 2501899, 8047283, 2971582, 354078, 401999, 6427168, 4839680, 1, 44050, 3319427, 0, 1, 1452967, 4620879, 5525420, 5295860, 643415, 5594621, 951449, 1996797, 2561796, 6707895, 7072739]
list_p = sieve_base[0:len(C)]
list_q = sieve_base[len(C):2*len(C)]
for i in range(len(C)):
P = list_p[i]
Q = list_q[i]
phi_N = (P - 1) * (Q - 1)
D = gmpy2.invert(E,phi_N)
print(pow(C[i],D,P*Q),end="")
# 104137587579880166582178434901328539485184135240660490271571544307637817287517428663992284342411864826922600858353966205614398977234519495034539643954586905495941906386407181383904043194285771983919780892934288899562700746832428876894943676937141813284454381136254907871626581989544814547778881240129496262777
dq = 104137587579880166582178434901328539485184135240660490271571544307637817287517428663992284342411864826922600858353966205614398977234519495034539643954586905495941906386407181383904043194285771983919780892934288899562700746832428876894943676937141813284454381136254907871626581989544814547778881240129496262777
print()
inv_p = gmpy2.invert(p,q)
mp = pow(c,dp,p)
mq = pow(c,dq,q)
m = (((mq - mp) * inv_p) % q) + mp
m = m % (p * q)
print(long_to_bytes(m).decode())
C o n c l u s i o n Conclusion Conclusion
About logical expressions , It's usually Simplification Or write Truth table Find the nature of the approach
python2 Of random Module and python3 Of random The pseudo-random number generator algorithm used in the module is different
U n e x p e c t e d s o l u t i o n Unexpected~solution Unexpected solution
Some solutions are that since the problem has been given e e e Value range of , Then let's blast directly e e e, The judgment condition is the final plaintext m Include in D0g3
because RSA Medium p,q,c All known , So we blow up e It's easy to solve
strage
k e y w o r d s : keywords: keywords: Compared with the plaintext size hint Small , Truth table ,coppersmith
P r o b l e m Problem Problem
from Crypto.Util.number import *
import os
flag = b'D0g3{}'
m = bytes_to_long(flag)
p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = 3
hint = bytes_to_long(os.urandom(256))
m1 = m | hint
m2 = m & hint
c = pow(m1, e, n)
with open('output.txt','a') as f:
f.write(str([n,c,m2,hint]))
f.close()
A n a l y s i s Analysis Analysis
Title known n,c,m2,hint
and m2 = m & hint, Unknown m1 yes m1 = n | hint
If you look at this question carefully, you will find that the p,q The use of RSA Not directly to flag Encrypted , But the encryption is m1
and m1 = m | hint, in other words m1.bit_length() = hint.bit_length(), Why is equal to hint Binary bit length instead of m The binary bit length of ? because
hint = bytes_to_long(os.urandom(256))
in other words hint The binary bit length of is 2048, And the known m2 = m & hint, therefore m2 The binary bit length of is equal to m
m2.bit_length()
# 383
So in m1 in , The binary bit length is greater than 383 All the parts are hint In itself , instead of hint or m Result ;
in addition m1 The binary bit length of is too large , Although here RSA Encryption uses e Only 3, But the third power has also made pow(m1,3) > n
So it can't be used Low encryption index attack
But for later calculations, only the whole m1 Before 383 Binary bits , So we can put what we really need before 383 A number consisting of binary bits as an unknown number , and m1 The remaining bits we actually know ( Namely hint Corresponding binary bit of ), To construct a new equation
c ≡ ( h i g h _ m 1 + l o w _ m 1 ) 3 ( m o d n ) c\equiv (high\_m_1 + low\_m_1)^{3}\pmod n c≡(high_m1+low_m1)3(modn)
Because the binary digits of unknowns satisfy coppersmith The required conditions of the theorem , So use coppersmith Theorem can be solved
high_m1 = (hint >> 383) * pow(2,383)
PR.<x> = PolynomialRing(Zmod(n))
f = (high_m1 + x) ^ 3 - c
f.small_roots(2^383,beta = 0.4)
Get m1 Before 383 Bit binary
Now let's look at the whole , We know m1,m2,hint
and m1 = m | hint,m2 = m & hint; It's actually a simple logical operation , Two numbers of two equations are known , Find the remaining number , Make a brief list of Truth table ( Take the value of a single binary bit as an example )
If
hint == 0, Then at this time, due to And operation The nature of ,m2It must be0, And now whenm1 == 0when ,mIt must be0, Whenm1 == 1when ,mIt must be1( It can also be said that ,m == m1)If
hint == 1, Then at this time, due to Or operations The nature of ,m1It must be1, And now whenm2 == 0when ,mIt must be0, Whenm2 == 1when ,mIt must be1( It can also be said that ,m == m2)
We can restore through the above properties m Each binary bit of
Originally, it was to put m1,m2,hint First convert to binary form , Then judge one by one , But the binary bits may be misplaced , Lead to flag Only a few are right
Use similar to LSFR Stream cipher generation process to restore m Binary bit of
m = ""
while m2 > 0: # m1 Can also be
a = hint & 1
b = m1 & 1
c = m2 & 1
if a == 0:
assert c == 0
m += str(b)
if a == 1:
assert b == 1
m += str(c)
hint = hint >> 1
m1 = m1 >> 1
m2 = m2 >> 1
m = m[::-1] # Because of the original m It's in reverse order , So turn it over
s o l v i n g c o d e solving~code solving code
from Crypto.Util.number import *
import gmpy2
n,c,m2,hint = (13002904520196087913175026378157676218772224961198751789793139372975952998874109513709715017379230449514880674554473551508221946249854541352973100832075633211148140972925579736088058214014993082226530875284219933922497736077346225464349174819075866774069797318066487496627589111652333814065053663974480486379799102403118744672956634588445292675676671957278976483815342400168310432107890845293789670795394151784569722676109573685451673961309951157399183944789163591809561790491021872748674809148737825709985578568373545210653290368264452963080533949168735319775945818152681754882108865201849467932032981615400210529003, 8560367979088389639093355670052955344968008917787780010833158290316540154791612927595480968370338549837249823871244436946889198677945456273317343886485741297260557172704718731809632734567349815338988169177983222118718585249696953103962537942023413748690596354436063345873831550109098151014332237310265412976776977183110431262893144552042116871747127301026195142320678244525719655551498368460837394436842924713450715998795899172774573341189660227254331656916960984157772527015479797004423165812493802730996272276613362505737536007284308929288293814697988968407777480072409184261544708820877153825470988634588666018802, 9869907877594701353175281930839281485694004896356038595955883788511764488228640164047958227861871572990960024485992, 9989639419782222444529129951526723618831672627603783728728767345257941311870269471651907118545783408295856954214259681421943807855554571179619485975143945972545328763519931371552573980829950864711586524281634114102102055299443001677757487698347910133933036008103313525651192020921231290560979831996376634906893793239834172305304964022881699764957699708192080739949462316844091240219351646138447816969994625883377800662643645172691649337353080140418336425506119542396319376821324619330083174008060351210307698279022584862990749963452589922185709026197210591472680780996507882639014068600165049839680108974873361895144)
high_m1 = (hint >> int(m2).bit_length()) * pow(2,int(m2).bit_length())
PR.<x> = PolynomialRing(Zmod(n))
f = (high_m1 + x) ^ 3 - c
low_m1 = f.small_roots(2^int(m2).bit_length(),beta=0.4)[0]
low_m1 = 13420866878657192881981508918368509601760484822510871697454710042290632315733970543259862148639047993224391010676733
m1 = low_m1
assert int(m2).bit_length() == int(m1).bit_length()
m = ""
while m2 > 0:
a = hint & 1
b = m1 & 1
c = m2 & 1
if a == 0:
assert c == 0
m += str(b)
if a == 1:
assert b == 1
m += str(c)
hint = hint >> 1
m1 = m1 >> 1
m2 = m2 >> 1
m = "0" + m[::-1]
print(long_to_bytes(int(m,2)).decode())
ez_eqution
k e y w o r d s : keywords: keywords: Extract the greatest common factor , Solving quadratic equation of one variable ,RSA p,q Close to the situation
P r o b l e m Problem Problem
from Crypto.Util.number import *
from functools import reduce
import os
pad1 = os.urandom(256)
pad2 = os.urandom(256)
flag = b'D0g3{}'
primelist = [getPrime(1024) for i in range(3)]
p = getPrime(1024)
q = nextprime(p)
n = reduce(lambda a, b:a * b, primelist) * p * q
x1 = pow(primelist[0],2)
x2 = pow(primelist[1],2)
x3 = primelist[0] * primelist[1]
y1 = x1 * primelist[1] + x2 * primelist[0]
y2 = x2 * (primelist[2] + 1) - 1
y3 = x3 * (primelist[2] + 1) - 1
m = bytes_to_long(pad1+flag+pad2)
e = 0x10001
c = pow(m,e,n)
print('#M1=',y1 + x2 + x3)
print('#M2=',y2 + y3)
print('#c=',c)
print('#n=',n)
#M1=
#M2=
#c=
#n=
A n a l y s i s Analysis Analysis
Yes pad1 + flag + pad2 Conduct RSA encryption , Obviously, the plaintext is big enough , There can be no unexpected solution such as direct square root ; Let's take a look again n Construction
primelist = [getPrime(1024) for i in range(3)]
p = getPrime(1024)
q = nextprime(p)
n = reduce(lambda a, b:a * b, primelist) * p * q
The effect is equivalent to n = primelist[0] * primelist[1] * primelist[2] * p * q
In order to solve flag, We need to know fai_n, At least I know primelist[i] Size ( And then it's going to be primelist[i] writing pi)
The title gives M1,M2; among
M 1 = p 1 2 ⋅ p 0 + p 1 ⋅ p 0 2 + p 0 ⋅ p 1 + p 1 2 M 2 = ( p 1 2 + p 0 ⋅ p 1 ) ⋅ ( p 2 + 1 ) − 2 M_1=p_1^2\cdot p_0+p_1\cdot p_0^2 + p_0\cdot p_1+p_1^2\\ M_2=(p_1^2+p_0\cdot p_1)\cdot(p_2+1)-2 M1=p12⋅p0+p1⋅p02+p0⋅p1+p12M2=(p12+p0⋅p1)⋅(p2+1)−2
It was obvious M 1 , M 2 + 2 M_1,M_2+2 M1,M2+2 There must be a common divisor p 1 p_1 p1
M 1 = p 1 ⋅ ( p 1 ⋅ p 0 + p 0 2 + p 0 + p 1 ) M 2 + 2 = p 1 ⋅ ( p 1 + p 0 ) ⋅ ( p 2 + 1 ) M_1=p_1\cdot(p_1\cdot p_0 + p_0^2 + p_0+p_1)\\ M_2+2= p_1\cdot(p_1+p_0)\cdot(p_2 + 1) M1=p1⋅(p1⋅p0+p02+p0+p1)M2+2=p1⋅(p1+p0)⋅(p2+1)
But according to the calculated results , The greatest common divisor of the two is not equal to p 1 p_1 p1
>>> import gmpy2
>>> p1 = gmpy2.gcd(M1,M2 + 2)
>>> p1.bit_length()
2051
# Correct p1 Of bit_length() It should be equal to 1024
The reason is probably M 1 , M 2 + 2 M_1,M_2+2 M1,M2+2 The result of the addition in brackets involved in is likely to contain more and larger common factors , The maximum common divisor of the whole is not equal to p 1 p_1 p1, It's equal to p 1 ⋅ u n k n o w n p_1\cdot unknown p1⋅unknown;( in other words M 1 M_1 M1 Medium ( p 1 ⋅ p 0 + p 0 2 + p 0 + p 1 ) (p_1\cdot p_0 + p_0^2 + p_0+p_1) (p1⋅p0+p02+p0+p1) and M 2 + 2 M_2+2 M2+2 Medium ( p 1 + p 0 ) ⋅ ( p 2 + 1 ) (p_1+p_0)\cdot(p_2 + 1) (p1+p0)⋅(p2+1) There are probably other common divisors , Lead to M 1 , M 2 + 2 M_1,M_2+2 M1,M2+2 The greatest common divisor of is not just p 1 p_1 p1)
Also tried blasting u n k n o w n unknown unknown Size , But it contains a larger number , Cause failure of blasting
But it contains p 1 p_1 p1 The known quantity as a factor is not only M 2 + 2 M_2+2 M2+2, modulus n n n It also contains p 1 p_1 p1 As a factor , And no redundant addition leads to the generation of common factors of non prime numbers , Try it
>>> import gmpy2
>>> p1 = gmpy2.gcd(M1,n)
>>> p1.bit_length()
1024 # correct
So I want to put p 1 p_1 p1 Output as the greatest common divisor of two numbers , It is required that all parts of the composition of at least one number have no new factor
p1 We know , Now replace M1 Solve to p 0 p_0 p0 A univariate quadratic equation as an unknown number
M 1 = p 0 2 ⋅ p 1 + p 0 ⋅ ( p 1 2 + p 1 ) + p 1 2 M_1= p_0^2\cdot p_1 + p_0\cdot(p_1^2+ p_1)+p_1^2 M1=p02⋅p1+p0⋅(p12+p1)+p12
You can push with your hand Matching method , You can also directly substitute sagemath solve
p0 = var("p0")
f = p0 ^ 2 + p0 * (p1 + 1) + p1 - (M1//p1)
solve(p0 ^ 2 + p0 * (p1 + 1) + p1 == M1 // p1,p0)[1]
# 117379993488408909213785887974472229016071265566403849836216754847295401565166151872329440545598767396499252325133419296775798211888305050776586647999185549171166433935032159605367762650398185050063643611720499373962310459705000471248897299568458251778545586376091559089442503748421906239117101764062329447353
Matching method
M 1 p 1 − p 1 + 1 4 ⋅ ( p 1 + 1 ) 2 = p 0 2 + p 0 ⋅ ( p 1 + 1 ) + 1 4 ⋅ ( p 1 + 1 ) 2 = ( p 0 + 1 2 ( p 1 + 1 ) ) 2 \frac{M_1}{p_1}-p_1+\frac{1}{4}\cdot(p_1+1)^2 = p_0^2+p_0\cdot(p_1+1)+\frac{1}{4}\cdot(p_1+1)^2=(p_0+\frac{1}{2}(p_1+1))^2 p1M1−p1+41⋅(p1+1)2=p02+p0⋅(p1+1)+41⋅(p1+1)2=(p0+21(p1+1))2
f = (M1 // p1) - p1 + ((p1 + 1) ** 2) // 4
p0 = gmpy2.iroot(f,2)[0] - (p1 + 1) // 2
Now we know p0,p1, Daihui M2 Solve directly p2 that will do
p2 = (M2 + 2) // (p1**2 + p0 * p1) - 1
Finally known p0,p1,p2 Now it's left p,q Unknown ; and p,q Is an adjacent prime number , We can calculate p*q Size , Then you can open the square , Find the two adjacent prime numbers of the square number
pq = n // p0 // p1 // p2
q = nextprime(gmpy2.iroot(pq,2)[0])
p = prevprime(q)
Last p,q,p0,p1,p2 All known , Then it can be solved normally RSA 了
S o l v i n g c o d e Solving~code Solving code
from Crypto.Util.number import *
import gmpy2
from sympy import *
M1= 3826382835023788442651551584905620963555468828948525089808250303867245240492543151274589993810948153358311949129889992078565218014437985797623260774173862776314394305207460929010448541919151371739763413408901958357439883687812941802749556269540959238015960789123081724913563415951118911225765239358145144847672813272304000303248185912184454183649550881987218183213383170287341491817813853157303415010621029153827654424674781799037821018845093480149146846916972070471616774326658992874624717335369963316741346596692937873980736392272357429717437248731018333011776098084532729315221881922688633390593220647682367272566275381196597702434911557385351389179790132595840157110385379375472525985874178185477024824406364732573663044243615168471526446290952781887679180315888377262181547383953231277148364854782145192348432075591465309521454441382119502677245090726728912738123512316475762664749771002090738886940569852252159994522316
M2= 4046011043117694641224946060698160981194371746049558443191995592417947642909277226440465640195903524402898673255622570650810338780358645872293473212692240675287998097280715739093285167811740252792986119669348108850168574423371861266994630851360381835920384979279568937740516573412510564312439718402689547377548575653450519989914218115265842158616123026997554651983837361028152010675551489190669776458201696937427188572741833635865019931327548900804323792893273443467251902886636756173665823644958563664967475910962085867559357008073496875191391847757991101189003154422578662820049387899402383235828011830444034463049749668906583814229827321704450021715601349950406035896249429068630164092309047645766216852109121662629835574752784717997655595307873219503797996696389945782836994848995124776375146245061787647756704605043856735398002012276311781956668212776588970619658063515356931386886871554860891089498456646036630114620806
c= 1394946766416873131554934453357121730676319808212515786127918041980606746238793432614766163520054818740952818682474896886923871330780883504028665380422608364542618561981233050210507202948882989763960702612116316321009210541932155301216511791505114282546592978453573529725958321827768703566503841883490535620591951871638499011781864202874525798224508022092610499899166738864346749753379399602574550324310119667774229645827773608873832795828636770263111832990012205276425559363977526114225540962861740929659841165039419904164961095126757294762709194552018890937638480126740196955840656602020193044969685334441405413154601311657668298101837066325231888411018908300828382192203062405287670490877283269761047853117971492197659115995537837080400730294215778540754482680476723953659085854297184575548489544772248049479632420289954409052781880871933713121875562554234841599323223793407272634167421053493995795570508435905280269774274084603687516219837730100396191746101622725880529896250904142333391598426588238082485305372659584052445556638990497626342509620305749829144158797491411816819447836265318302080212452925144191536031249404138978886262136129250971366841779218675482632242265233134997115987510292911606736878578493796260507458773824689843424248233282828057027197528977864826149756573867022173521177021297886987799897923182290515542397534652789013340264587028424629766689059507844211910072808286250914059983957934670979551428204569782238857331272372035625901349763799005621577332502957693517473861726359829588419409120076625939502382579605
n= 19445950132976386911852381666731799463510958712950274248183192405937223343228119407660772413067599252710235310402278345391806863116119010697766434743302798644091220730819441599784039955347398797545219314925103529062092963912855489464914723588833817280786158985269401131919618320866942737291915603551320163001129725430205164159721810319128999027215168063922977994735609079166656264150778896809813972275824980250733628895449444386265971986881443278517689428198251426557591256226431727934365277683559038777220498839443423272238231659356498088824520980466482528835994554892785108805290209163646408594682458644235664198690503128767557430026565606308422630014285982847395405342842694189025641950775231191537369161140012412147734635114986068452144499789367187760595537610501700993916441274609074477086105160306134590864545056872161818418667370690945602050639825453927168529154141097668382830717867158189131567590506561475774252148991615602388725559184925467487450078068863876285937273896246520621965096127440332607637290032226601266371916124456122172418136550577512664185685633131801385265781677598863031205194151992390159339130895897510277714768645984660240750580001372772665297920679701044966607241859495087319998825474727920273063120701389749480852403561022063673222963354420556267045325208933815212625081478538158049144348626000996650436898760300563194390820694376019146835381357141426987786643471325943646758131021529659151319632425988111406974492951170237774415667909612730440407365124264956213064305556185423432341935847320496716090528514947
e = 65537
p1 = int(gmpy2.gcd(M1,n))
# print(p1.bit_length())
f = (M1 // p1) - p1 + ((p1 + 1) ** 2) // 4
p0 = gmpy2.iroot(f,2)[0] - (p1 + 1) // 2
p2 = (M2 + 2) // (p1**2 + p0 * p1) - 1
pq = n // p0 // p1 // p2
q = nextprime(gmpy2.iroot(pq,2)[0])
p = prevprime(q)
fai_n = (p-1) * (q-1) * (p0 - 1) * (p1 - 1) * (p2 - 1)
d = gmpy2.invert(e,fai_n)
m = pow(c,d,n)
print(long_to_bytes(m)[256:-256].decode())
C o n c l u s i o n Conclusion Conclusion
Find the greatest common divisor of two variables , You need to make sure that there are no redundant invisible common factors in the expression ( It is usually generated by addition and subtraction ) appear
RSA p,q Close The situation should be directly p*q Find the adjacent prime number by the square of the result
air encryption
k e y w o r d s : keywords: keywords: AES_CTR,xor, Interaction , Euler theorem , Data processing
P r o b l e m Problem Problem
#!/usr/bin/python
import socketserver
import random
import os
import string
import binascii
import hashlib
from Crypto.Cipher import AES
from Crypto.Util import Counter
from Crypto.Util.number import getPrime
from hashlib import sha256
import gmpy2
from flag import flag
def init():
q = getPrime(512)
p = getPrime(512)
e = getPrime(64)
n = q*p
phi = (q-1) * (p-1)
d = gmpy2.invert(e, phi)
hint = 2 * d + random.randint(0, 2**16) * e * phi
mac = random.randint(0, 2**64)
c = pow(mac, e, n)
counter = random.randint(0, 2**128)
key = os.urandom(16)
score = 0
return n, hint, c, counter, key, mac, score
class task(socketserver.BaseRequestHandler):
def POW(self):
random.seed(os.urandom(8))
proof = ''.join([random.choice(string.ascii_letters+string.digits) for _ in range(20)])
result = hashlib.sha256(proof.encode('utf-8')).hexdigest()
self.request.sendall(("sha256(XXXX+%s) == %s\n" % (proof[4:],result)).encode())
self.request.sendall(b'Give me XXXX:\n')
x = self.recv()
if len(x) != 4 or hashlib.sha256((x+proof[4:].encode())).hexdigest() != result:
return False
return True
def recv(self):
BUFF_SIZE = 2048
data = b''
while True:
part = self.request.recv(BUFF_SIZE)
data += part
if len(part) < BUFF_SIZE:
break
return data.strip()
def padding(self, msg):
return msg + chr((16 - len(msg)%16)).encode() * (16 - len(msg)%16)
def encrypt(self, msg):
msg = self.padding(msg)
if self.r != -1:
self.r += 1
aes = AES.new(self.key, AES.MODE_CTR, counter = Counter.new(128, initial_value=self.r))
return aes.encrypt(msg)
else:
return msg
def send(self, msg, enc=True):
print(msg, end= ' ')
if enc:
msg = self.encrypt(msg)
print(msg, self.r)
self.request.sendall(binascii.hexlify(msg) + b'\n')
def set_key(self, rec):
if self.mac == int(rec[8:]):
self.r = self.counter
def guess_num(self, rec):
num = random.randint(0, 2**128)
if num == int(rec[10:]):
self.send(b'right')
self.score += 1
else:
self.send(b'wrong')
def get_flag(self, rec):
assert self.r != -1
if self.score == 5:
self.send(flag, enc=False)
else:
self.send(os.urandom(32) + flag)
def handle(self):
self.r = -1
if not self.POW():
self.send(b'Error Hash!', enc= False)
return
self.n, self.hint, self.c ,self.counter, self.key, self.mac, self.score = init()
self.send(str(self.n).encode(), enc = False)
self.send(str(self.hint).encode(), enc = False)
self.send(str(self.c).encode(), enc = False)
for _ in range(6):
rec = self.recv()
if rec[:8] == b'set key:':
self.set_key(rec)
elif rec[:10] == b'guess num:':
self.guess_num(rec)
elif rec[:8] == b'get flag':
self.get_flag(rec)
else:
self.send(b'something wrong, check your input')
class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
pass
def main():
HOST, PORT = '127.0.0.1', 10086
server = ForkedServer((HOST, PORT), task)
server.allow_reuse_address = True
server.serve_forever()
if __name__ == '__main__':
main()
A n a l y s i s Analysis Analysis
Classic password nc Connecting questions , Careful observation shows that the key function is handle()
def handle(self):
self.r = -1
if not self.POW():
self.send(b'Error Hash!', enc= False)
return
self.n, self.hint, self.c ,self.counter, self.key, self.mac, self.score = init()
self.send(str(self.n).encode(), enc = False)
self.send(str(self.hint).encode(), enc = False)
self.send(str(self.c).encode(), enc = False)
for _ in range(6):
rec = self.recv()
if rec[:8] == b'set key:':
self.set_key(rec)
elif rec[:10] == b'guess num:':
self.guess_num(rec)
elif rec[:8] == b'get flag':
self.get_flag(rec)
else:
self.send(b'something wrong, check your input')
to POW Function validation ( It is equivalent to slowing down the running speed of the script ), It is judgement. hash value , Just blow it up
according to RSA The way of encryption gives n,c and hint( Note that the values given by the server are converted to hexadecimal through bytes , Need to return to normal bytes , The original byte is a decimal number , So use binascii.unhexlify()), And the encrypted plaintext is mac; The first ta Find out
h i n t = 2 ⋅ d + r a n d o m ⋅ e ⋅ ϕ ( n ) ∵ a ϕ ( p ) ≡ 1 ( m o d p ) , o PULL set The reason is ∴ c h i n t ≡ c 2 ⋅ d ⋅ c r a n d o m ⋅ e ⋅ ϕ ( n ) ≡ c 2 ⋅ d ( m o d n ) hint = 2\cdot d+random\cdot e \cdot \phi(n)\\ \because a^{\phi(p)}\equiv 1\pmod p, Euler theorem \\ \therefore c^{hint}\equiv c^{2\cdot d}\cdot c^{random\cdot e\cdot \phi(n)}\equiv c^{2\cdot d}\pmod n \\ hint=2⋅d+random⋅e⋅ϕ(n)∵aϕ(p)≡1(modp), o PULL set The reason is ∴chint≡c2⋅d⋅crandom⋅e⋅ϕ(n)≡c2⋅d(modn)
therefore mac = gmpy2.iroot(pow(c,hint,n),2)[0]; Need to know mac The role of
After seeing it again, there are three options ,set key,guess num,get flag
Check the function content separately
def set_key(self, rec):
if self.mac == int(rec[8:]):
self.r = self.counter
It seems to determine whether the input is consistent with mac Agreement , If it's the same , Then perform an assignment operation , See is will counter Assign a value to r
seek counter Generation
def init():
...
counter = random.randint(0, 2**128)
It's just a random number , and self.r The initial value is -1
Why do you want to assign values , Can be in encrypt() Function
def encrypt(self, msg):
msg = self.padding(msg)
if self.r != -1:
self.r += 1
aes = AES.new(self.key, AES.MODE_CTR, counter = Counter.new(128, initial_value=self.r))
return aes.encrypt(msg)
else:
return msg
If self.r If the value of does not change , In other words, there is no set key operation ,AES_CRT The encryption process will not take effect ; If the encryption doesn't work, you can take it directly flag Do you , And then see get flag operation
def get_flag(self, rec):
assert self.r != -1
if self.score == 5:
self.send(flag, enc=False)
else:
self.send(os.urandom(32) + flag)
There is one assert self.r != -1, It means you have to self.r Randomly generated counter Assignment can be performed get flag, Otherwise, it will directly assert Report errors
There is still one of the three options guess num operation
def guess_num(self, rec):
num = random.randint(0, 2**128)
if num == int(rec[10:]):
self.send(b'right')
self.score += 1
else:
self.send(b'wrong')
If you guessed right, the number generated immediately , Is that self.score += 1, and self.score The function is in get flag in
if self.score == 5:
self.send(flag, enc=False)
It means continuous guessing 5 Times can make get flag The operation returns directly to flag
But take a closer look , First of all, the range of random number generation is very large , It's impossible to explode ; Can only guess once , Otherwise you'll be in 6 Waste an opportunity in one choice ; most important of all ,6 One of the choices must be used to set key( Otherwise... Cannot be carried out get flag operation ), Have a chance to get flag, only 4 Second chance , And we need to keep guessing 5 Subrandom number ; therefore guess num Operation now seems to be a cover
So about being able to get flag The only chance to fall is encrypt() On the function , yes AES_CTR encryption , About this model
- The encryption process

As shown in the figure , Introduced a counter CTR, Make exclusive or with each plaintext packet in the second step Encrypted streams Different , Because each encrypted plaintext packet (16 bytes), Counter CTR It will automatically +1
The topic is how to generate CTR Of
from Crypto.Util import Counter
aes = AES.new(self.key, AES.MODE_CTR, counter = Counter.new(128, initial_value=self.r))
It can be seen that Counter.new(128, initial_value=self.r)) in initial_value The variable is set CTR The initial value of the
and CTR The value represented is not simple 00,01, But a group of random number nonce and packet number The initial value of the composition

Each encrypted plaintext packet ,CTR The grouping sequence number will be +1, Cause to proceed encryption The encrypted stream after the operation is completely different from the previous encrypted stream , The byte strings that achieve XOR with each plaintext packet are different from each other
PS: Here and later Encrypted streams All are 
The result of this part ; also Encryption operation especially CTR The operation of the encryptor immediately after generation
- The decryption process
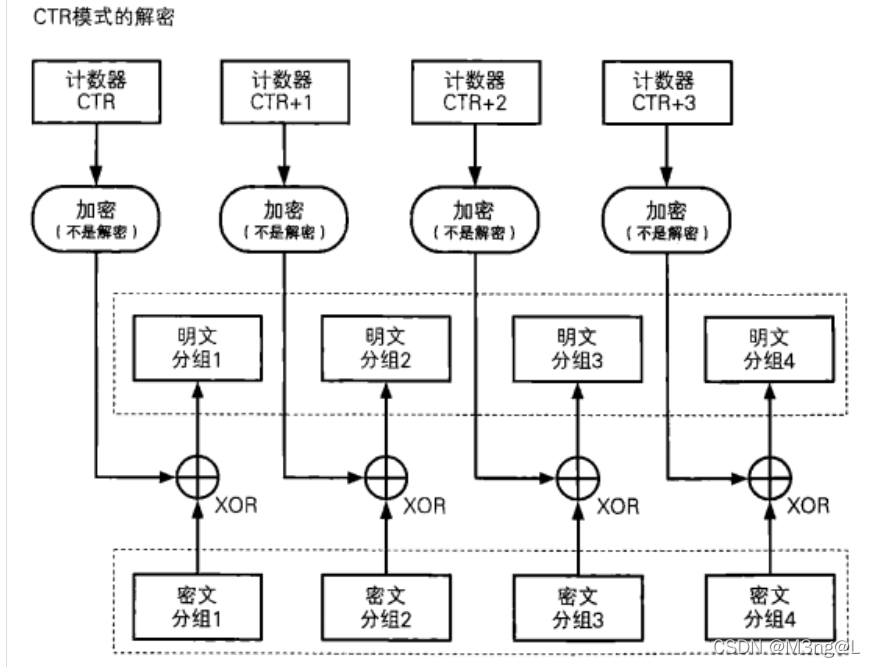
It can be found that resetting the counter CTR Make it generate the same... On the corresponding ciphertext packet as in encryption CTR, Let's do it again encryption operation , Generate the same encrypted stream as in the encryption process , Group XOR with ciphertext to get plaintext group
Analysis finished AES_CTR Encryption and decryption process , It is found that in fact, the encryption and decryption process can be divided into two parts ,CTR encryption and Exclusive or ;
Back to the title script , It's easy to find , Every time the server script send When , Many places in the function are send(x,enc = False), You can find your own defined in the script send function
def send(self, msg, enc=True):
print(msg, end= ' ')
if enc:
msg = self.encrypt(msg)
print(msg, self.r)
self.request.sendall(binascii.hexlify(msg) + b'\n')
The function is to write enc = False Of send In the function , The content will be output directly , That is, in the process of normal interaction send function ; And when enc = True, Or say send There is no right in the function enc Re assign , Then the output content will be encrypt() encryption , That is to say AES_CTR encryption
Careful observation shows that
self.send(b'something wrong, check your input')
# as well as
if num == int(rec[10:]):
self.send(b'right')
self.score += 1
else:
self.send(b'wrong')
there send The function does not actually return plaintext right,something wrong...; It is AES_CTR Encrypted ciphertext ( You can also test locally debug When I found this feature )
It is impossible to encrypt these returned contents for no reason before returning , So this must be breakthrough
Now we can get A pair of Ming ciphertext ,AES_CTR Encrypted flag; Encryption key key Unknown or unknown , Obviously, you can't find the key through normal key To decrypt
A total of 6 Time The opportunity of choice , Then if we get more sets of Ming ciphertext , What's the use
stay AES_CTR Encrypting , If we know the plaintext and the corresponding ciphertext , XOR the two to get Encrypted streams , Because the encryption process
m ⊕ e n c _ s t r e a m = c m\oplus enc\_stream=c m⊕enc_stream=c
The encrypted stream consists of different CTR Generated , If we collect more encrypted streams and splice them together , Then use it and encrypted flag To engage in exclusive or , No, just simulate AES_CTR The decryption process of the pattern
So the final question is which encrypted streams we need , That is, which encrypted streams are encrypted flag Really used when
Of course, the longer the encrypted stream, the better , So we use something wrong... As a ciphertext group, obtain the encrypted stream , Default pass padding The length of the plaintext after the function is 48
Under normal circumstances ( This question is not such a normal situation , It will be mentioned later , It is also one of the key points ) Yes, the encrypted stream should be generated by CTR,CTR+1,CTR+2 Generated , Then it's probably not long enough to match the encrypted flag XOR can get the complete flag( because flag The encryption process is as padding(os.urandom(32)+flag) Encrypted , So the ciphertext will be longer )
Now there is a doubt that if you encrypt two or more times consecutively ,counter Will it automatically continue +1, So that we can actually encrypt different processes ( Although the plaintext is indeed the same ) The multiple encrypted streams generated in are in accordance with CTR+i Stitched together in the order of , As a whole encrypted stream
Practice a
>>> from Crypto.Cipher import AES
>>> from Crypto.Util import Counter
>>> from pwn import *
>>> key = b'\x01' * 16
>>> msg = b"flag1111111111111111111111111111111111111111111111111111111"
>>> t = Counter.new(128, initial_value=123)
>>> aes = AES.new(key, AES.MODE_CTR, counter = t)
>>> enc1 = aes.encrypt(msg)
>>> enc1
b"0=J\xe6\x87\xec\x07r\xf1{L\x94\xf7\xf2\xfcp|-\xf0\xca\xba\xe4:\x89\x7f\rI\xb5\x84\xb8\x00\xe2%(\x02o\xa5\x8c\xa3\x93\x18'\xb0\xa2\xe2\xd4]\xb1*\xb5\x8fH7\xd8\xfa\x8f\x08\xe7X"
>>> enc2 = aes.encrypt(msg)
>>> enc2
b'\x97\xf5\xe3_\xdc\xb3\x1c\x11\x1fM\n\x16\x06}:hvU\x1d\x93"\xf6\x89\xc3\x05\x94\x8b>6ha\xce\'\x9f\xb5$\x07Hm\xa5\xd1]y)P\xff\xd3e\xea\x7f\xa9\xb3\xe9\xcd\x88\x97>\x8d\xad'
Practice has proved that the encrypted streams obtained in different encryption processes can be spliced together , But how to ensure that flag The encrypted stream is consistent with the encrypted stream we obtained , That's reuse set key operation
Roughly repeat, reuse set key The role of
>>> from Crypto.Cipher import AES
>>> from Crypto.Util import Counter
>>> from pwn import *
>>> key = b'\x01' * 16
>>> msg = b"flag1111111111111111111111111111111111111111111111111111111"
>>> t = Counter.new(128, initial_value=123)
>>> aes = AES.new(key, AES.MODE_CTR, counter = t)
>>> enc1 = aes.encrypt(msg)
>>> enc2 = aes.encrypt(msg)
>>> t = Counter.new(128, initial_value=123)
>>> aes = AES.new(key, AES.MODE_CTR, counter = t)
>>> enc3 = aes.encrypt(msg)
>>> enc4 = aes.encrypt(msg)
>>> assert xor(enc1,msg) == xor(enc3,msg)
>>> assert xor(enc2,msg) == xor(enc4,msg)
>>>
It means when we repeat to counter When assigning the same value , Whole CTR The initial value will be refreshed
So do we only need two or three something wrong... The encrypted stream obtained from the ciphertext pair is spliced together with flag Just do XOR
Practice has found that only half of flag, Just before 48 Bit padding(os.urandom(32)+flag); Why is the encrypted stream not corresponding correctly
Find the author in self.r and aes There was a move up there , Before encrypting the whole plaintext every time self.r First of all +1, That is to say CTR + 1; And it will be redefined before encrypting the whole plaintext every time aes = AES.new(self.key, AES.MODE_CTR, counter = Counter.new(128, initial_value=self.r)), This means that for two plaintext ( Not plaintext grouping ) The two used in encryption CTR In the generated encrypted stream , Used by the last set of plaintext grouping of the previous plaintext yes CTR + i, The first group of plaintext grouped by the next plaintext No CTR + i + 1
def encrypt(self, msg):
msg = self.padding(msg)
if self.r != -1:
self.r += 1
aes = AES.new(self.key, AES.MODE_CTR, counter = Counter.new(128, initial_value=self.r))
return aes.encrypt(msg)
else:
return msg
So the encrypted stream in the encryption process is actually CTR + 1,CTR + 2,CTR + 3 Wait, pass encryption Operation generated
And the last plaintext ( Not plaintext grouping ) Encryption involves CTR The initial value is CTR + 1, The next plaintext encryption involves CTR The initial value is CTR + 2( Because every time before encrypting the whole plaintext self.r += 1)
therefore
m 1 : C T R + 1 C T R + 2 C T R + 3 m 2 : C T R + 2 C T R + 3 C T R + 4 m 3 : C T R + 3 C T R + 4 C T R + 5 m_1 : CTR+1~~CTR+2~~CTR+3\\ m_2:CTR+2~~CTR+3~~CTR+4\\ m_3:CTR+3~~CTR+4~~CTR+5\\ m1:CTR+1 CTR+2 CTR+3m2:CTR+2 CTR+3 CTR+4m3:CTR+3 CTR+4 CTR+5
among m i m_i mi yes somgthing srong... In plain text , The above means that the plaintext stream is encrypted before and after CTR + i Generated
In order to make flag Using a known encrypted stream , We use set key Operating handle CTR Refresh , bring
f l a g : C T R + 1 C T R + 2 C T R + 3 C T R + 4 C T R + 5 flag:CTR+1~~CTR+2~~CTR+3~~CTR+4~~CTR+5 flag:CTR+1 CTR+2 CTR+3 CTR+4 CTR+5
So right. m i m_i mi Perform the corresponding interception
S o l v i n g c o d e Solving~code Solving code
from pwn import *
from Crypto.Util.number import *
import gmpy2
import hashlib
import string
import random
import binascii
context.log_level='debug'
io = remote("192.168.109.129","9998")
io.recvuntil(b"+")
tmp = io.recvuntil(b"\n")
part_proof = tmp.split(b") == ")[0]
result = tmp.split(b") == ")[1][:-1]
table = string.ascii_letters + string.digits
while True:
XXXX = ("".join(random.sample(table,4))).encode()
if hashlib.sha256(XXXX + part_proof).hexdigest() == result.decode():
io.recvuntil(b"\n")
io.sendline(XXXX)
break
n = int(binascii.unhexlify(io.recvline()[:-1]))
hint = int(binascii.unhexlify(io.recvline()[:-1]))
c = int(binascii.unhexlify(io.recvline()[:-1]))
mac = gmpy2.iroot(pow(c,hint,n) % n,2)[0]
io.sendline(b"set key:" + str(mac).encode())
enc = []
for _ in range(3):
io.sendline(b"I_want_flag")
time.sleep(0.5)
tmp = io.recvline()[:-1].decode()
if _ != 2:
enc.append(long_to_bytes(int(str(tmp),16))[:16])
else:
enc.append(long_to_bytes(int(str(tmp),16)))
# print(enc)
io.sendline(b"set key:" + str(mac).encode())
time.sleep(0.5)
io.sendline(b"get flag")
time.sleep(0.5)
tmp = io.recvline()
enc_flag = binascii.unhexlify(tmp[:-1])
msg = b'something wrong, check your input'
msg = msg + chr((16 - len(msg)%16)).encode() * (16 - len(msg)%16)
key_stream = b""
for i in enc:
key_stream += xor(i,msg[:len(i)])
print(xor(enc_flag,key_stream[:len(enc_flag)]))
C o n c l u s i o n Conclusion Conclusion
About AES More in-depth topics are interactive , Normally, it is not required to ask for the key key, But the use of xor The characteristics of Encrypting device ( Equivalent to black box encryption ) From the server script Swindle Can be found flag The numerical
When there is no clue about the topic of interaction, it is more likely to interact with the server directly debug return , Instead of just looking at the scripts used by the server
Crypto You need to pay attention to the type of content returned by the server , It is likely that the script will convert decimal values to bytes and then to hexadecimal , Some data processing may be required
版权声明
本文为[M3ng@L]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204212123034300.html
边栏推荐
- 睿智的目标检测50——Tensorflow2 利用mobilenet系列(v1,v2,v3)搭建yolov4目标检测平台
- The programming competition team of Taiyuan University of technology has a bumper harvest in 2022
- 模块三作业 架构设计文档
- Information visualization large screen display board (with download connection)
- Others - interface test by postman
- 红日靶场--内网渗透练习
- Those things about SAP - Career - 36 - from the subject of "fixed assets liquidation"
- 32位电脑和64位电脑
- The annual salary is 170W. Alibaba P8 blind date requires the woman's monthly salary of 10000. Netizen: it's a little high
- 公文管理系统案例展示
猜你喜欢

Information visualization large screen display board (with download connection)

Principal component analysis R language implementation

Sword finger offer 15 Number of 1 in binary

聪明的人脸识别4——Pytorch 利用Retinaface+Facenet搭建人脸识别平台

物联网lora无线数传模块应用案例:LoRawan网关通信技术

Autres - - analyse de la cohérence en double écriture entre redis et MySQL
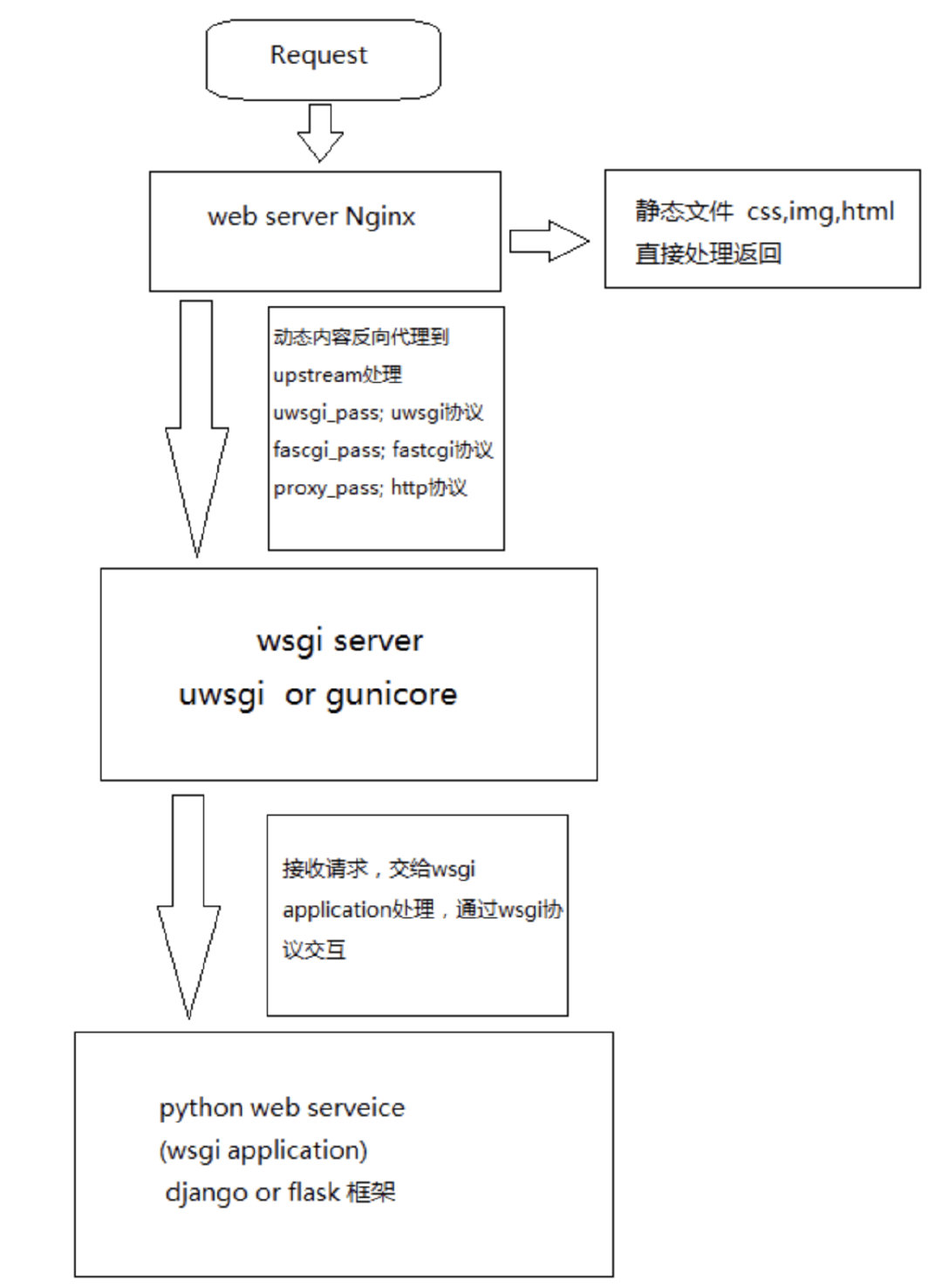
Others - understand CGI, fastcgi, WSGI, uwsgi and uwsgi

其它——CGI,FastCGI,WSGI,uWSGI,uwsgi一文搞懂

其它——DevOps简介
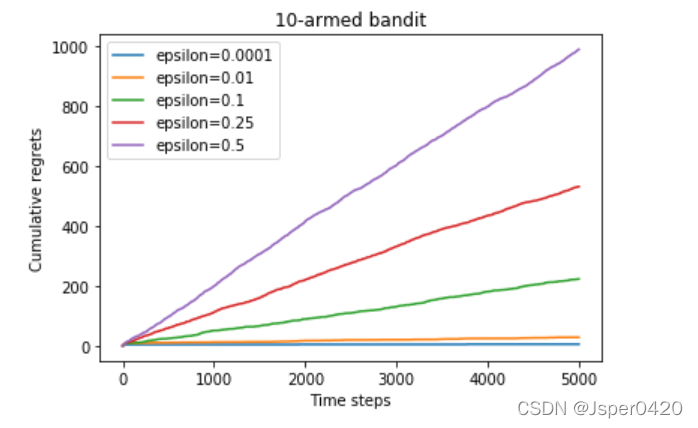
强化学习基础篇(一):多臂老虎机 Multi-armed Bandit
随机推荐
Red sun shooting range -- intranet penetration practice
基于OpenStack的云计算平台搭建
Sword finger offer 15 Number of 1 in binary
[ZigBee wireless communication module step by step] zigbee3 0 module to establish remote network control method
[spark] (task5) fundamentals of sparkml (classification | clustering model)
其它——ZeroRPC和SimpleXMLRPCServer
Kubernetes详解(五)——Kubernetes核心对象
#Reflex WMS研习心得#上架原理
【Selenium 自学系列】(一)Selenium第一个例子及交互原理
工作流引擎 参数设置及业务引擎
Others - Analysis of redis and MySQL double write consistency scheme
其它——Redis与Mysql双写一致性方案解析
Swift uses avplayer and avplayeritem for voice playback
培训管理系统操作说明
841. String hash (string hash template)
two hundred and thirty-two thousand one hundred and thirty-one
读书破万“卷”:国民阅读洞察2022
Bailian4004 数字组合【递归+DP】
L1-005 test seat number
How can urea futures be safe? What are the benefits of urea futures hedging?