Time complexity

There are two ways to evaluate an algorithm , Time and space , However, due to the development of hardware in the computer industry , Space is no longer the main issue we discuss , Time is .
So what is the time complexity ？
Literally , Is the time it takes for an algorithm to run on the machine , In a sense, it's OK, but we have to pay attention to one problem , The hardware level of different machines is different , Compare the running speed of the headmaster's computer with that of our ordinary people's computer , That's not comparable hh,
therefore ： The time taken by an algorithm is proportional to the number of statements executed , The number of times the basic operations in the algorithm are executed , Time complexity of the algorithm
namely ： Find a basic statement and the scale of the problem N Mathematical expressions between , Is to calculate the time complexity of the algorithm .

//  Please calculate Func1 in ++count How many times did the statement execute in total ？
void Func1(int N) 
{
    
int count = 0;
for (int i = 0; i < N ; ++ i)
 {
    
 for (int j = 0; j < N ; ++ j)
 {
    
 ++count;
 }
}// This cycle  N^2
 
for (int k = 0; k < 2 * N ; ++ k)
 {
    
 ++count; // This cycle  2N
 }
int M = 10;
while (M--)
   {
    
      ++count;// This cycle is 10;
   }
 }

According to the above statement , We can get the time complexity function of this algorithm ：
F(N) = N^2+2N+10;
But if the time complexity of each algorithm is calculated like this , That would be too much trouble , Therefore, a concept is introduced —— Progressive time complexity is often seen Big O The progressive representation of .
Before that, let's look at the following discussion
N = 10 F(N) = 130
N = 100 F(N) = 10210
N = 1000 F(N) = 1002010
With N It's getting more and more valuable , The impact of the latter two items on time can be almost ignored
So if you use big 0 Progressive representation The algorithm is O（N^2）;
Then the representation rules are derived ：
1、 With constant 1 Replace all addition constants in the running time, i.e O（1）;
2、 In the modified run times function , Only the highest order terms .
3、 If the highest order term exists and is not 1, The constant multiplied by this item is removed . The result is big O rank .
We can give an example to illustrate what is O（1）

int M = 10;
 while (M--)
 {
    
 ++count;
 }

Because this number is certain , Whether it's 10 still 1000 Or how much , As long as it is a certain number , So time complexity is O（1）;
The rules 2 I have explained above
* Rule three ：
* When the number reaches a certain level ,(N^2)
(2N^2) There should be no difference That's why in daily life , For our convenience , Two time complexities , As long as they have the same highest order , Then let's omit the preceding Arabic numerals directly

long long Fib(size_t N) {
    
 if(N < 3)
 return 1;
 
 return Fib(N-1) + Fib(N-2);
}

This is the famous Fibonacci number
The first thing I learned about recursion was it , But anyone who has learned it knows , This algorithm is not good , After learning the time complexity, we can know that the progressive time complexity of this algorithm is （2^N)
We set each recursion to a unit 1
（ Because the variables in the function are the same So let's assume that a function recursion is 1） But the recursion of each recursion is 2 Multiply sequentially 2 Until the end of recursion Always multiply 2 So the asymptotic time complexity of this algorithm is 2^N;
notes
In addition, some algorithms have the best time complexity 、 Average and worst case ：
The worst ： Maximum number of runs of any input size ( upper bound )
On average ： Expected number of runs of any input size
The best situation ： Minimum number of runs of any input size ( Lower bound )
for example ： At a length of N Search for a data in the array x
The best situation ：1 Times found
The worst ：N Times found
On average ：N/2 Times found
In practice, the general concern is the worst-case operation of the algorithm , Therefore, the time complexity of searching data in the array is O(N)

Spatial complexity

Spatial complexity , Although the evaluation of an algorithm system now accounts for a small proportion , But some algorithm problems still need to be mastered .
First up and down the complexity of space Definition ：
Spatial complexity is also a mathematical expression , It is a measure of the amount of storage space temporarily occupied by an algorithm during operation .
Space complexity is not how much the program takes up bytes Space , Because it doesn't make much sense either , So spatial complexity is the number of variables .
Spatial complexity calculation rules are basically similar to practical complexity , Also use large O Progressive representation .
Be careful ： Stack space required for function runtime ( Store parameters 、 local variable 、 Some register information, etc ) It has been determined during compilation , because
This spatial complexity is mainly applied explicitly by the function at run time Extra space To make sure .
Emphasize the important thing again ！！！ Extra space *

//  Calculation BubbleSort Spatial complexity of ？
void BubbleSort(int* a, int n) {
    
 assert(a);
 for (size_t end = n; end > 0; --end) 
 {
    
 int exchange = 0;
 for (size_t i = 1; i < end; ++i)
 {
    
 if (a[i-1] > a[i])
 {
    
 Swap(&a[i-1], &a[i]);
 exchange = 1;
 }
 }
 if (exchange == 0)
 break;
 }
}

We can see that the complexity of the bubble sorting space above is O（1）;
Only one additional variable is defined exchange
Maybe there is iron son and doubt , This change Variable Every time he creates a loop , Cycle end stack recycle , loop N If time So the spatial complexity is O（N） ah The blogger here quotes a sentence I saw before （ I also forgot where I saw it ）

Time is gone forever , It's cumulative , But space can be reused after recycling ！

I can give a code example to illustrate this problem

long long Fac(size_t N) {
    
 if(N == 0)
 return 1;
 
 return Fac(N-1)*N; }

The complexity of this space is O（N） That's all right.

Well, the following one ？

long long Fib(size_t N) {
    
 if(N < 3)
 return 1;
 
 return Fib(N-1) + Fib(N-2);
}

You may subconsciously think that the complexity of the reaction space is O（N^2） Just like its time complexity

But what I want to tell you is O（N）
Why is this so ？

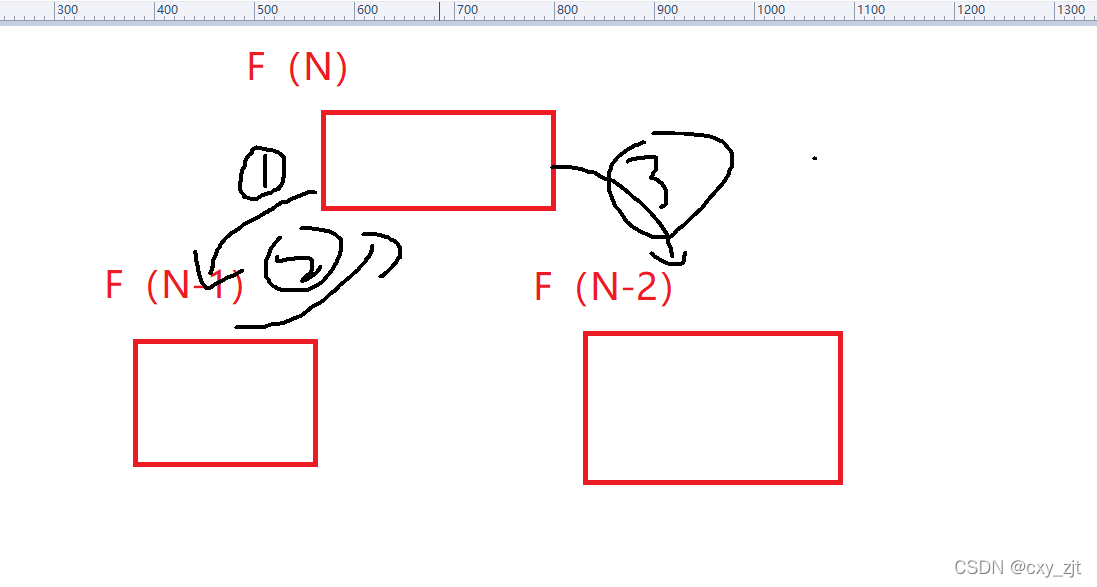
First step First call F（N-1） The stack area opens up space for it But after the call Recycle space Give again F（N-2） Because the stack area opens up the same space for them So the space given to them can be roughly regarded as the same , therefore , Each additional space is 1 instead of 2 So the spatial complexity is O（N）;
Let me give another example to illustrate

because fun1 Function stack frame and fun2 The function stack frame is the same
So we can see that the addresses assigned to them are the same
Function stack frame （ It can be simply understood as the order of the number of variables opened up inside the function ）
Be careful ： Only functions with the same function stack frame can be the same Otherwise it's different ！

The above is my simple analysis of complexity I also hope you can give suggestions below ！