当前位置:网站首页>Deceptive Dice
Deceptive Dice
2022-08-09 23:14:00 【Here_SDUT】
Implication
Give you a dice with n sides, you can roll up to k times, you can stop rolling the dice at any time, and use the last result as your score, the probability of each side of the dice appearing is equal, let you ask forWhat is the expectation to score at most k shots.
Analysis
Let's take a 20-sided dice roll up to 3 times as an example:
Only one throw: the probability of each side is \frac{1}{20}, multiplying the score of each case, you can get: \frac{1}{20} * \sum^{20}_{i= 1}{i} = 10.5
At most two throws: The expectation of one throw is 10.5 points, so the second throw is only performed if the first score is lower than 10.5, so it is divided into one throw and two throws. The expectation of one throw is:\frac{1}{20} * \sum_{i=11}^{20}i, the expectation of two throws can be regarded as the premise that the result of the first throw is 1-10, another throw, i.e. the probability of the first throw being 1-10 times the expectation of only one throw.In summary, the formula is: \frac{1}{20} * \sum_{i=11}^{20}i+\frac{10}{20} * 10.5 = 13
Three throws at most: The expectation of throwing twice is 13, then if the result of the first throw is 1-13, then throwing twice is definitely better, so it can be divided into two situations: the result of the first throwis 14-20, then as long as you vote once, the expectation is: \frac{1}{20} * \sum_{i=14}^{20}i; the first result is 1-13, then you need to continue throwing, which can be regarded as the expectation of throwing at most two times on the basis of the first throwing result of 1-13, namely: \frac{13}{20} * 13
It can be found that each time the result is derived from the previous step, and a recursive relationship can be obtained, then to find the n dice, roll k times as long asIt can be pushed from 1 times to k times. Since the interval sum is used, it can be preprocessed with the prefix sum, and the code implementation is simple.
code
#include #define LL long longusing namespace std;const int maxn = 1e5+10;const int inf = 0x3f3f3f3f;const double PI = acos(-1.0);typedef pair PII;typedef pair PLL;double s[110];LL n, k;int main() {scanf("%lld %lld", &n, &k);for (LL i = 1; i <= n; i++) {s[i] = s[i - 1] + i;}double t = s[n] / n;for (LL i = 2; i <= k; i++) {LLpos = (LL)t;t = (s[n] - s[pos]) / n + (pos)*t / n;}printf("%.8lf\n", t);return 0;} 边栏推荐
- PMP每日一练 | 考试不迷路-8.9(包含敏捷+多选)
- 4D Summary: 38 Knowledge Points of Distributed Systems
- 在VMware上安装win虚拟机
- C语言中的文件是什么?
- 6个规则去净化你的代码
- How to Make Your Company Content GDPR Compliant
- laravel 表迁移报错[通俗易懂]
- The kvm virtual machine cannot be started, NOT available, and the PV is larger than the partition
- LoRa无线技术在物联网应用市场的概况和发展
- 蔚来杯2022牛客暑期多校训练营7 CFGJ
猜你喜欢

【泛型编程】模板全详解
STC8H Development (15): GPIO Drives Ci24R1 Wireless Module
![[Generic Programming] Full Detailed Explanation of Templates](/img/9d/7864f999cb2e4edda2ee7723558135.png)
[Generic Programming] Full Detailed Explanation of Templates

角度和弧度的相互换算

PMP daily practice | didn't lost a 8.9 (including agile + multi-select)
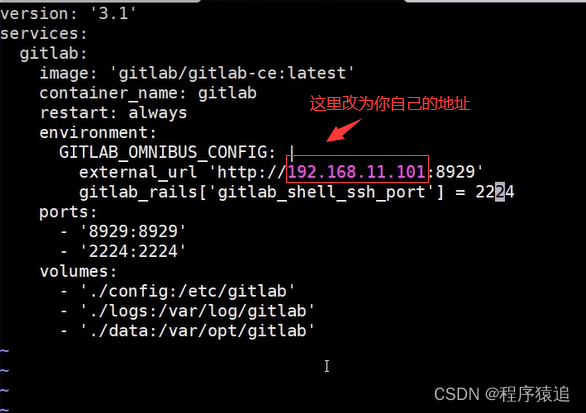
【云原生】4.2 DevOps 精讲篇
别叫我玩,我要考PMP:考PMP选择机构需要了解的那些事儿

Pagoda measurement - building LightPicture open source map bed system

Word文档怎么输入无穷大符号∞
TF generates uniformly distributed tensor
随机推荐
消防安全培训|“蓝朋友”,开课了!
Cookie, session, token
NIO Cup 2022 Nioke Summer Multi-School Training Camp 7 CFGJ
STC8H Development (15): GPIO Drives Ci24R1 Wireless Module
Technology Sharing | How to use the JSON Schema mode of interface automation testing?
PMP每日一练 | 考试不迷路-8.9(包含敏捷+多选)
技术分享 | 接口自动化测试之JSON Schema模式该如何使用?
【云原生】4.2 DevOps 精讲篇
单元测试
【双链表增删查改接口的实现】
random.normal() and random.truncated_normal() in TF
Hessian Matrix 海森矩阵
cadence中复制一部分PCB到另一个PCB中去
宝塔实测-搭建LightPicture开源图床系统
SecureCRT强制卸载
Deceptive Dice(期望计算)
STC8H开发(十五): GPIO驱动Ci24R1无线模块
[corctf 2022] 部分
Install win virtual machine on VMware
How to Make Your Company Content GDPR Compliant