一、The principle of formula derivation

NSubinterpolation basis functions：

 Satisfy the interpolation polynomial

 An interpolating polynomial of the form this formula is calledLagrang插值多项式.

由的定义可知

 If a count is introduced,再求导

因此 

二 、符号说明

输入：

xi：The abscissa of the known data point

k：函数lk(x)的下标k

xx：The abscissa of the point to be interpolated

输出：lk_x,即函数lk(x)在xxThe ordinate of the coordinate point

代码如下：

function li_x = LagrangeFactor( xi, i, xx )
w = 1;
n = length( xi );
syms x;
for j = 1 : n
    w = w * ( x - xi(j) );
end
dw = diff( w );
dwf = matlabFunction( dw );
dwi = dwf( xi(i) );
lx = ( w / ( x - xi(i) ) ) / dwi;
f = matlabFunction( lx );
lk_x = f( xx );
end

• 三、一次插值

1. Preparation of the argument function：

(xi,yi):are the known data point coordinates

代码：xi = [ 0, 1 ];
yi = sin( xi );
n = length( xi );
y = 0;
x = [ xi(1) - 1 : 0.1 : xi(2) + 1 ];

2.根据lagrangeInterpolating polynomial calculationsxThe function value at the coordinate point（纵坐标） 

代码：

for k = 1 : n
    lkx = LagrangeFactor( xi, k, x );
    y = y + yi(k) * lkx;

end

3.绘图 

代码：

figure;
plot( xi, yi, 'b.', 'markersize', 30 )
hold on
plot( x, sin(x), 'k--', 'LineWidth', 1.5  )
plot( x, y, 'r-', 'LineWidth', 2 )
legend( '插值点', '原曲线', 'Interpolate polynomial curves' );
axis( [ -1, 2, -1, 3 ] )

结果如图：

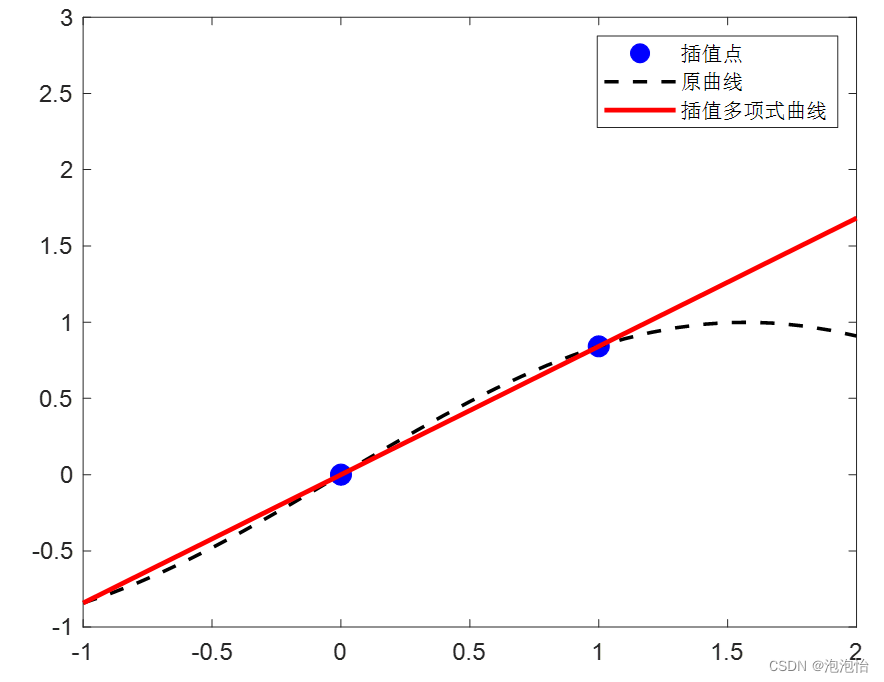
 四、抛物插值

1.Preparation of the argument function：

xi = [ 0, pi/2, pi ];
yi = [ 0, 1, 0 ];
n = length( xi );
y = 0;
x = [ xi(1) - 1 : 0.1 : xi(n) + 1  ];

2.根据lagrangeInterpolating polynomial calculationsxThe function value at the coordinate point

for k = 1 : n
    lkx = LagrangeFactor( xi, k, x );
    y = y + yi(i) * lkx;
end

3.绘图

plot( xi, yi, 'b.', 'markersize', 30 )
hold on
plot( x, sin(x), 'k--', 'LineWidth', 1.5  )
plot( x, y, 'r-', 'LineWidth', 2 )
legend( '插值点', '原曲线', 'Interpolate polynomial curves' );
axis( [ xi(1) - 1, xi(n) + 1, -1, 2 ] )

汇总代码：

clear all
clc
%% 一次插值
%(xi,yi)：
xi = [ 0, 1 ];
yi = sin( xi );
n = length( xi );
y = 0;
x = [ xi(1) - 1 : 0.1 : xi(2) + 1 ];
for k = 1 : n
    lkx = LagrangeFactor( xi, k, x );
    y = y + yi(k) * lkx;
end
%y
figure;
plot( xi, yi, 'b.', 'markersize', 30 )
hold on
plot( x, sin(x), 'k--', 'LineWidth', 1.5  )
plot( x, y, 'r-', 'LineWidth', 2 )
legend( '插值点', '原曲线', 'Interpolate polynomial curves' );
axis( [ -1, 2, -1, 3 ] )
%% 抛物插值
clear all
clc
xi = [ 0, pi/2, pi ];
yi = [ 0, 1, 0 ];
n = length( xi );
y = 0;
x = [ xi(1) - 1 : 0.1 : xi(n) + 1  ];
for k = 1 : n
    lkx = LagrangeFactor( xi, k, x );
    y = y + yi(k) * lkx;
end
%y 
figure;
plot( xi, yi, 'b.', 'markersize', 30 )
hold on
plot( x, sin(x), 'k--', 'LineWidth', 1.5  )
plot( x, y, 'r-', 'LineWidth', 2 )
legend( '插值点', '原曲线', 'Interpolate polynomial curves' );
axis( [ xi(1) - 1, xi(n) + 1, -1, 2 ] )
function lk_x = LagrangeFactor( xi, k, xx )
w = 1;
n = length( xi );
syms x;
for j = 1 : n
    w = w * ( x - xi(j) );
end
dw = diff( w );
dwf = matlabFunction( dw );
dwi = dwf( xi(k) );
lx = ( w / ( x - xi(k) ) ) / dwi;
f = matlabFunction( lx );
lk_x = f( xx );
end