当前位置:网站首页>杭电多校七 1003-Counting Stickmen(组合数学)
杭电多校七 1003-Counting Stickmen(组合数学)
2022-08-10 18:41:00 【AC__dream】
题目: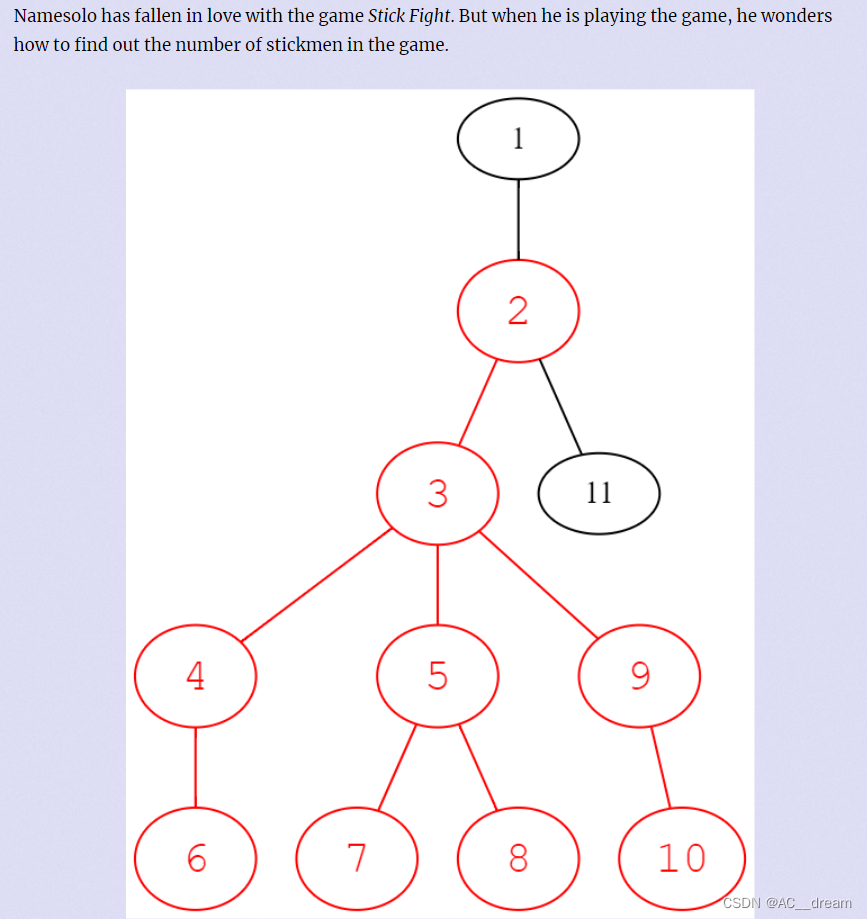

题意:上面标红的部分是一个人,也只有上面这种形状的才算是人,问给定的一棵树中有多少个类似上图的人。
分析:我们能看到3-5这条边算是这个人的腰,因为一个人的腰是唯一的,所以我们可以枚举腰来统计人的个数。对于每一条边u-v,我们都可以假设u是连接腿的节点也可以假设v是连接腿的节点,把两种情况相加即可不重不漏地统计完所有的人。下面我以v作为连接腿的节点来阐述一下如何计算答案:
首先要选择两条边与v有关的边作为腿,而且所选的边还不能包含u-v,那么我们可以用d[i]记录i的度,孩子节点数就是度-1,那么我们脚的选择方案就有(d[i]-1)*(d[i]-2)/2,下面我们来看一下手,手的选择方案计算起来就稍微麻烦一点,首先我们应该从连接头的节点u选择两个长度为2的链作为手,而且这两个长度为2的链要满足两个条件:
(1)不能经过边u-v
(2)不能含有公共部分
我们先不考虑上面两个情况,就是说先看一下从u出发长度为2的链的总条数,其实这个就是u的孩子节点的所有孩子节点和(这里假设节点之间是有父子关系的),这个是比较容易理解的,那经过u-v的长度为2的链有多少呢?因为u-v长度已经是1了,所以我们只需要统计一下从v出发长度为1的且不包含u-v的链有多少就行了,其实也就是v的孩子节点的个数,那么我们用所有的长度为2的链减去经过u-v的长度为2的链就是所有的从u出发的且不经过u-v的长度为2的链的数目,不妨记为t,我们从中任选两个链作为手的方案数就是t*(t-1)/2,但是这样还有一点问题,就是说我们选的两条链虽然都不经过u-v,但是有可能经过同一条边:也就是两个手是这样的情况: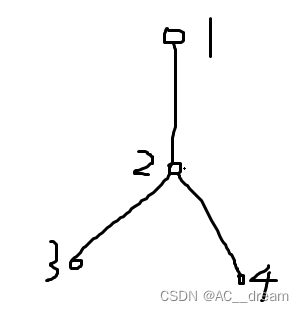
把1-2-3和1-2-4分别看成两个手,这样显然是不符合题意的,我们需要减去这种情况,而这种情况的数目并不是很难计算,比如说j是u的一个孩子节点,那么从j的孩子节点中任选两个都会构成这种情况,所以我们要计算的就是u的所有孩子节点中会构成这种情况的总数目,这个也不难计算,就是C(cnt[j],2)其中j是u的孩子节点,cnt[j]是j的孩子节点,也就是d[j]-1,然后求一个和就行了,需要注意的一点是我们之前没有考虑经过u-v的边,所以这一次考虑u的孩子时也不能考虑v,而为了我们预处理的方便,我们需要先考虑所有孩子节点的边然后最后减去即可。所以我们需要预处理出来![]()
(代码说明:第一个是d[],第二个是f1[],第三个是f2[])
这样我们就处理出来了腿的方案数和手的方案数,头的方案数就更简单了,直接是d[u]-3,因为我们只要选一个长度为1的链,且这条链不能和腰重合,也不能和手重合,所以就是d[u]-3,因为头和手和腰的选取是独立的,所以最后只需要取一个乘积,然后直接对每一条边进行统计答案即可。
细节见代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=5e5+10,mod=998244353;
int h[N],e[N*10],ne[N*10],idx;
void add(int x,int y)
{
e[idx]=y;
ne[idx]=h[x];
h[x]=idx++;
}
int u[N],v[N];
long long d[N],f1[N],f2[N];
//d[i]存储第i个节点的度
//f1[i]存储第i个节点的孩子节点的孩子节点数目和
//f2[i]存储的是第i个节点的孩子节点中选两个孩子的方案数之和
void dfs(int x,int fa)
{
if(fa!=-1)//防止fa为负数时进行数组索引造成越界
{
f1[x]=d[fa]-1;
f2[x]=(d[fa]-1)*(d[fa]-2)/2%mod;
}
else f1[x]=f2[x]=0;
for(int i=h[x];i!=-1;i=ne[i])
{
int j=e[i];
if(j==fa) return ;
dfs(j,x);
f1[x]=(f1[x]+d[j]-1)%mod;
f2[x]=(f2[x]+(d[j]-1)*(d[j]-2)/2%mod)%mod;
}
}
int main()
{
int T;
cin>>T;
while(T--)
{
int n;
scanf("%d",&n);
idx=0;
for(int i=1;i<=n;i++) h[i]=-1,d[i]=0;
for(int i=1;i<n;i++)
{
scanf("%d%d",&u[i],&v[i]);
add(u[i],v[i]);add(v[i],u[i]);
d[u[i]]++;d[v[i]]++;
}
dfs(1,-1);
long long ans=0;
for(int i=1;i<n;i++)
{
long long tv=(d[v[i]]-1)*(d[v[i]]-2)/2%mod;//以v点作为腿的方案数
long long tu=(d[u[i]]-1)*(d[u[i]]-2)/2%mod;//以u点作为腿的方案数
long long sumu=(f1[u[i]]-(d[v[i]]-1))*(f1[u[i]]-d[v[i]])/2%mod;
long long sumv=(f1[v[i]]-(d[u[i]]-1))*(f1[v[i]]-d[u[i]])/2%mod;
ans=(ans+tv*(d[u[i]]-3)%mod*(sumu-(f2[u[i]]-tv)))%mod;
ans=(ans+tu*(d[v[i]]-3)%mod*(sumv-(f2[v[i]]-tu)))%mod;
}
printf("%lld\n",(ans%mod+mod)%mod);
}
return 0;
}边栏推荐
猜你喜欢
[Teach you how to make a small game] Write a function with only a few lines of native JS to play sound effects, play BGM, and switch BGM
什么是企业知识库?有什么作用?如何搭建?
QoS服务质量八拥塞避免

企业即时通讯是什么?可以应用在哪些场景?
钻石价格预测的ML全流程!从模型构建调优道部署应用!

【知识分享】在音视频开发领域中SEI到底是个啥?
剖析Framework面试—>>>冲击Android高级职位

MySQL 查询出重复出现两次以上的数据 - having
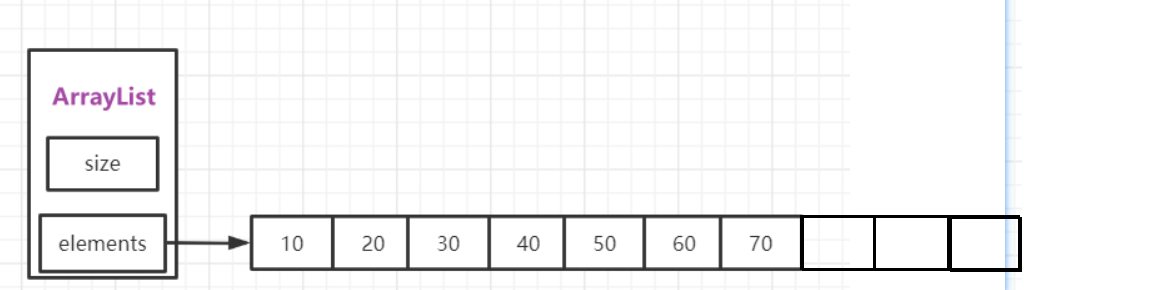
优化是一种习惯●出发点是'站在靠近临界'的地方
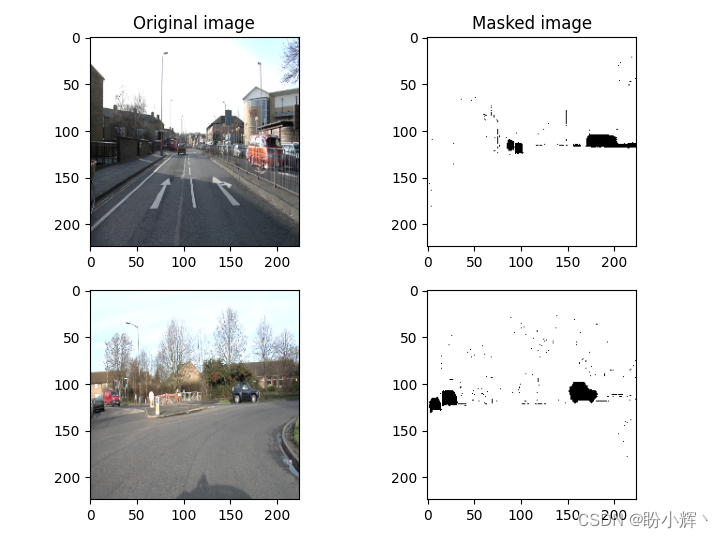
Keras deep learning combat (17) - image segmentation using U-Net architecture
随机推荐
剑指 Offer II 042. 最近请求次数-队列法
关于奉加微PHY62xx系列如何选型?PHY6222/PHY6212/PHY6252
让mixin为项目开发助力【及递归优化新尝试】
宝塔部署flask项目
StoneDB 文档捉虫活动第一季
剖析Framework面试—>>>冲击Android高级职位
谈谈宝石方块游戏中的设计
西安凯新(CAS:2408831-65-0)Biotin-PEG4-Acrylamide 特性
VoLTE基础自学系列 | 3GPP规范解读之Rx接口(上集)
pytorch使用Dataloader加载自己的数据集train_X和train_Y
TikTok选品有什么技巧?
flex&bison系列第一章:flex Hello World
第14章_MySQL事务日志
MSE 治理中心重磅升级-流量治理、数据库治理、同 AZ 优先
Unity_Stack<T>()的应用(多个次级界面后的返回逻辑)
「POJ 3666」Making the Grade 题解(两种做法)
Introduction to 3 d games beginners essential 】 【 modeling knowledge
请问下在datastream中用flinkcdc怎么设置jdbc的参数useSSL=false呀
MySQL 原理与优化:Update 优化
MySQL 查询出重复出现两次以上的数据 - having
![[Teach you how to make a small game] Write a function with only a few lines of native JS to play sound effects, play BGM, and switch BGM](/img/30/714d803d4087f5c9c5800a969055fe)