1 相关概念

1.1 信息熵

信息熵时用来哦衡量信息不确定性的指标，不确定性时一个时间出现不同结果的可能性。
$$H(x)=-\sum _{i=1}^{n}P(X=i)lo{g}_{2}P(X=i)$$
其中：P(X=i)为随机变量x取值为i的概率

1.2 条件熵

条件熵：再给定随机变量Y的条件下，随机变量X的不确定性
$$H(X|Y=v)=-\sum _{i=1}^{n}P(X=i|Y=v)lo{g}_{2}P(X=i|Y=v)$$

1.3 信息增益

信息增益：熵-条件熵。代表了在一个条件下，信息不确定性减少的程度。
$$I(X,Y)=H(X)-H(X|Y)$$

1.4 基尼指数

基尼指数：又称为Gini不纯度，表示在样本集合中一个随机选中的样本杯分错的概率。

注意：Gini指数越小表示集合中被选中的样本被分错的概率越小，也就说集合的纯度越高，反之，集合越不纯。当集合中所有样本为一个类时，基尼指数为0。
$$Gini(p)=\sum _{k=1}^K{p}_k(1-p_k)=1-\sum _{k=1}^K{p}_k$$
其中pk表示选中的样本属于第k个类别的概率。

1.5 集成学习

集成学习是通过构建并组合多个学习器来完成学习任务的算法，集成学习常用的有两类：

Bagging：基学习器之间无强依赖关系，可同时生成的并行化方法

Boosting：基学习器之间存在强烈的依赖关系，必须穿行生成基分类器的方法

（1）Bagging（Bootstrap Aggregating）算法

N个弱学习器，每个学习器的训练数据，来自于原始数据中的随机采样的部分数据。训练模型后，预测新数据。在分类问题中，选择多N个学习器的预测结果中的众数（即，投票方法）作为最终的预测结果。在回归问题中，选择多N个学习器的预测结果中的平均值作为最终的预测结果。

（2）Boosting算法

是将弱学算法提升为强学习算法的过程，通过反复学习得到一系列弱分类器（决策树和逻辑回归）组合这些弱分类器得到一个强分类器。Boosting算法要涉及到两个部分，加法模型和前向分布算法。

加法模型：强分类器由一系列弱分类器线性相加而成。一般组合形式如下：
$$F_M(x:P)=\sum _{m=1}^n{\beta }_{m}h(x;a_m)$$

其中$h(x;a_M)$是弱分类器，$a_m$是弱分类器学习到的最优参数，${\beta }_m$是弱学习在强分类器中所占比重，P是所有$a_m$和${\beta }_m$的组合。这些弱分类器线性相加组成强分类器。

前向分步：在训练过程中，下一轮迭代产生的分类器是在上一轮的基础上训练得来的。
$$F_m(x)=F_{m-1}(x)+{\beta }_m{h}_m(x;a_m)$$

2 随机森林

（1）概念

随机森林 = Bagging+决策树

同时训练多个决策树，预测试综合考虑多个结果进行预测，例如取多个节点的均值（回归问题），或者众数（分类）。

（2）优缺点

优点

1. 它可以出来很高维度（特征很多）的数据，并且不用降维，无需做特征选择
2. 它可以判断特征的重要程度
3. 可以判断出不同特征之间的相互影响
4. 消除了决策树容易过拟合的缺点
5. 减小了预测的方差，预测值不会因训练数据的小变化而剧烈变化
6. 训练速度比较快，容易做成并行方法
7. 实现起来比较简单
8. 对于不平衡的数据集来说，它可以平衡误差。
9. 如果有很大一部分的特征遗失，仍可以维持准确度。

缺点

1. 随机森林已经被证明在某些噪音较大的分类或回归问题上会过拟合。
2. 对于有不同取值的属性的数据，取值划分较多的属性会对随机森林产生更大的影响，所以随机森林在这种数据上产出的属性权值是不可信的

（3）随机性体现在两点

• 从原来是训练数据集随机（带放回Boostrap）取一个子集，作为森林中某一个决策树的训练数据集
• 每一次选择分叉的特征时，限定为在随机选择的特征的子集中寻找一个特征

3 AdaBoost

（1）概念

AdaBoost的思想时将关注点放在被错误分类的样本上，减小上一轮被正确分类的样本权值，提高被错误分类的样本权值。

Adaboost采用加权投票的方法，分类误差小的弱分类器的权重大，而分类误差大的弱分类器的权重小。

（2）算法过程

假设输入的训练数据为：
$$\begin{gathered} T=\{(x_1,y_1),(x_1,y_1),...,(x_N,y_N)\} \\ {x}_i\in X\subseteq R^n,y_i\in Y=\{-1,1\} \end{gathered}$$
迭代次数即弱分类器个数M

1. 初始化训练样本的权值分布为
   $$D_1=(w_{1,1},w_{1,2},...,w_{1,i})=\frac{1}{N},i=1,2,..,N$$

2. 对于m = 1,2,…,M

   （a）使用具有权值分布$D_m$的训练数据集进行学习，得到弱分类器$G_m(x)$

   （b）计算$G_m(x)$在训练集上的分类误差率
   $$e_m=\sum _{i=1}^N{w}_{m,i}I(G_m(x_i)\ne y_i)$$
   （c）计算$G_m(x)$在分类器中所占的权重
   $${\alpha }_m=\frac{1}{2}log(\frac{1-e_m}{e_m})$$
   （d）更新训练数据集的权值分布（这里，$z_m$时归一化因子，为了使得样本的概率分布和为1）：
   $$\begin{gathered} w_{m+1,i}=\frac{w_{m,i}}{z_m}exp(-{\alpha }_m{y}_i{G}_m(x_i)),i=1,2,...,10 \\ {z}_m=\sum _{i=1}^N{w}_{m,i}exp(-{\alpha }_m{y}_i{G}_m(x_i) \end{gathered}$$

   3. 得到最终的分类器为：
      $$F(x)=sign(\sum _{i=1}^N{\alpha }_m{G}_m(x))$$

4 GBDT

（1）BDT提升树概念

BDT提升树：是以CART决策树为基学习器的集成学习方法。实际上就是加法模型和前向分布算法
$$\begin{gathered} f_0(x)=0,初始化提升树 \\ {f}_m(x)=f_{m-1}+T(x,{\theta }_m)，迭代m次，包含m棵决策树的提升树 \\ {f}_M=\sum _{m=1}^{M}T(x,{\theta }_m)，包含m棵决策树的提升树 \end{gathered}$$
在前向分布算法第m步时，给当前的模型$f_{m-1}(x)$求解，最小化损失函数：
$$min(\sum _{i=1}^{N}L(y_i,f_{m-1}(x)+T(x,{\theta }_m))$$
得到第m棵决策树$T(x,{\theta }_m)$。不同问题的提升树的区别在于损失函数的不同，如分类用指数损失函数，回归使用平方误差损失。

当提升树采用平方损失函数时，第m次迭代时表示为
$$\begin{gathered} L(y,f_{m-1}(x)+T(x,{\theta }_m))=(y-f_{m-1}(x)-T(x,{\theta }_m){)}^2 \\ =(r-T(x,\theta ){)}^2 \end{gathered}$$
称r为残差，所以第m棵决策树$T(x,{\theta }_m)$是对该残差的拟合。要注意的是提升树算法中的基学习器CART树是回归树。

（2）提升树算法

（3）GBDT算法概念

GBDT（Gradient Boosting Decision Tree）梯度提升决策树，理解为梯度提升+决策树。利用最速下降的近似方法，利用损失函数的负梯度拟合基学习器。
$$-[\frac{\partial L(y_i,F(x_i))}{\partial F(x_i)}{]}_{F(x)=F_{t-1}(x)}$$
怎么理解这个近似呢，我们通过平方损失函数来推导一下。

为了方便求导，在损失函数前面乘以1/2
$$L(y_i,F(x_i))=\frac{1}{2}(y_i-F(x_i){)}^2$$
对$F(x_i)$求导，则有
$$\frac{\partial L(y_i,F(x_i))}{\partial F(x_i)}=F(x_i)-y_i$$

得到残差与负梯度的关系，即残差是梯度的相反数：
$$r_{ti}=y_i-F_{t-1}(x)=-[\frac{\partial L(y_i,F(x_i))}{\partial F(x_i)}{]}_{F(x)=F_{t-1}(x)}$$
所以在GBDT中使用负梯度替代BDT中的残差进行拟合

（4）GBDT的梯度提升过程

（5）GBDT是算法过程图

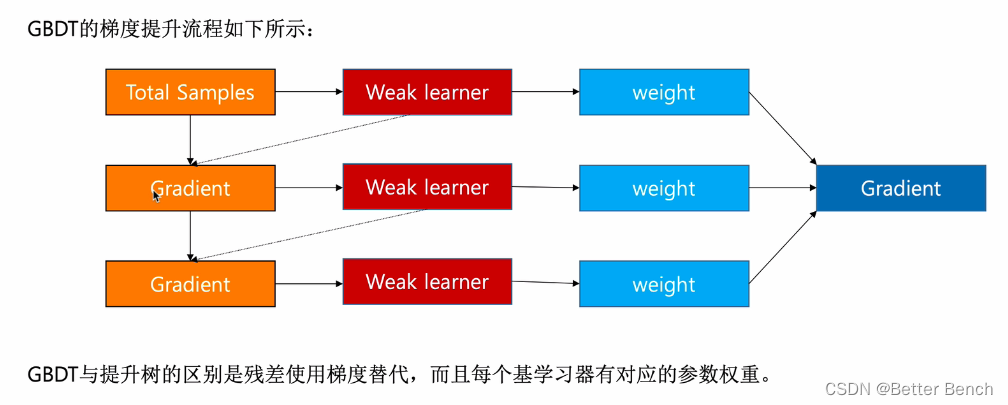
每次更新梯度让下一个弱学习器来学习。

（6）回归问题中，GBDT算法过程

基学习器是CART回归树，CART回归树是将空间内划分为K个不相交的区域，并确定每个区域的输出ck，数学表达式如下：
$$f(X)=\sum _{k=1}^K{c}_{k}I(X\in R_k)$$
则GBDT应用到回归问题的算法过程如下

（7）分类问题中，GBDT仍然使用CART回归树作为基学习器，使用Softmax进行概率的映射，然后对概率的残差进行拟合。所以算法过程如下。

（8）举例理解

GDBT在三个类别的分类问题中

5 XGBoost

（1）基本基本概念

XGBoost是GBDT的一种，也是加法模型和前向优化算法。

在监督学习中，可以分为：模型，参数，目标函数和学习方法。

• 模型：给定输入x后预测输出y的方法，比如说回归，分类，排序等
• 参数：模型中的参数，比如线性回归中的权重和偏置
• 目标函数：即损失函数，包含正则化项
• 学习方法：给定目标函数后求解模型和参数的方法，比如：梯度下降法，数学推导等。

这四个方面的内容，也指导着XBGBoost系统的设计。

（2）XGB的模型形式

给定数据集
$$D=(X_i,y_i)(|D|=n,x_i\in R^m,y_i\in R)$$
XGB利用前向分布算法，学习到包含K棵树的加法模型：
$$\widehat{y_i}=\sum _{i=1}^K{f}_t(x_i),f_t\in F$$
其中有K棵树，f是回归树，而F对应回归树组成的函数空间，那么怎么得到这些树呢，也就是树的结构和叶子节点的预测结果怎么得到？

（2）XGB的目标函数

定义目标函数，包含正则项
$$Obj(\theta )=\sum _{i=1}^{N}l(y,{\hat{y}}_i)+\sum _{j=1}^t\Omega (f_i),f_j\in F$$
如何优化这个目标函数呢，因为f是决策树，而不是数值型的向量，我们不能使用梯度下降的算法进行优化。因此将损失函数进行改写后，利用贪心算法寻找局部最优解。
$${\hat{y}}_i^t=\sum _{j=1}^t{f}_j(x_i)={\hat{y}}_t^{t-1}+f_t(x_i)$$
每一次迭代我们寻找是使得损失函数降低最大的f（CART树），因此目标函数可改写为：
$$\begin{gathered} Ob{g}^{(}t)=\sum _{i=1}^{N}l(y,{\hat{y}}_i)+\sum _{j=1}^t\Omega (f_i) \\ =\sum _{i=1}^{N}l(y_i,{\hat{y}}^{(t-1{)}_t}+f_t(x_i))+\Omega (f_{t}t)+constant \\ =\sum _{i=1}^{N}l(y_i,{\hat{y}}_i^{(t-1)}+f_t(x_i))+\Omega (f_t) \end{gathered}$$
在t轮时，前t-1次迭代，正则项看作是常熟，即constant表示。

要求解以上局部最优解，引入泰勒展开式。

泰勒公式：假设$x^{t+1}=x^t+\Delta x$，将$f(x^{t+1})$处的泰勒展开为：
$$f(x^{t+1})=f(x^t)+f^1(x^t)\Delta x+\frac{f^2(x^t)}{2}\Delta x^2+...$$

接下来采用泰勒展开对目标参数进行近似：
$$\begin{gathered} =\sum _{i=1}^{N}l(y_i,{\hat{y}}_i^{(t-1)}+f_t(x_i))+\Omega (f_t) \\ =\sum _{i=1}^N(l(y_i,{\hat{y}}_i^{t-1})+g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i))+\Omega (f_t) \\ {g}_i=\frac{\partial l(y_i,\widehat{(}y{)}_i^{(t-1)})}{\partial {\widehat{y_i}}^{(t-1)}} \\ {h}_i=\frac{{\partial }^{2}l(y_i,{\hat{y}}_i^{(t-1)})}{{\partial }^2{\hat{y}}_i^{(t-1)}} \end{gathered}$$
移除对第t轮迭代来说的常数项$l(y_i,{\widehat{y_t}}^{(t-1)})$得到：
$$Ob{j}^{(t)}=\sum _{i=1}^N(g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i))+\Omega (f_t)$$
所以目标函数只依赖每条数据在误差函数的一阶导数和二阶导数。

XGB中正则项用来表示树的复杂度：树的叶子节点个数T和每棵树的叶子节点输出分数W的平方和（相当于L2正则化）
$$\Omega (f_t)=\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{\omega }_j^2$$
其中T为叶子节点个数，${\omega }_j$为叶节点的输出，$\lambda$是常熟。

则目标函数改写为

上面式子中第一部分是对样本的累加，而后面部分是正则项，即对叶子节点的累加。

定义q函数将输入x映射到某个叶子节点上，则有：
$$f_t(x)=w_{q(x)},w\in R^T,q:R^d\to \{1,2,..,T\}$$

则目标函数进一步改写为：
$$\begin{gathered} Ob{j}^{(t)}=\sum _{i=1}^N(g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i))+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{\omega }_j^2 \\ =\sum _{i=1}^N(g_i{w}_{q(x_i)}+\frac{1}{2}{h}_i{w}_{q(x_i)}^2)+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2 \\ =\sum _{j=1}^T(\sum _{i\in I_i}{g}_i{w}_j+\frac{1}{2}\sum _{i\in I_j{w}_j^2})+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2 \\ =\sum _{j=1}^T(G_j{w}_j+\frac{1}{2}(H_j+\lambda )w_j^2)+\gamma T \\ {G}_j=\sum _{i\in I_j}{g}_t,H_j=\sum _{i\in I_j}{h}_j \end{gathered}$$
得到最终的目标函数。

（3）优化目标函数

接下来我们继续目标函数的优化，即计算第t轮时使得目标函数最小的叶节点的输出分数w。直接对w求导，使得导数为0，得到
$$w_j=\frac{G_j}{H_j+\lambda }$$
将其带入损失函数中，得到损失函数
$$Ob{j}^{(t)}=-\frac{1}{2}\sum _{j=1}^T(\frac{G_j^2}{H_j+\lambda })+\gamma T$$
所以目标函数中，$\frac{G_j^2}{H_j+\lambda }$越小，目标函数越小。

注意，这里的Gj和Hj来自于损失函数的泰勒展开的一阶梯度和二阶梯度。
$$\begin{gathered} g_i=\frac{\partial l(y_i,\widehat{(}y{)}_i^{(t-1)})}{\partial {\widehat{y_i}}^{(t-1)}} \\ {h}_i=\frac{{\partial }^{2}l(y_i,{\hat{y}}_i^{(t-1)})}{{\partial }^2{\hat{y}}_i^{(t-1)}} \\ {G}_j=\sum _{i\in I_j}{g}_t \\ {H}_j=\sum _{i\in I_j}{h}_j \end{gathered}$$

（4）计算目标函数的例子

（5）XGBoost的学习策略

采用贪心算法，每次尝试分裂一个叶节点，计算分裂后的增益，选择增益最大的，类似于ID3中的信息增益，和CART树中 基尼指数。那XGB中怎么计算增益呢？损失函数是
$$Ob{j}^{(t)}=-\frac{1}{2}\sum _{j=1}^T(\frac{G_j^2}{H_j+\lambda })+\gamma T$$
其中$\frac{G_j^2}{H_j+\lambda }$衡量了叶子节点对总体损失的贡献，因为目标函数越小越好，则$\frac{G_j^2}{H_j+\lambda }$越大越好，在XGB中的增益计算方法是：

Gain值越大，说明分裂后能使目标函数减小的越多，也就是越好。

一般树结构的及确定，初期采用精确贪心算法，就像CART树一样，枚举所有的特征和特征值，计算树的分裂方式。

但精确贪心算法优缺点，当数据量庞大，无法全部存入内存中，精确算法就很慢，因此引入近似算法。根据特征k的分布确定l个候选切分点$S_k=\{s_{k1},s_{k2},...,s_{kl}\}$，然后根据候选切分点把相应的样本放入对应的桶中，对每个桶的G，H进行累加，在候选切分点集合上进行精确贪心查找。算法过程如下：

近似算法根据分位数给出对应的候选切分点，例子如下：

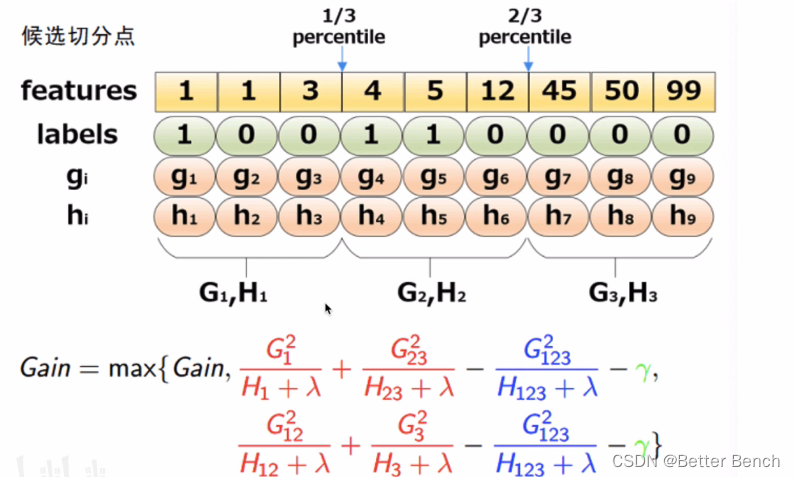
近似算法中如何选取切分点？全局策略和局部策略又是什么？

全局策略：学习每棵树前，提出候选的切分点，当切分点数足够多时，和精确的贪心算法性能相当。

局部策略：树节点分割时，重新提出候选切分点，切分点个数不需要那么多，性能与精确贪心算法差不多。

XGB并没有采用简单的分位数方法，而是提出以二阶梯度h为权重的分位数算法（Weighted Quantile Sketch），对特征k构造muti-set的数据集。
$$D_k=(x_{1k},h_1),(x_{2k},h_2),...,(x_{nk},h_n)$$
其中，$x_{ik}$表示样本i的特征k的取值，而$h_i$是对应的二阶梯度。定义一个rank function ，表示第k个特征小于z的样本比例。
$$r_k(z)=\frac{1}{{\sum }_{(xh)\in D_k}h}\sum _{(x,h)\in D_k,x<z}h$$
切分点$ {s_{k1},s_{k2},…,s_{kl}$应满足：
$$|r_k(s_{k,j})-r_k(s_{k,j+1})|<ϵ,s_{k1}=mi{n}_i{x}_{ik},s_{kl}=ma{x}_i{x}_{ik}$$
也就是说相邻的两个候选切分点相差不超过某个值$ϵ$

稀疏值处理：稀疏值产生的原因时，数据缺失值，大量的零值，One-hot编码。

XGB能对缺失值自动进行处理，思想是对于缺失值自动学习出它该划分的方向。简单来说，三个步骤：

第一步：将特征k的缺失值都放在右子树，枚举划分点，计算最大的增益

第二步：将特征k的缺失值都放在左子树，枚举划分点，计算最大的增益

第三步：最后求出最大增益，确定缺失值的划分

在XGB中加入了步长$\eta$，也叫做收缩率Shrinkage:
$${\hat{y}}_i^t={\hat{y}}_i^{(t-1)}+\eta f_t(x_i)$$
这有助于防止过拟合，通常取值为0.1

列采用技术：一种是按层随机采样，另一种是按树随机采样（构建树前就随机选择特征）

按层随机方式：在每次分裂一个节点的时候，对同一层内的每一个节点分裂之间，先随机选择一部分特征，这时只需要遍历一部分特征，来确定最后分割点。

按树随机方式：即构建树结构前就随机选择特征，之后所有叶子节点的分裂都只只用这部分特征。

（6）XGB的系统设计

分块并行：在建树的过程中，最耗时的是找最优的切分点，而这个过程中，最耗时的部分是将数据排序。见了减少排序的时间，提出Block结构存储数据。

• Block中的数据以稀疏格式CSC进行存储
• Block中的特征进行排序（不对缺失值排序）
• Block中特征害需要存储指向样本的索引，这样才能根据特征的值来取梯度。
• 一个Block中存储一个或多个特征的值。

只需在建树前排序一次，后买你节点分裂时可以直接根据索引得到梯度信息。

• 在精确算法中，将整个数据集存放在一个Block中，这样，复杂度从原来的$O(Hd||x||0logn)$将为$O(Hd||x||0+||x||0logn)$，其中$||x|{|}_0$为训练集中非缺失值的个数。这样，就省去了每一步中的排序开销。
• 在近似算法中，使用多个Block，每个Block对应原来数据的子集。不同的Block可以在不同的机器上计算。该方法对Local策略尤其有效，因为Local策略每次分支都重新生成候选切分点。

缓存优化：使用Block结构的缺点时取梯度的时候，时通过索引来获取的额，而这些梯度的获取顺序时按照特征大小顺序的。这将导致非连续的内存访问，可能使CPU cache缓存命中率低，从而影响算法效率。

对于精确算法中，使用缓存预取。具体来说，对每个线程分配一个连续的Buffer，读取梯度信息并存入Buffer中（这样就实现了非连续到连续的转化），然后再统计梯度信息。该方式再训练样本数大的时候特别有用。

再近似算法中，对Block的大小进行了合理的设置。定义Block的大小为Block中最多的样本数。设置合适的大小时重要的，设置过大则容易导致命中率低，过小容易导致并行化效率不高。

Out of core Computation：当数据量太大不能全部不放入主内存的时候，为了使得out of core 计算称为可能，将数据划分为多个Block并存放在磁盘上。

• 计算的时候，使用独立的线程预先将Block放入主内存，因此可以在计算的同时读取磁盘。

• Block压缩

• Block Sharding，将数据划分到不同磁盘上，提高磁盘吞吐率