当前位置:网站首页>数论之拓展欧几里得
数论之拓展欧几里得
2022-04-23 06:21:00 【Zimba_】
概要:
首先来看它进化前的样子,也就是人尽皆知的欧几里得算法,用辗转相除法求gcd。
ll gcd(ll a,ll b)
{
return b?gcd(b,a%b):a;
}
而拓展欧几里得,则是在欧几里得算法的应用上进行了拓展。它在求解gcd的基础上,额外解决了一个问题——求解二元不定方程的通解,即 a x + b y = m ax+by=m ax+by=m,其中 a a a, b b b, m m m为已知, x x x, y y y为未知量,要求解 x x x和 y y y的解。
正文:
首先,要满足方程有解的充要条件: [ ( a , b ) ∣ m ] [(a,b)|m] [(a,b)∣m]。
如果不满足,则方程无解。
ps: ( a , b ) (a,b) (a,b)表示 a a a和 b b b的最大公约数,而 ∣ | ∣是整除符号,也就是 m m m是 g c d ( a , b ) gcd(a,b) gcd(a,b)的倍数。这个我也不知道怎么证,可以算是易得吧,读者自行思考。
于是乎,原方程可以看成这样, a x + b y = t × g c d ( a , b ) ax+by=t \times gcd(a,b) ax+by=t×gcd(a,b)。
可以发现,我们只要求出 a x + b y = g c d ( a , b ) ax+by=gcd(a,b) ax+by=gcd(a,b)的解,然后将其乘上 t t t即可。
重点来了!!!
首先我们要求一组特解。
我们递归将 a a a和 b b b进行辗转相除法,到递归边界时, a = g c d ( a , b ) , b = 0 a=gcd(a,b),b=0 a=gcd(a,b),b=0。
此时方程 g c d ( a , b ) x + 0 ∗ y = g c d ( a , b ) gcd(a,b)x+0*y=gcd(a,b) gcd(a,b)x+0∗y=gcd(a,b)的一组解我们可以轻松得到: x = 1 , y = 0 x=1,y=0 x=1,y=0。
我们从上一级的 a a a和 b b b变到下一层的 a a a和 b b b后,方程的解也从上一层的 x x x和 y y y变成了下一层的 x x x和 y y y。所以我们在递归回溯的同时,通过下层的 x x x和 y y y来计算得到上一层的 x x x和 y y y。(具体步骤略)
于是,我们得到了方程的一组特解 x 0 × t x_{0} \times t x0×t, y 0 × t y_{0} \times t y0×t。
于是,我们又得到了方程的通解 x = x 0 t + k b g c d ( a , b ) , y = y 0 t − k a g c d ( a , b ) x=x_{0}t+\frac{kb}{ gcd(a,b) },y=y_{0}t-\frac{ka}{ gcd(a,b) } x=x0t+gcd(a,b)kb,y=y0t−gcd(a,b)ka。
模板:
ll ex_gcd(ll a,ll b,ll& x,ll& y)
{
if(b==0)
{
x=1;y=0;
return a;
}
ll g=ex_gcd(b,a%b,x,y);
ll tmp=x;
x=y;
y=tmp-a/b*y;
return g;
}
应用(exgcd求逆元):传送门
关于逆元,也就是 a − 1 a^{-1} a−1,这里不详细介绍了。
a在模p意义下逆元存在的充要条件: [ g c d ( a , p ) = 1 ] [gcd(a,p)=1] [gcd(a,p)=1]
当模数p为质数时,可以利用费马小定理: a p − 1 ≡ 1 ( m o d p ) a^{p-1}\equiv 1\; (mod \; p) ap−1≡1(modp)
我们要求 a x ≡ 1 ( m o d p ) ax\equiv 1\; (mod \; p) ax≡1(modp),此时 x x x只要等于 a p − 2 a^{p-2} ap−2就好了。
然后当模数p不为素数时,那就是拓展欧几里得啦。
要求解 a x ≡ 1 ( m o d p ) ax\equiv 1\; (mod \; p) ax≡1(modp)。其实就是求解 a x + p y = 1 ax+py=1 ax+py=1的一组特解。恍然大悟,后面就不说了。
模板(拓欧求逆元):
ll ex_gcd(ll a,ll b,ll& x,ll& y)
{
if(b==0)
{
x=1;y=0;
return a;
}
ll ans=ex_gcd(b,a%b,x,y);
ll tmp=x;
x=y;
y=tmp-a/b*y;
return ans;
}
ll inv(ll a,ll mod)//存在逆元条件:gcd(a,mod)=1
{
ll x,y;
ll g=ex_gcd(a,mod,x,y);
if(g!=1)return -1;
return (x%mod+mod)%mod;
}
版权声明
本文为[Zimba_]所创,转载请带上原文链接,感谢
https://blog.csdn.net/weixin_43785386/article/details/104084294
边栏推荐
猜你喜欢

北峰通信助力湛江市消防支队构建PDT无线通信系统

How to improve the service efficiency of the hotel without blind spots and long endurance | public and Private Integrated walkie talkie?

可视化常见问题解决方案(九)背景颜色问题

Patrol inspection intercom communication system in power industry

可视化常见绘图(五)散点图

Beifeng communication helps Zhanjiang fire brigade build PDT wireless communication system

USO technology was invited to share the technical framework and challenges of AI synthetic virtual characters at lvson2020 conference

Take you to travel in space, and American photography technology provides comprehensive technical support for aerospace creative applet

The people of Beifeng have been taking action
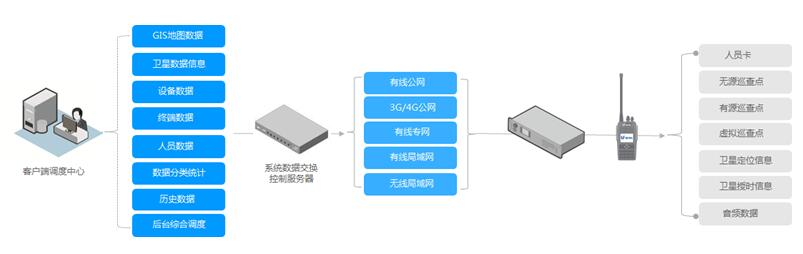
SDC intelligent communication patrol management system of Nanfang investment building
随机推荐
remote: Support for password authentication was removed on August 13, 2021.
el-table 横向滚动条固定在可视窗口底部
菜菜的并发编程笔记 |(九)异步IO实现并发爬虫加速
H5案例开发
Beifeng communication helps Zhanjiang fire brigade build PDT wireless communication system
地铁无线对讲系统
Intelligent communication solution of Hainan Phoenix Airport
Lead the industry trend with intelligent production! American camera intelligent video production platform unveiled at 2021 world Ultra HD Video Industry Development Conference
数据分析学习(一)数据分析和Numpy基础
自定义钉钉机器人进行报警
Solution of wireless intercom system in Commercial Plaza
Warning "force fallback to CPU execution for node: gather_191" in onnxruntime GPU 1.7
LATEX使用
各类日期转化的utils
字节跳动2020秋招编程题:根据工号快速找到自己的排名
VScode
记录一个查询兼容性的网站,String.replaceAll()兼容性报错
使用compressorjs压缩图片,优化功能,压缩所有格式的图片
在项目中的定时作用
Wireless communication system for large-scale sports events