当前位置:网站首页>Complexité temporelle et spatiale
Complexité temporelle et spatiale
2022-04-22 05:19:00 【Poisson de fond】
Catalogue des articles
Préface
Ce chapitre traite des questions liées à la complexité temporelle et spatiale,Analyse principalement à l'aide d'exemples communs,Cycle、Récursion、Fibonacci、Factoriel、Tri des bulles、Recherche binaire, etc..
Un.、Efficacité de l'algorithme
Après avoir écrit l'algorithme comme exécutable,Le temps d'exécution exige des ressources en temps et en espace qui mesurent généralement la qualité d'un algorithme,La complexité temporelle est généralement mesurée à partir de deux dimensions, le temps et l'espace, qui mesurent principalement la vitesse et la lenteur d'un algorithme,Et la complexité spatiale mesure principalement l'espace supplémentaire nécessaire au fonctionnement d'un algorithme.Mais avec le développement des ordinateurs,La capacité de stockage a atteint un niveau élevé,Nous ne sommes donc pas très préoccupés par la complexité spatiale,Souvent, l'espace change de temps.
2.、Complexité temporelle
1.Définition de la complexité temporelle
En informatique,La complexité temporelle de l'algorithme est une fonction.Il décrit quantitativement le temps de fonctionnement de l'algorithme.Le temps qu'il faut pour exécuter un algorithme,En théorie,,On ne peut pas compter,Il n'y a que vous qui lancez le programme sur la machine,Pour savoir.Mais devons - nous tester chaque algorithme?Ce n'est pas trop gênant,C'est pour ça qu'il y a cette méthode d'analyse de la complexité temporelle. Le temps qu'un algorithme prend est proportionnel au nombre de fois qu'il est exécuté , Nombre d'opérations de base effectuées dans l'algorithme ,Est la complexité temporelle de l'algorithme.
2.Représentation de la complexité temporelle
Nous utilisons généralement de grandes O Représentation asymptotique description la complexité temporelle est simple à dire 0La notation est, L'ordre le plus élevé du nombre d'opérations calculées .
En général, nous nous concentrons sur le pire fonctionnement de l'algorithme .
3.FAQ analyse de la complexité temporelle
void test1(int N)
{
int count = 0;
for (int k = 0; k < 2 * N; ++k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}
Mise en œuvre2*N+10Une fois,Complexité temporelleO(N)
void test2(int M,int N)
{
int count = 0;
for (int k = 0; k < M; ++k)
{
++count;
}
for (int k = 0; k < N; ++k)
{
++count;
}
printf("%d\n", count);
}
Complexité temporelleO(M+N)
void test3(int N)
{
int count = 0;
for (int k = 0; k < 100; ++k)
{
++count;
}
printf("%d\n", count);
}
Complexité temporelleO(1)(Mise en œuvre100Une fois)
long long Fib(size_t N)
{
if (N < 3)
return 1;
return Fib(N - 1) + Fib(N - 2);
}
C'est une série Fibonacci , La complexité temporelle est énorme O(2^N)
Cet algorithme n'a en fait qu'un sens théorique , Ça n'a guère de sens , La complexité de l'algorithme est trop grande
Il y a beaucoup de façons de remplacer ça , Par exemple, itération cyclique ,Planification dynamique, etc
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
Apparemment, il s'agit d'un ordre à bulles avec une complexité temporelle de O(N^2)
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n - 1;
// [begin, end]:beginEtend C'est l'intervalle de fermeture gauche - droite ,Il y a donc=No.
while (begin <= end)
{
int mid = begin + ((end - begin) >> 1);
if (a[mid] < x)
begin = mid + 1;
else if (a[mid] > x)
end = mid - 1;
else
return mid;
}
return -1;
}
Apparemment, pour les deux points ,La complexité temporelle estO(logN)
La recherche binaire est un très bon algorithme ,
Mais les inconvénients sont évidents.,
Trouver à trier en premier , Et assurez - vous que les adresses de données sont continues
Trois、Complexité spatiale
1.Définition de la complexité spatiale
La complexité spatiale est également une expression mathématique,Est une mesure de la taille de l'espace de stockage temporairement occupé par un algorithme pendant qu'il est en cours d'exécution .
La complexité spatiale n'est pas ce que le programme prendbytesDe l'espace, Parce que ça n'a pas beaucoup de sens,Donc la complexité spatiale compte le nombre de variables.
Les règles de calcul de la complexité spatiale sont essentiellement similaires à celles de la complexité pratique,Utilisez aussi BigOReprésentation progressive.
2.Caractéristiques de la complexité spatiale
Attention!:Espace de pile nécessaire à l'exécution de la fonction
(Paramètres de stockage、Variables locales、Quelques informations sur les registres, etc)Déterminé lors de la compilation,
Par conséquent, la complexité spatiale est principalement déterminée par l'espace supplémentaire explicitement appliqué par la fonction au moment de l'exécution.
3.FAQ analyse de la complexité spatiale
void BubbleSort(int* a, int n)
{
assert(a);// Le pointeur doit d'abord déclarer , Empêcher le pointeur d'être vide
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
{
break;
}
}
}
Complexité spatialeO(1) Constante
long long* Fibonacci(size_t n)
{
if (n == 0)
return NULL;
long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
}
return fibArray;
}
C'est ouvert.NEspace,Complexité temporelleO(N)
// Comment calculer la récursion factorielle FacLa complexité spatiale de?
long long Fac(size_t N)
{
if (N == 0)
return 1;
return Fac(N - 1) * N;
}
Complexité temporelleO(N),Récursivement appeléNUne fois,C'est ouvert.NCadres de pile,Chaque cadre de pile utilise un espace constant.
Note::Niveau d'auteur limité,En cas d'erreur,Veuillez corriger!!!
版权声明
本文为[Poisson de fond]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204220519179033.html
边栏推荐
- [WPF] customize combobox
- [I. XXX pest detection project] 2. Trying to improve the network structure: resnet50, Se, CBAM, feature fusion
- 【WPF】UpdateSourceTrigger
- Three locking methods of the bottom layer of synchronized: (3.21-3.27)
- Send a shutdown command to the LAN computer every 30 seconds
- MySQL數據庫第十一次作業-視圖的應用
- Pass files when openfeign is called
- scanf、printf的输入输出(格式控制符)
- 【高通SDM660平台】(8) --- Camera MetaData介绍
- Mysql database for the 11th time
猜你喜欢

【WPF】Popup

VIM is so difficult to use, why are so many people keen?

Nexus private server - (III) using private server warehouse in project practice

How to modify the IP address of the rancher server
![[WPF] customize combobox](/img/99/21298293139f6acb9d0144236b825e.png)
[WPF] customize combobox
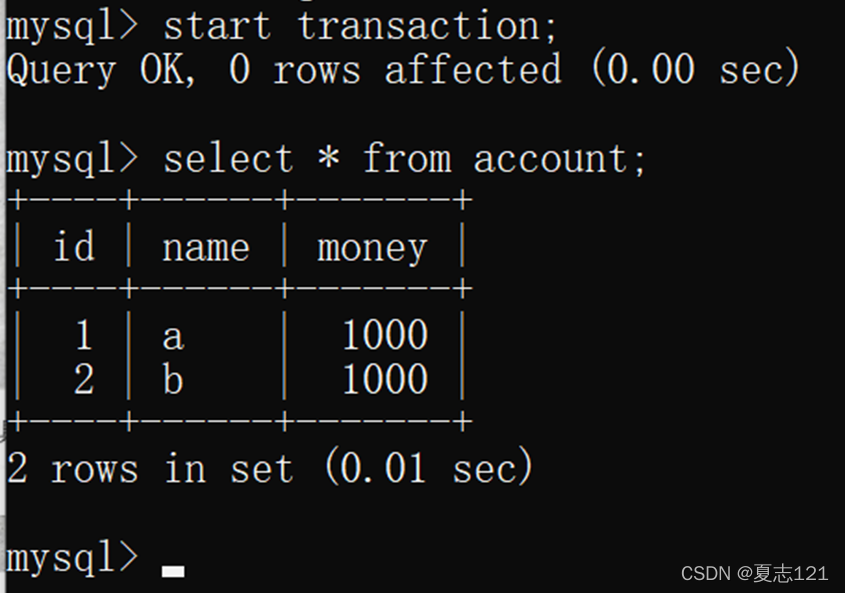
数据库第十三次作业 事务管理

Introduction to JUnit
![[WPF] cascaded combobox](/img/19/a83dc60abcfcc6ddcf06dc80860ab6.png)
[WPF] cascaded combobox

abcabc

Measuring the global recursive DNS infrastructure: a view from the edge
随机推荐
How to restrict Oracle sub query
TDD development mode and DDD development mode
Western dichotomy and Eastern trisection
数据库(二)MySQL表的增删改查(基础)
什么是幂等性
Multi level cache architecture for 100 million traffic
[I. XXX pest detection items] 3. Loss function attempt: focal loss
The problem that the video in video becomes muted when the mouse scrolls
Nexus private server - (II) console installation of version 3.2.0, initial password location
2022-1-17 to 2022-1-30 iterator mode
feign调用服务,被调用服务seata事务不开启或者xid为空
Enum enumeration type
Acrobat Pro DC tutorial: how to create PDF using text and picture files?
[WPF] custom control
PyTorch搭建双向LSTM实现时间序列预测(负荷预测)
WeChat official account looks at UIN, and it is biz after Base64.
Summary of browser cross domain problems
Empty object mode (3.14-3.20)
Nexus私服——(三) 在项目实战中使用私服仓库
Linked list (C language)