当前位置:网站首页>数学基础(二)逆矩阵、伪逆矩阵、最小二乘解、最小范数解
数学基础(二)逆矩阵、伪逆矩阵、最小二乘解、最小范数解
2022-08-08 08:00:00 【Billie使劲学】
举一个多元线性回归的例子:
假设 都为n维的行向量,N表示样本个数,y为实数。
都为n维的行向量,N表示样本个数,y为实数。

则得到到,其中, 为向量
为向量 中的n个值;
中的n个值; 就是要估计的参数。
就是要估计的参数。

将上式写成矩阵的形式就是

我们的目的就是要解出参数a的列向量,则通过下式即可解出a向量。

但是通常情况下样本量N并不等于每个样本的维度n,
则求 的最小值
的最小值 ![]()
对a求偏导,导数等于0处去最小值![]()
【置于为什么求偏导后的式子是这样的,我放到了最后说明,该结论记住即可】
移项得![]()
那么 是否可逆呢?如果可逆,就可以通过
是否可逆呢?如果可逆,就可以通过 求得a向量。
求得a向量。
下面判断 是否可逆,当
是否可逆,当 时,有两种情况,N>n 和 N<n。
时,有两种情况,N>n 和 N<n。
①N>n
其中, ,
, ,则
,则

![]() 这个就是伪逆矩阵,当X可逆时,它就是逆矩阵。
这个就是伪逆矩阵,当X可逆时,它就是逆矩阵。
伪逆矩阵对应的解法叫做最小二乘解。
②N<n
其中, ,
, ,则
,则

注意:
此时 不可逆该怎么办呢?
不可逆该怎么办呢?
我们就需要在![]() 后面加入一个正则项
后面加入一个正则项![]() 。
。
为什么要加入正则项呢?针对N<n,样本量不足,属于过拟合现象,针对过拟合问题,我们就会对代价函数加入正则项来缓解过拟合。(加入正则项求的解叫做最小范数解)
对a求偏导得到![]()
移项:
为什么 必为可逆呢?
必为可逆呢? 肯定是可逆的,故加上
肯定是可逆的,故加上 (半正定矩阵,上一章证明过)也是可逆的。
(半正定矩阵,上一章证明过)也是可逆的。
证明一下:

其中 是试探向量,故
是试探向量,故 ,所以2式为是正定的,非半正定。
,所以2式为是正定的,非半正定。
这个公式叫做岭回归![]() ,在对角线上加入了 λ,就像山岭一样。
,在对角线上加入了 λ,就像山岭一样。
对矩阵求偏导:

边栏推荐
猜你喜欢
随机推荐
分清成员函数非成员函数和友元函数
数控机床工作平台位置伺服系统的的数学建模与仿真
DBeaver 22.1.4 发布,可视化数据库管理平台
优先队列的实现原理
2022/8/7
antdv4 升级指北
攻防世界——web2
超强企业建站系统介绍:五大特点
阿里巴巴的三个“一”打通业务价值
js中call、bind、apply的区别?
用于一型糖尿病血糖调节的无模型iPID控制器
volatile在C语言中的基本使用方法
正则表达式
蓝牙5.2新特性 - Enhance ATT
动手学数理统计(1)
用平衡二叉搜索树解决硬木种类问题
JLink Commander调试方法
大文件上传时如何做到 秒传?
regular expression
数据库_JDBC

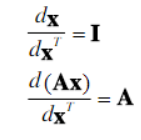
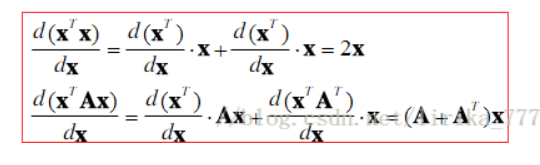
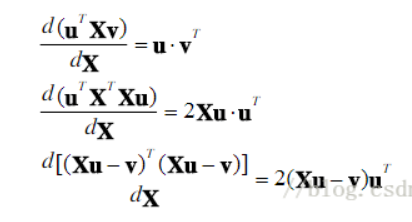


![[Optimized scheduling] Based on particle swarm to realize economic scheduling optimization of microgrid under grid-connected model with matlab code](/img/a8/ce83c9488f4fccb202482d7b7e6c05.png)