二维费用的背包问题 ← 模板题

【题目来源】
https://www.acwing.com/problem/content/description/8/

【题目描述】
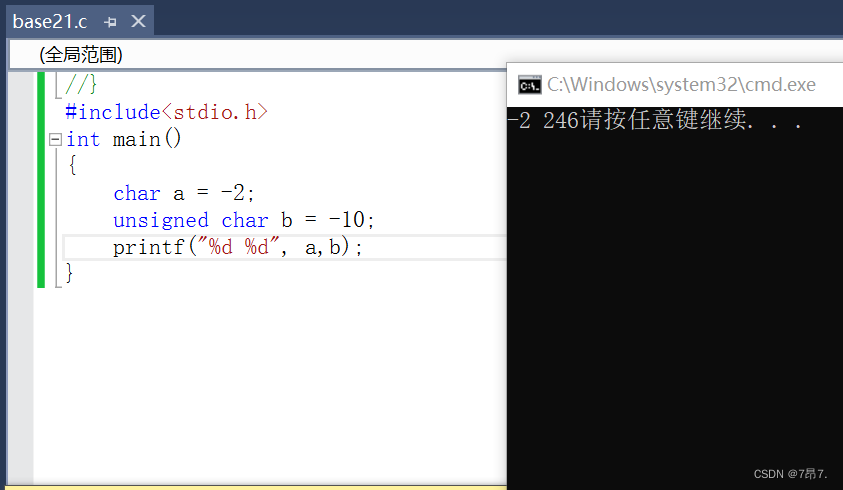
有 N 件物品和一个容量是 V 的背包，背包能承受的最大重量是 M。
每件物品只能用一次。体积是 vi，重量是 mi，价值是 wi。
求解将哪些物品装入背包，可使物品总体积不超过背包容量，总重量不超过背包可承受的最大重量，且价值总和最大。
输出最大价值。

【输入格式】
第一行三个整数，N,V,M，用空格隔开，分别表示物品件数、背包容积和背包可承受的最大重量。
接下来有 N 行，每行三个整数 vi,mi,wi，用空格隔开，分别表示第 i 件物品的体积、重量和价值。

【输出格式】
输出一个整数，表示最大价值。

【数据范围】
0<N≤1000
0<V,M≤100
0<vi,mi≤100
0<wi≤1000

【算法分析】
二维费用的背包问题，即具有两种限制条件的背包问题，它是常见背包问题的一个简单的常见扩展。也就是说，常见的背包问题都会存在二维费用的扩展。如二维费用的0-1背包问题、二维费用的完全背包问题、二维费用的多重背包问题、二维费用的分组背包问题等。

二维费用的背包问题，要求对于装入背包的每个物品 i，必须同时满足两种不同的限制条件 vol1[i] 与 vol2[i]，且每种限制条件的上限分别为 V1 与 V2。若设将物品 i 装入背包可获得的价值为 val[i]，请问怎么选择物品，可得到最大价值。

下面以二维费用的0-1背包问题为例，给出一般的二维费用背包问题的解题思路如下：
令 c[i][j][k] 表示将前 i 个物品装入限制条件1为 j、限制条件2为 k 时，可获得的最大价值。
根据求解普通0-1背包问题的状态转移方程的思路，相应可得二维费用的0-1背包问题的状态转移方程为：
c[i][j][k] = max(c[i−1][j][k], c[i−1][j−vol1[i]][k−vol2[i]] + val[i] )

类似于将普通0-1背包问题由二维优化为一维的思路（0-1背包问题的一维数组优化解析_hnjzsyjyj的博客-CSDN博客），可以将二维费用的0-1背包问题由三维优化为二维，从而达到降低算法时间复杂度的目的。优化为二维后的二维费用的0-1背包问题的状态转移方程为：
c[j][k] = max(c[j][k], c[j−vol1[i]][k−vol2[i]] + val[i])

编写代码时，一般采用如下的3重循环： 

for (i=1; i<=n; i++)   // 此行语句也常用 while(n--) 代替，其中的n为物品个数
	for (j=V1; j>=vol1[i]; j--)
		for (k=V2; k>=vol2[i]; k--) {
			c[j][k]=max(c[j][k],c[j-vol1[i]][k-vol2[i]]+val[i]);
		}

所求最大价值为c[V1][V2]。

【算法代码】

#include<bits/stdc++.h>
using namespace std;

const int maxn=1005;
int vol1[maxn],vol2[maxn],val[maxn];
int c[maxn][maxn];

int main() {
	int n,V,W;
	cin>>n>>V>>W;
	for(int i=1; i<=n; i++) {
		int vi,mi,wi;
		cin>>vi>>mi>>wi;
		vol1[i]=vi;
		vol2[i]=mi;
		val[i]=wi;
	}
	
	for(int i=1; i<=n; i++) {
		for(int j=V; j>=1; j--) {
			for(int k=W; k>=1; k--) {
				if(k>=vol2[i]&&j>=vol1[i])
					c[j][k]=max(c[j][k],c[j-vol1[i]][k-vol2[i]]+val[i]);
			}
		}
	}
	cout<<c[V][W]<<endl;
	
	return 0;
}


/*
in:
4 5 6
1 2 3
2 4 4
3 4 5
4 5 6

out:
8
*/

【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/126229598
https://blog.csdn.net/hnjzsyjyj/article/details/126228900