当前位置:网站首页>Queue topic: Implementing stacks with queues
Queue topic: Implementing stacks with queues
2022-08-09 21:35:00 【the great Czerny】
题目
标题和出处
标题:用队列实现栈
出处:225. 用队列实现栈
难度
4 级
题目描述
要求
请你仅使用两个队列实现一个后进先出的栈.The implemented stack should support all the operations of the normal stack( push \texttt{push} push、 pop \texttt{pop} pop、 top \texttt{top} top 和 empty \texttt{empty} empty).
实现 MyStack \texttt{MyStack} MyStack 类:
- void push(int x) \texttt{void push(int x)} void push(int x) 将元素 x \texttt{x} x 压入栈顶.
- int pop() \texttt{int pop()} int pop() 移除并返回栈顶元素.
- int top() \texttt{int top()} int top() 返回栈顶元素.
- boolean empty() \texttt{boolean empty()} boolean empty() 如果栈是空的,返回 true \texttt{true} true;否则,返回 false \texttt{false} false.
注意:
- 你只能使用队列的基本操作,Only add elements at the end of the queue、View and delete elements at the head of the queue、The operations of returning the number of elements and judging whether it is empty are valid.
- 你所使用的语言也许不支持队列.You can use a list or a deque to simulate a queue,As long as all operations are standard queue operations.
示例
示例 1:
输入:
["MyStack", "push", "push", "top", "pop", "empty"] \texttt{["MyStack", "push", "push", "top", "pop", "empty"]} ["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []] \texttt{[[], [1], [2], [], [], []]} [[], [1], [2], [], [], []]
输出:
[null, null, null, 2, 2, false] \texttt{[null, null, null, 2, 2, false]} [null, null, null, 2, 2, false]
解释:
MyStack myStack = new MyStack(); \texttt{MyStack myStack = new MyStack();} MyStack myStack = new MyStack();
myStack.push(1); \texttt{myStack.push(1);} myStack.push(1);
myStack.push(2); \texttt{myStack.push(2);} myStack.push(2);
myStack.top(); \texttt{myStack.top();} myStack.top(); // 返回 2 \texttt{2} 2
myStack.pop(); \texttt{myStack.pop();} myStack.pop(); // 返回 2 \texttt{2} 2
myStack.empty(); \texttt{myStack.empty();} myStack.empty(); // 返回 False \texttt{False} False
数据范围
- 1 ≤ x ≤ 9 \texttt{1} \le \texttt{x} \le \texttt{9} 1≤x≤9
- 最多调用 100 \texttt{100} 100 次 push \texttt{push} push、 pop \texttt{pop} pop、 top \texttt{top} top 和 empty \texttt{empty} empty
- 每次调用 pop \texttt{pop} pop 和 top \texttt{top} top 都是有效的
进阶
Can you implement stack using only one queue?
解法一
思路和算法
由于栈的特点是后进先出,So when using a queue to implement a stack,The order of elements within the queue needs to be maintained,Make the first element of the queue the last element to enqueue.
When implemented using two queues, queue 1 \textit{queue}_1 queue1 The role of is to store elements, queue 2 \textit{queue}_2 queue2 The role is to assist the operation.
In order to realize the function of the stack,Need to ensure that after each push operation, queue 1 \textit{queue}_1 queue1 The head element of the queue is always the newly added element.Therefore, the push operation is as follows:
Enqueue the element to be added to queue 2 \textit{queue}_2 queue2;
将 queue 1 \textit{queue}_1 queue1 的全部元素依次出队并入队到 queue 2 \textit{queue}_2 queue2;
将 queue 1 \textit{queue}_1 queue1 和 queue 2 \textit{queue}_2 queue2 互换.
完成上述操作后, queue 2 \textit{queue}_2 queue2 为空, queue 1 \textit{queue}_1 queue1 The head element of is the newly added element, queue 1 \textit{queue}_1 queue1 The rest of the elements and their order remain unchanged.Therefore, the effect of the above operation is in queue 1 \textit{queue}_1 queue1 The head of the team adds a newly added element, queue 1 \textit{queue}_1 queue1 The head and tail of the queue correspond to the top and bottom of the stack, respectively.
Because each push operation is maintained queue 1 \textit{queue}_1 queue1 the order of elements within,Therefore, the operation of popping the stack and viewing the top element of the stack can be easily implemented.The pop operation only needs to queue 1 \textit{queue}_1 queue1 The head element of the team can be removed and returned,The operation to view the top element of the stack only needs to return queue 1 \textit{queue}_1 queue1 的队首元素即可.
由于 queue 1 \textit{queue}_1 queue1 The role of is to store elements,Therefore, it is only necessary to judge whether the stack is empty or not queue 1 \textit{queue}_1 queue1 是否为空即可.
代码
class MyStack {
Queue<Integer> queue1;
Queue<Integer> queue2;
public MyStack() {
queue1 = new ArrayDeque<Integer>();
queue2 = new ArrayDeque<Integer>();
}
public void push(int x) {
queue2.offer(x);
while (!queue1.isEmpty()) {
queue2.offer(queue1.poll());
}
Queue<Integer> temp = queue1;
queue1 = queue2;
queue2 = temp;
}
public int pop() {
return queue1.poll();
}
public int top() {
return queue1.peek();
}
public boolean empty() {
return queue1.isEmpty();
}
}
复杂度分析
时间复杂度:构造方法的时间复杂度是 O ( 1 ) O(1) O(1),The time complexity of the push operation is O ( n ) O(n) O(n),出栈、The time complexity of checking the top element of the stack and judging whether the stack is empty is the same O ( 1 ) O(1) O(1),其中 n n n is the number of elements in the stack.
入栈操作需要将 queue 1 \textit{queue}_1 queue1 的 n n n 个元素出队,并将 n + 1 n + 1 n+1 elements are enqueued queue 2 \textit{queue}_2 queue2,共有 2 n + 1 2n + 1 2n+1 次操作,每次出队和入队操作的时间复杂度都是 O ( 1 ) O(1) O(1),因此The time complexity of the push operation is O ( n ) O(n) O(n).
出栈、Viewing the top element of the stack and determining whether the stack is empty are regular queue operations,时间复杂度都是 O ( 1 ) O(1) O(1).空间复杂度: O ( n ) O(n) O(n),其中 n n n is the number of elements in the stack.Elements need to be stored using a queue.
解法二
思路和算法
A stack can also be implemented using a queue.
When implemented using a queue,It is also necessary to maintain the order of elements within the queue,Make the first element of the queue the last element to enqueue,Therefore, it is necessary to ensure that after each push operation,The head element is always the newly added element.
There is a difference between a push operation implemented with one queue and a push operation implemented with two queues,Since there is only one queue,All elements need to be stored in the queue.The stack operation is as follows:
Count the number of elements in the queue size \textit{size} size;
Enqueue the element to be added;
the front of the queue size \textit{size} size elements are dequeued and enqueued in turn.
完成上述操作后,The head element is the newly added element,The remaining elements and order in the queue are unchanged.So the effect of the above operation is to add the newly added element at the head of the queue,The head and tail of the queue correspond to the top and bottom of the stack, respectively.
出栈操作、The operation of checking the top element of the stack and judging whether the stack is empty is the same as the solution one,Just perform the corresponding operation on the queue.
代码
class MyStack {
Queue<Integer> queue;
public MyStack() {
queue = new ArrayDeque<Integer>();
}
public void push(int x) {
int size = queue.size();
queue.offer(x);
for (int i = 0; i < size; i++) {
queue.offer(queue.poll());
}
}
public int pop() {
return queue.poll();
}
public int top() {
return queue.peek();
}
public boolean empty() {
return queue.isEmpty();
}
}
复杂度分析
时间复杂度:构造方法的时间复杂度是 O ( 1 ) O(1) O(1),The time complexity of the push operation is O ( n ) O(n) O(n),出栈、The time complexity of checking the top element of the stack and judging whether the stack is empty is the same O ( 1 ) O(1) O(1),其中 n n n is the number of elements in the stack.
Push operations need to be queued n n n 个元素出队,并将 n + 1 n + 1 n+1 个元素入队,共有 2 n + 1 2n + 1 2n+1 次操作,每次出队和入队操作的时间复杂度都是 O ( 1 ) O(1) O(1),因此The time complexity of the push operation is O ( n ) O(n) O(n).
出栈、Viewing the top element of the stack and determining whether the stack is empty are regular queue operations,时间复杂度都是 O ( 1 ) O(1) O(1).空间复杂度: O ( n ) O(n) O(n),其中 n n n is the number of elements in the stack.Elements need to be stored using a queue.
边栏推荐
- Fully automated machine learning modeling!The effect hangs the primary alchemist!
- IDEA tools commonly used configuration
- 论文分享:「FED BN」使用LOCAL BATCH NORMALIZATION方法解决Non-iid问题
- 环境:Flink版本:1.15.1jar包:flink-sql-connector-oracle
- 队列题目:用队列实现栈
- 基于CC2530 E18-MS1-PCB Zigbee DIY作品(二)
- Typora 结合 Picgo 自动上传图像
- [免费专栏] Android安全之Android工程模式
- 韩国严厉监管元宇宙相关企业
- 2022.08.08_每日一题
猜你喜欢

史上最全架构师知识图谱(纯干货)

基于CC2530 E18-MS1-PCB Zigbee DIY作品(三)

鹅厂机器狗花式穿越10m梅花桩:前空翻、单桩跳、起身作揖...全程不打一个趔趄...
![[免费专栏] Android安全之ZIP文件目录遍历漏洞](/img/11/c9116562b0ce57205e73fc442874d3.png)
[免费专栏] Android安全之ZIP文件目录遍历漏洞
WPF 实现带蒙版的 MessageBox 消息提示框

PHP 变量注释/**@var*/
Open Source Summer | List Details Display Based on Ruoyi Architecture
![[免费专栏] Android安全之Android奇淫run-as命令](/img/d5/771802eb57f24c1cf88657f5c5a724.png)
[免费专栏] Android安全之Android奇淫run-as命令
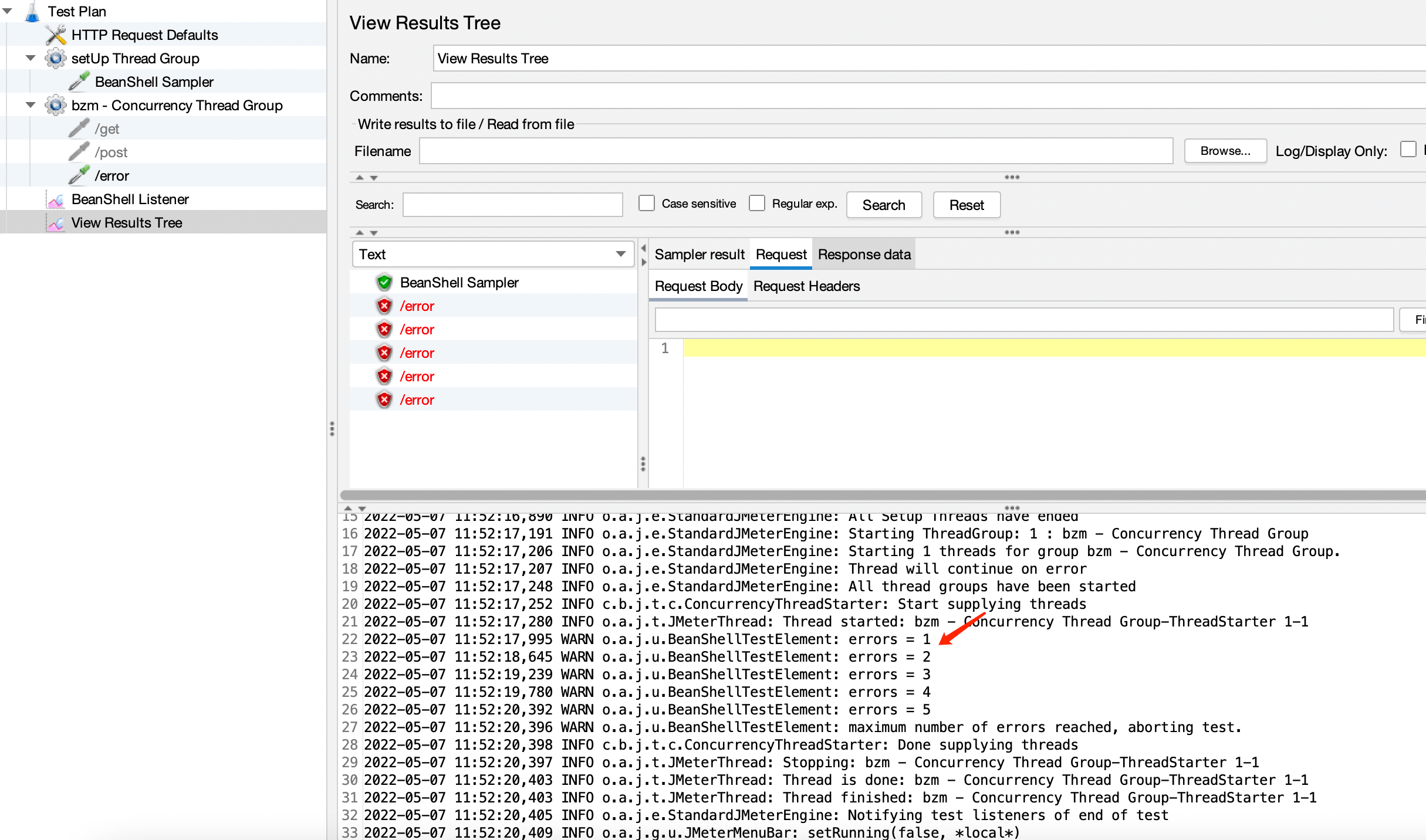
How to stop the test after reaching a given number of errors during stress testing in JMeter

Codesys结构变量编程应用(STRUCT类型)
随机推荐
宝塔面板安装使用
C#/VB.NET:从PowerPoint文档中提取文本和图片
[免费专栏] Android安全之和平精英(FZ)APK逆向分析
CreateCompatibleDC用法
字节二面:可重复读隔离级别下,这个场景会发生什么?
Openharmony轻量系统实验--GPIO点灯
基于CC2530 E18-MS1-PCB Zigbee DIY作品(二)
渗透测试——CFS三层靶机内网渗透实操
ebook下载 | 《 企业高管IT战略指南——企业为何要落地DevOps》
智驾科技完成C1轮融资,此前2轮已融4.5亿元
[免费专栏] Android安全之ZIP文件目录遍历漏洞
国内市场上的 BI 软件到底有啥区别?
对应运放 RC 滤波负反馈的波形
最新BEV感知基线 | 你确定需要激光雷达?(卡内基梅隆大学)
shell脚本编写 hash方法,shell中字符到ascii码或数字的转换
qq机器人账号不能发送群消息,被风控
基于CC2530 E18-MS1-PCB Zigbee DIY作品(三)
How to stop the test after reaching a given number of errors during stress testing in JMeter
mysql死锁的排查和解决
[免费专栏] Android安全之动态代码注入技术(利用JDB调试APK)