当前位置:网站首页>Codeforces Round #783 (Div. 2) ABCD
Codeforces Round #783 (Div. 2) ABCD
2022-04-22 05:22:00 【HeartFireY】
A.Direction Change
It can be proved that the best strategy can be transformed into taking a square diagonal matrix and then circling to the end . So it was decided 2 2 2 The situation of ( Can't turn ) Then output it .
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e5 + 100;
int ans[N];
inline void solve(){
int n, m; cin >> n >> m;
if(n > m) swap(n, m);
if(n == 1 && m > 2) cout << -1 << endl;
else{
int fir = (n - 1) + (n - 1);
int sec = (m - n) * 2;
if((m - n) % 2) sec -= 1;
cout << fir + sec << endl;
}
}
signed main(){
int t = 0; cin >> t;
while(t--) solve();
return 0;
}
B.Social Distance
There's nothing to talk about , It can be simulated directly .
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 2e5 + 100;
int a[N];
inline void solve(){
int n, m; cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> a[i];
if(m < n){
cout << "NO\n";
return;
}
sort(a + 1, a + 1 + n, [](const int x, const int y){
return x < y; });
m -= n;
for(int i = 2; i <= n; i++){
if(m < a[i]){
cout << "NO\n";
return;
}
m -= a[i];
}
if(m < a[n]) cout << "NO\n";
else cout << "YES\n";
}
signed main(){
int t = 0; cin >> t;
while(t--) solve();
return 0;
}
C.Make it Increasing
You can find , Under the optimal solution , There is and only one location is 0 0 0. Then we can directly enumerate 0 0 0 The location of , To the left... To the right . Each time, select the minimum value that meets the strict increment of the learning column as the answer .
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
inline void solve(){
int n = 0, ans = 0x3f3f3f3f3f3f3f3f; cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int pos = 1; pos <= n; pos++){
b[pos] = 0;
int nowans = 0;
for(int i = pos - 1; i; i--){
int times = (a[i] - b[i + 1]) / a[i];
nowans += times, b[i] = -a[i] * times;
}
for(int i = pos + 1; i <= n; i++){
int times = (a[i] + b[i - 1]) / a[i];
nowans += times, b[i] = a[i] * times;
}
ans = min(ans, nowans);
}
cout << ans << endl;
}
signed main(){
ios_base::sync_with_stdio(false);
//int t = 0; cin >> t;
//while(t--)
solve();
return 0;
}
D.Optimal Partition
Here you are. n n n Array of Numbers , You can divide this array into several continuous non empty sub arrays . For each array divided into, a weight can be calculated , The calculation method is as follows :
- If the sum of subarrays is 0 0 0, Then the weight of the subarray is 0 0 0
- If the sum of subarrays < 0 <0 <0, Then the weight of the subarray is − ( r − l + 1 ) -(r - l + 1) −(r−l+1)
- If the sum of subarrays > 0 >0 >0, Then the weight of the subarray is ( r − l + 1 ) (r -l + 1) (r−l+1)
Find the maximum value of the sum of the values of several continuous sub arrays .
set up d p [ i ] dp[i] dp[i] To i i i The maximum sum up to the number , Then you can write naked D P DP DP equation ( set up s [ ] s[] s[] Prefix the original array with , Pay attention to the direct elimination of + 1 +1 +1):
d p [ i ] = { d p [ j ] + ( i − j ) , s [ i ] − s [ j ] > 0 , j < i d p [ j ] , s [ i ] − s [ j ] = 0 , j < i d p [ j ] − ( i − j ) , s [ i ] − s [ j ] < 0 , j < i dp[i] = \begin{cases} dp[j] + (i - j)&, s[i] - s[j] > 0, j < i\\ dp[j]&, s[i] - s[j] = 0, j < i \\ dp[j] - (i - j)&, s[i] - s[j] < 0, j < i \end{cases} dp[i]=⎩⎪⎨⎪⎧dp[j]+(i−j)dp[j]dp[j]−(i−j),s[i]−s[j]>0,j<i,s[i]−s[j]=0,j<i,s[i]−s[j]<0,j<i
It is found that the complexity of direct computation is extremely high , So consider optimization :
- about d p [ i ] = d p [ j ] + ( i − j ) dp[i] = dp[j] + (i - j) dp[i]=dp[j]+(i−j) That is to say d p [ i ] − i = d p [ j ] − j dp[i] - i = dp[j] - j dp[i]−i=dp[j]−j
- about d p [ i ] = d p [ j ] dp[i] = dp[j] dp[i]=dp[j] unchanged
- about d p [ i ] = d p [ j ] − ( i − j ) dp[i] = dp[j] - (i - j) dp[i]=dp[j]−(i−j) That is to say d p [ i ] + i = d p [ j ] + j dp[i] + i = dp[j] + j dp[i]+i=dp[j]+j
It's not hard to find out , The process of transfer is to calculate [ 1 , s [ i ] ) [1,s[i]) [1,s[i]) in d p [ i ] dp[i] dp[i] The maximum of 、 s [ i ] s[i] s[i] It's about d p [ i ] dp[i] dp[i] Value , ( s [ i ] , n ] (s[i], n] (s[i],n] in d p [ i ] dp[i] dp[i] The maximum of .
Then you can open three segment trees , Maintain separately d p [ i ] + i , d p [ i ] , d p [ i ] − i dp[i] + i,dp[i], dp[i] - i dp[i]+i,dp[i],dp[i]−i Of m a x max max value , Every time for the position i i i Query the maximum value of three intervals ( In fact, two intervals are a single point ) Just update the answer . Note that here is s [ i ] s[i] s[i] As a subscript , Must be discretized , Otherwise, the value range is negative and the range is too large .
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 5e5 + 10, INF = 0x3f3f3f3f3f3f3f;
int a[N], s[N], f[N];
namespace SegmentTree{
#define lson rt << 1, l, mid
#define rson rt << 1 | 1, mid + 1, r
int tree[N << 2][3];
inline void push_up(int rt, int ser){
tree[rt][ser] = max(tree[rt << 1][ser], tree[rt << 1 | 1][ser]); }
void build(int rt, int l, int r){
if(l == r){
tree[rt][0] = tree[rt][1] = tree[rt][2] = -INF;
return;
}
int mid = l + r >> 1;
build(lson); build(rson);
for(int i = 0; i < 3; i++) push_up(rt, i);
}
void update(int rt, int l, int r, int ser, int pos, int val){
if(l == r && l == pos){
tree[rt][ser] = max(tree[rt][ser], val);
return;
}
int mid = l + r >> 1;
if(mid >= pos) update(lson, ser, pos, val);
else update(rson, ser, pos, val);
push_up(rt, ser);
}
int query(int rt, int l, int r, int ser, int L, int R){
if(L > R) return -INF;
if(l >= L && r <= R) return tree[rt][ser];
int mid = l + r >> 1, ans = -INF;
if(mid >= L) ans = max(ans, query(lson, ser, L, R));
if(mid < R) ans = max(ans, query(rson, ser, L, R));
return ans;
}
}
vector<int> dz;
inline int read(){
int f = 1, x = 0; char s = getchar();
while(s < '0'||s > '9'){
if(s == '-') f = -1; s = getchar(); }
while(s >= '0' && s <= '9'){
x = x * 10 + s - '0'; s = getchar();}
return x *= f;
}
inline void solve(){
int n = read();
dz.clear(); dz.emplace_back(0); f[0] = s[0] = 0;
for(int i = 1; i <= n; i++) a[i] = read(), s[i] = s[i - 1] + a[i], dz.emplace_back(s[i]), f[i] = -INF;
std::sort(dz.begin(), dz.end());
dz.erase(unique(dz.begin(), dz.end()), dz.end());
auto query_pos = [&](int x) {
return std::lower_bound(dz.begin(), dz.end(), x) - dz.begin() + 1; };
n += 1;
SegmentTree::build(1, 1, n);
for(int i = 0; i < 3; i++) SegmentTree::update(1, 1, n, i, query_pos(s[0]), 0);
#define sq SegmentTree::query
for(int i = 1; i <= n - 1; i++){
int now = query_pos(s[i]);
int a = sq(1, 1, n, 0, 1, now - 1) + i, b = sq(1, 1, n, 1, now, now), c = sq(1, 1, n, 2, now + 1, n) - i;
//cout << "i = " << i << " a = " << a << " b = " << b << " c = " << c << endl;
f[i] = max({
sq(1, 1, n, 0, 1, now - 1) + i, sq(1, 1, n, 1, now, now), sq(1, 1, n, 2, now + 1, n) - i});
SegmentTree::update(1, 1, n, 0, now, f[i] - i);
SegmentTree::update(1, 1, n, 1, now, f[i]);
SegmentTree::update(1, 1, n, 2, now, f[i] + i);
}
//for(int i = 1; i <= n - 1; i++) cout << f[i] << ' ';
cout << f[n - 1] << endl;
}
signed main(){
//ios_base::sync_with_stdio(false);
int t = 0; cin >> t;
while(t--) solve();
return 0;
}
版权声明
本文为[HeartFireY]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204220520192362.html
边栏推荐
- The chain of implicit trust: an analysis of the web third party resources loading
- 13.9.1-PointersOnC-20220421
- Typescript function generics
- Distributed transaction Seata
- 時間複雜度和空間複雜度
- Considerations for importing idea package and calling its methods
- Summary of database Deadlock: (3.7-3.13)
- Pass files when openfeign is called
- Summary of browser cross domain problems
- How to dynamically load parameters, pictures and background pictures for RDLC printing reports of ReportViewer
猜你喜欢

One way to disable Google cross domain
![[C #] remodeling matrix (staggered array)](/img/ae/7ed411e3d9bf8a9080c11a6480a7d6.png)
[C #] remodeling matrix (staggered array)
![[WPF] converter](/img/e7/c4dff7af0a9db846afd20fafb8313e.png)
[WPF] converter

Intermediary model (3.28-4.3)

【WPF】Popup
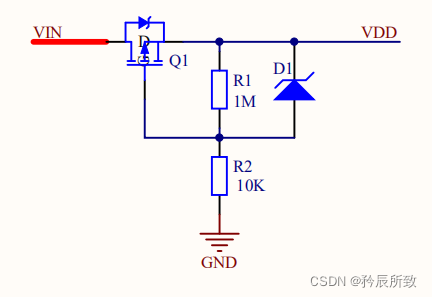
Talk about anti reverse connection circuit in combination with practice (summary of anti reverse connection circuit)
![[WPF] custom control](/img/33/c0b467805162a57966967b09eec5f0.png)
[WPF] custom control

2021-10-17

Empty object mode (3.14-3.20)

Social media and fake news in the 2016 election
随机推荐
Talk about anti reverse connection circuit in combination with practice (summary of anti reverse connection circuit)
Supporting early and scalable discovery of information websites
C LINQ's group, count, sum, write it down
What is an iterator
13.9.1-PointersOnC-20220421
After the MySQL database runs the code, the question mark is displayed in Chinese?
Temperature control via mqc582tt + PNET
[candelastudio edit CDD] - 2.3 - realize the jump between multiple securitylevels of $27 service (UDS diagnosis)
Codeforces Round #783 (Div. 2) ABCD
Enum enumeration type
String and byte [] turn to each other
Detailed explanation of ten functional features of ETL's kettle tool
Unity中的UGUI源码解析之事件系统(9)-输入模块(下)
Socket communication between server and client
Analyzing redis distributed locks from the perspective of source code
Defining "disinformation"
Neural network -- BP neural network
Measuring the impact of a successful DDoS attack on the customer behavior of managed DNS servi
2022-4-20 operation
Learning C language diary from scratch -- day27 minesweeping