1 Scalar 、 vector 、 Matrices and tensors

2 Matrix and vector multiply

3 Identity matrix and inverse matrix

3.0 Unit matrix

a = np.identity(3) #  Three row and three column identity matrix 

3.1 The matrix of the inverse

A = [[1.0,2.0],[3.0,4.0]]
A_inv = np.linalg.inv(A)
print("A  The inverse matrix ", A_inv)

3.1 Transposition

A = np.array([[1.0,2.0],[1.0,0.0],[2.0,3.0]])
A_t = A.transpose()
print("A:", A)
print("A  The transpose :", A_t)

3.2  Matrix addition

 a = np.array([[1.0,2.0],[3.0,4.0]])
b = np.array([[6.0,7.0],[8.0,9.0]])
print(" Matrix addition ： ", a + b)

3.3 Matrix multiplication

m1 = np.array([[1.0,3.0],[1.0,0.0]])
m2 = np.array([[1.0,2.0],[5.0,0.0]])
print(" According to the rules of matrix multiplication ： ", np.dot(m1, m2))
print(" Multiply by element ： ", np.multiply(m1, m2))
print(" Multiply by element ： ", m1*m2)
v1 = np.array([1.0,2.0])
v2 = np.array([4.0,5.0])
print(" Vector inner product ： ", np.dot(v1, v2))

4 Linear correlation and generating subspace

---

5 norm

5.0 Code implementation

5.0.1 Vectorial L1 L2 The infinite norm

a = np.array([1.0,3.0])
print(" vector  2  norm ", np.linalg.norm(a,ord=2))
print(" vector  1  norm ", np.linalg.norm(a,ord=1))
print(" Vector infinite norm ", np.linalg.norm(a,ord=np.inf))

5.0.2 Matrix F norm

a = np.array([[1.0,3.0],[2.0,1.0]])
print(" matrix  F  norm ", np.linalg.norm(a,ord="fro"))

5.1 The general definition of norm

A norm is a function that maps a vector to a nonnegative value . Intuitively speaking , vector x From the origin to the point x Distance of .

5.1.1 Definition

5.1 L1 norm

5.1.1 Definition

When the difference between zero and non-zero elements in machine learning is very important , In these cases , Instead, use the same slope at each position , You usually use L1 norm , It is also often used as an alternative function to represent the number of non-zero elements .

5.1.2 Mathematical expression

5.2 L2 norm / Euclid Norm

Represents starting from the origin to the vector x Euclidean distance of a certain point .

5.2.1 square L2 norm

It is also often used to measure the size of vectors , It can be calculated simply by point product , It grows very slowly near the origin .

5.2.2 square L2 Norm and L2 Norm comparison

square L2 Norm pair x The derivative of each element in depends only on the corresponding element .

L2 The derivative of the norm for each element is related to the entire vector .

5.3 Maximum norm

5.3.1 meaning

Represents the absolute value of the element with the largest amplitude in the vector ：

5.3.2 Definition

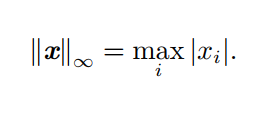
 5.4 F norm

5.4.1 meaning

F Norm is used to measure the size of the matrix

5.4.2 Mathematical definition

 5.5 Use norm to express dot product

6 Special matrix

6.1 Diagonal matrix

Contains only non-zero elements on the main diagonal , All other positions are zero .

6.1.1 The meaning of diagonal matrix

By limiting some matrices to diagonal matrices , We can get a lower computational cost （ And to the point ） Algorithm .

6.1.2 Multiplication calculation of nonstandard diagonal matrix

 6.2 Symmetric matrix

 6.3 Orthogonal matrix

Row vector and column vector are square matrices which are respectively standard orthogonal ：

 6.4 Unit vector and orthogonal

6.5 Orthonormal

If these vectors are not only orthogonal to each other , And the norm is 1, So we call them orthonormal .

7 Characteristics of decomposition

7.0 Code implementation ： Characteristics of decomposition

A = np.array([[1.0,2.0,3.0],
[4.0,5.0,6.0],
[7.0,8.0,9.0]])
#  Calculate eigenvalues 
print(" The eigenvalue :", np.linalg.eigvals(A))
#  Calculate the eigenvalues and eigenvectors 
eigvals,eigvectors = np.linalg.eig(A)
print(" The eigenvalue :", eigvals)
print(" Eigenvector :", eigvectors)

7.1 Definition

The matrix is decomposed into a set of eigenvectors and eigenvalues .

7.2 computing method

 7.3 Tip

Not every matrix can be decomposed into eigenvalues and eigenvectors .

Every real symmetric matrix can be decomposed into real eigenvector and real eigenvalue .

 7.4 Positive definite 、 Semi positive definite 、 Negative definite 、 Seminegative definite matrix

1. A matrix in which all eigenvalues are positive is called a positive definite matrix .
2. A matrix whose eigenvalues are nonnegative is called a positive semidefinite matrix .
3. A matrix in which all eigenvalues are negative is called a negative definite matrix .
4. A matrix whose eigenvalues are all non positive numbers is called a semi negative definite matrix .

8 Singular value decomposition （singular value decomposition, SVD）

8.0 The code realizes singular value decomposition

A = np.array([[1.0,2.0,3.0],
[4.0,5.0,6.0]])
U,D,V = np.linalg.svd(A)
print("U:", U)
print("D:", D)
print("V:", V)

8.1 meaning

The matrix is decomposed into singular vectors and singular values .

8.1 Decomposition calculation method

 9 Pseudo inverse

9.1 Problem solved

If matrix A The number of rows is greater than the number of columns , Then the above equation may not have a solution . If matrix A The number of rows is less than the number of columns , Then the above matrix may have multiple solutions .

9.2  The calculation process  

10 Trace operation

10.1 The definition of trace

10.2  Trace operation provides a description matrix Frobenius The way of norm ：

10.3  Operational rules

10.3.1 Trace operation is invariant under transpose operation

10.3.2  Trace of square matrix obtained by multiplication of multiple matrices , It's the same trace that multiplies the last of these matrices when they're moved to the front .

10.3.3  After cyclic permutation, the shape of the matrix obtained by the matrix product changes , The result of trace operation remains unchanged .

 10.3.4  Scalar is still itself after trace operation

 11 determinant

11.1 Definition

determinant , Write it down as det(A), It's a general square A Functions mapped to real numbers .

11.2 The characteristics of determinant

1. Determinant is equal to the product of matrix eigenvalue .
2. The absolute value of determinant can be used to measure the expansion or reduction of space after matrix multiplication .
3. If the determinant is 0, Then space shrinks completely along at least one dimension , Make it lose all its volume .
4. If the determinant is 1, So this transformation keeps the volume of space constant .