当前位置:网站首页>【控制】动力学建模简介 --> 牛顿-欧拉 (Newton-Euler) 法和拉格朗日 (Lagrange) 法
【控制】动力学建模简介 --> 牛顿-欧拉 (Newton-Euler) 法和拉格朗日 (Lagrange) 法
2022-08-08 14:23:00 【Zhao-Jichao】
1 机器人动力学建模方法
多体系统动力学形成了多种建模和分析的方法,早期的动力学研究主要包括牛顿-欧拉 (Newton-Euler) 矢量力学方法和基于拉格朗日 (Lagrange) 方程的分析力学方法。这种方法对于解决自由度较少的简单刚体系统,其方程数目比较少,计算量也比较小,比较容易。但是,对于复杂的刚体系统,随着自由度的增加,方程数目会急剧增加,计算量增大。
随着时代的发展,计算机技术得到了突飞猛进的进步,虽然可以利用计算机编程求解出动力学方程组,但是,对于求解下一时刻的关节角速度需要合适的数值积分方法,而且需要编写程序。虽然这种方法可以求解出方程的解,但是,由于这种编程方法不具有通用性,针对每个具体问题,都需要编程求解,效率比较低。因此,如果能在动力学建模的同时就考虑其计算问题,并且在建模过程中考虑其建模和求解的通用性,就能较好的解决此问题。其中,比较著名的方法有 Kane 方法、变分方法、 Roberson-Wittenburg 方法、和旋量方法等多体动力学研究方法。
1.1 牛顿-欧拉法
牛顿-欧拉方法是最开始使用的动力学建模分析方法,由于牛顿方程描述了平移刚体所受的外力、质量和质心加速度之间的关系,而欧拉方程描述了旋转刚体所受外力矩、角加速度、角速度和惯性张量之间的关系,因此可以使用牛顿-欧拉方程描述刚体的力、惯量和加速度之间的关系,建立刚体的动力学方程。
牛顿方程 (刚体平移): 外力、质量、质心加速度
欧拉方程 (刚体旋转): 力矩、角加速度、角速度、惯性张量
此方法分析了系统中每个刚体的受力情况,因此物理意义明确,表达了系统完整的受力关系。对于刚体数目较少时,计算量较小,但是随着刚体数目的增多,方程数目会增加,导致计算量较大,从而使得计算效率变低。
关于牛顿-欧拉法的总结具体如下:
- 牛顿-欧拉方程中牛顿方程主要用于解决刚体的平动问题,欧拉方程主要解决刚体的旋转问题;
- 任何刚体的任何运动均可以用平动以及转动合成,力的平移会产生转矩,力矩的平移可以直接进行;
- 刚体的受力分析可以集中到一个点;
- 多体系统的牛顿-欧拉方程建模只是动力学的建模算法之一;
- 目前建立的牛顿-欧拉方程仅仅是多刚体系统在自由运动空间的动力学方程,且可以在静力分析时候引入外部作用力和力矩;但是多刚体的接触情况需要单独进行,因为多刚体的接触是一个很复杂的情况,涉及情况较多;
- 多刚体动力学分析相对单刚体动力学需要引入多刚体的运动学分析,运动学分析需要求解刚体的线速度以及角速度,进而求解出刚体的线加速度以及角加速度
1.2 拉格朗日法
拉格朗日方程是另一种经典的动力学建模方法,牛顿-欧拉方程可以被认为是一种解决动力学问题的力平衡方法,而拉格朗日方程则是采用另外一种思路,它以系统的能量为基础建立起动力学模型。
在建模过程中不同于牛顿-欧拉方法,它可以避免内部刚体之间出现的作用力,简化了建模过程。缺点是其物理意义不明确,而且对于复杂系统,拉格朗日函数的微分运算将变得十分繁琐。
2 机器人动力学建模方法分类

机器人动力学建模方法分类

力学量和运动量之间的关系
Ref.
边栏推荐
猜你喜欢

手把手教你设计一个全局异常处理器
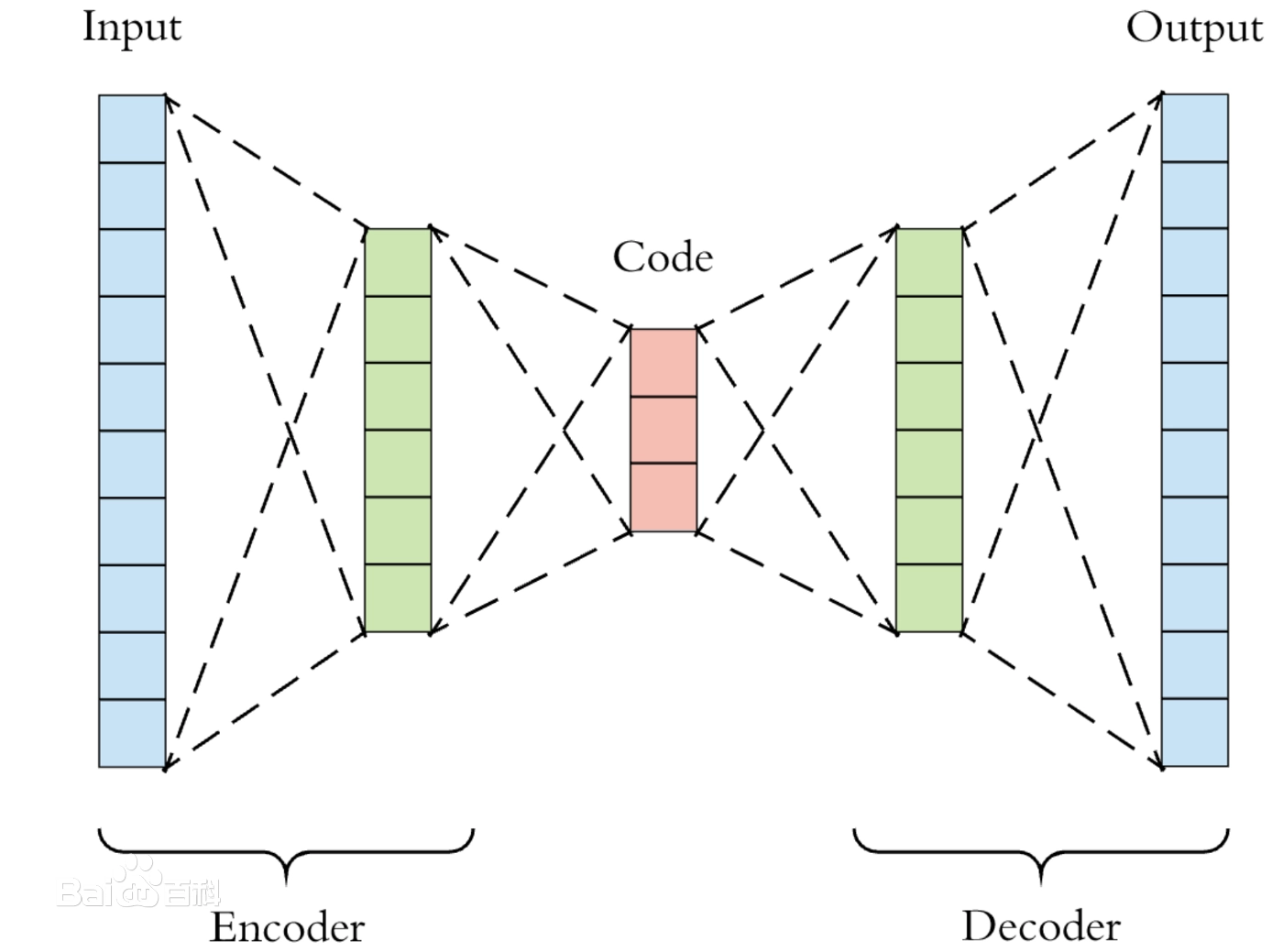
【Kaggle】Save My Paper 基于自编码器的文本图像去噪

译文推荐|深入解析 BookKeeper 协议模型与验证
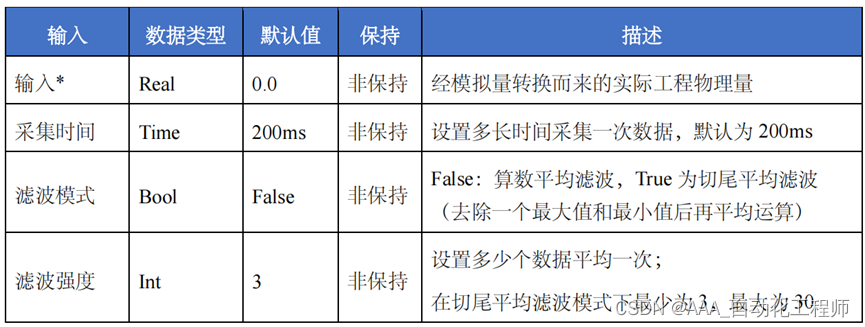
基于SCL语言的模拟量平均值滤波FB库功能介绍及创建FB库的具体方法

什么是发饰hair accessories?

idea增加左右箭头

Review: What is the pre-approval of autumn recruitment?What is an ordinary autumn move?It's all recruitment, why do you need to set these two recruitment time periods?

「复盘」面试BAMT回来整理398道高频面试题,助你拿高薪offer
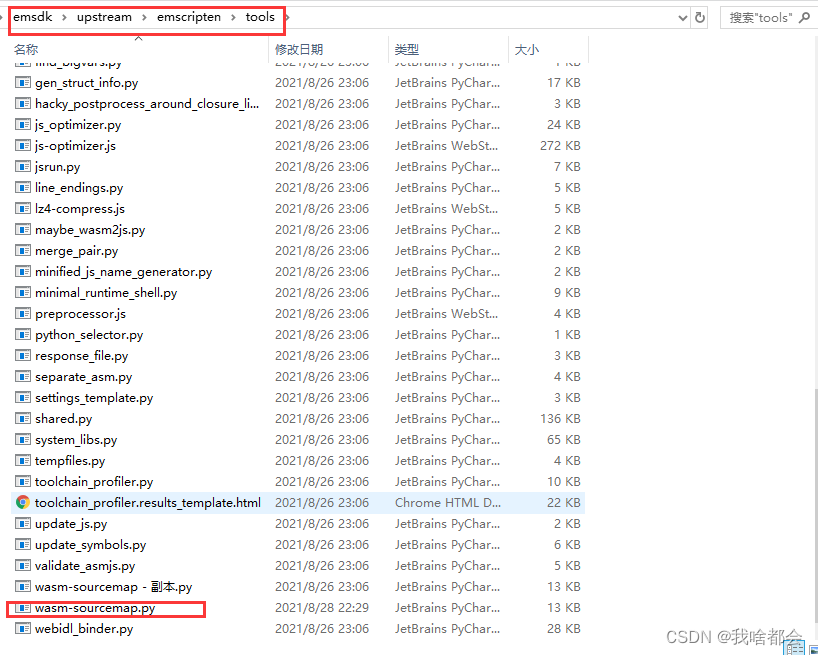
QtWebassembly遇到的一些报错问题及解决方案
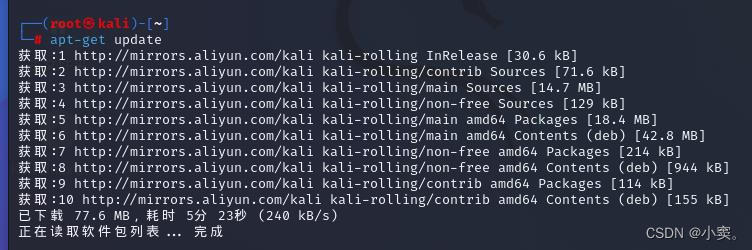
kali换源详细步骤
随机推荐
Verilog语法基础HDL Bits训练 09
OpenInfra Days China 2022 |StreamNative 翟佳、刘德志受邀分享
【Rust—LeetCode题解】1.两数之和
机器学习+深度学习笔记(持续更新~)
兔起鹘落全端涵盖,Go lang1.18入门精炼教程,由白丁入鸿儒,全平台(Sublime 4)Go lang开发环境搭建EP00
【LeetCode】761. Special binary sequence
OrderedDict构建函数模块的不常见写法
pip install xxx 出现 AttributeError: ‘tuple’ object has no attribute ‘read’ 错误
kali换源详细步骤
「PHP基础知识」检测数据类型
【系统设计】S3 对象存储
【小码匠自习室】重做ABC250-D, 我无力反抗
2022-08-07 第五小组 顾祥全 学习笔记 day31-集合-Map集合
活动报名| StreamNative 受邀参与 ITPUB 在线技术沙龙
PC端实用软件推荐
RecyclerView 实现拖拽、滑动删除
KMP Media Group South Africa implemented a DMS (Document Management System) to digitize the process, employees can again focus on their actual tasks, providing efficiency
"Small yards artisan study room" friends of friends is not a friend
WPF 常用布局方式
华为云会议的优势【华为云至简致远】