归并排序方法就是把一组n个数的序列，折半分为两个序列，然后再将这两个序列再分，一直分下去，直到分为n个长度为1的序列。然后两两按大小归并。如此反复，直到最后形成包含n个数的一个数组。

归并排序总时间=分解时间+子序列排好序时间+合并时间

无论每个序列有多少数都是折中分解，所以分解时间是个常数，可以忽略不计。

则：归并排序总时间=子序列排好序时间+合并时间

如果假设一个序列有n个数的排序时间为T(n)，T(n)是一个关于n的函数，随着n的变化而变化。

那么我们将n个数的序列，分为两个(n/2)的序列。

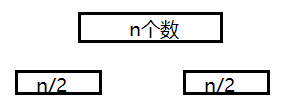
那么T(n)=2*T(n/2)+合并时间

由于合并时，两个子序列已经组内排好序了，那我们将两个排好序的序列组合成一个大的有序序列，只需要一个if循环即可。if循环中有n个数需要比较，所以时间复杂度为n。

那么T(n)=2*T(n/2)+n

我们再将两个n/2个序列再分成4个(n/4)的序列。

一个（n/2）序列排序时间=两个(n/4)的序列排序时间+两个(n/4)的序列的合并为一个（n/2）的序列时间

T(n/2)=2*T(n/4)+n/2

将T(n/2)带入到T(n)中，T(n)=2*(2*T(n/4)+n/2)+n，

通过化简T(n)=4*T(n/4)+2n

我们再将4个n/4个序列再分成8个(n/8)的序列。

T(n/4)=2*T(n/8)+n/4

将T(n/4)带入到黄色公式中，T(n)=4*(2*T(n/8)+n/4)+2n

通过化简T(n)=8*T(n/8)+3n

······

这样分下去，前面我们已经说过了，分为n个序列，每个序列里只有一个数为止。

前面我们假设的一个序列有n个数的排序时间为T(n)，现在每个序列只有一个数，所以不需要进行组内排序，时间复杂度为0。T(1)=0

大家有没有找到规律，右边式子中n前面的系数随着层数的增加而增加，第一层公式中没有n，则系数为0，第二层n的系数为1，第三层为2，第四层为3。那么规律就出来了，n前面的系数为层数减1。

那这个图有没有很熟悉，就像一个二叉树一样，通过二叉树的知识点我们可以知道，一个n个结点的完全二叉树层数为(log2n)+1。

那么n前面的系数为层数减1。

(log2n)+1-1=log2n

那log2n就是最底层n的系数。

那么我们最后一层是不是可以这样表示

T(n)=n*T(1)+(log2n)*n

T(1)=0，那么T(n)=(log2n)*n

所以归并排序的时间复杂度为nlog2n