状态压缩DP——例题 + 图，详细讲解(一)

前言：

状态压缩DP一般是基于二进制进行的，读者需要对位运算有一定的前置知识

状态压缩DP一般分为两类：

①基于连通性DP（棋盘式）

②集合式（表示每一个元素是否在集合中）

本文讲的是第一类，基于连通性DP

状压DP定义:

动态规划算法的过程是随着阶段的增长，在每个状态维度上的分界点组成了DP拓展的轮廓。对于某些问题，我们需要在动态规划的状态中记录一个集合，保存这个轮廓的详细信息，以便于进行状态转移。若集合大小不超过 N ，集合中每个元素都是小于 k 的自然数，则我们可以把这个集合看做一个 N  位 k 进制数，以一个 [0,k^N-1] 之间的十进制整数的形式作为DP状态的一维。这种把集合转化为整数记录在DP状态中的一类算法被称之为状态压缩动态规划算法。
 

我们先用一个例子来说明状态压缩DP的一般解法：

例一: 小国王

在n×n 的棋盘上放 k 个国王，国王可攻击相邻的 8 个格子，求使它们无法互相攻击的方案总数。

输入格式

共一行，包含两个整数 n 和 k。

输出格式

共一行，表示方案总数，若不能够放置则输出00。

数据范围

1≤n≤10,
0≤k≤n^2

输入样例：

3 2

输出样例：

16

国王攻击范围示意图

红色表示国王位置，蓝色表示攻击范围

 算法分析：

类似于棋盘放置类问题， 在一般情况下我们会采用暴搜（如八皇后问题）,但如果我们直接暴搜，时间复杂度为O（）,明摆着会超时的，因此可以考虑用记忆化搜索来优化。

于是我们用动态规划来考虑这个问题：
动态规划的转移方程，一般由最后一个不同点来定，由国王攻击方式我们可以发现，

第i层放置国王的行为受到第i - 1层和第 i + 1 层以及第 i 层国王影响。

那么我们可以按照一般套路，从上往下枚举每一行，这样考虑第 i 层状态时，只需考虑 i−1 层的状态即可。

于是，我们可以考虑把层数 i 作为动态规划的 一个阶段 进行 线性DP，

根据一般的DP思考方式，我们记录第i阶段所需要的信息

第 i 阶段需要记录的就是前 i 层放置的国王数量 j，以及在第 i 层的 棋盘状态 s

这里，我们先分析一下，哪些棋盘状态是合法的， 以及哪些棋盘转移的状态是合法的（注意这两个状态，后面代码实现时会用到）

合法的棋盘状态：

如上图所示，蓝色方块为摆放国王的位置，红色方块为国王的 攻击范围

只要任意王之间只要不相邻，那么就是合法的状态

棋盘转移的合法状态：

如上图所示：

 只要任意国王的 纵坐标不相邻，就是 合法的转移状态。

那么怎么用代码实现表示这些状态呢？

我们可以用二进制来表示这些状态

 我们给它标上号，让有国王的位置设为1，没国王的位置设为0，于是可以得到(0100010)

于是，我们可以用(state >> i ) == 1, 来判断在当前状态s下的第i个位置(0 <= i < n)是否放了国王。

同时，因为枚举i-1层的状态和第i层的状态所需的循环过多导致时间复杂度很高,所以在这里我们运用预处理的方式来解决此题

状态表示：f[ i ][ j ][ s ]所有只摆了前i行，已经摆了j个国王并且第i行摆放状态是s的所有方案集合

状态转移方程：f[ i ][ j ][ state[a] ] += f[ i - 1 ][ j - c ][ state[b] ]  (c是在选择状态a时，放置的国王数量)

状态分析图：(我们把第i行国王的放置方式，作为集合)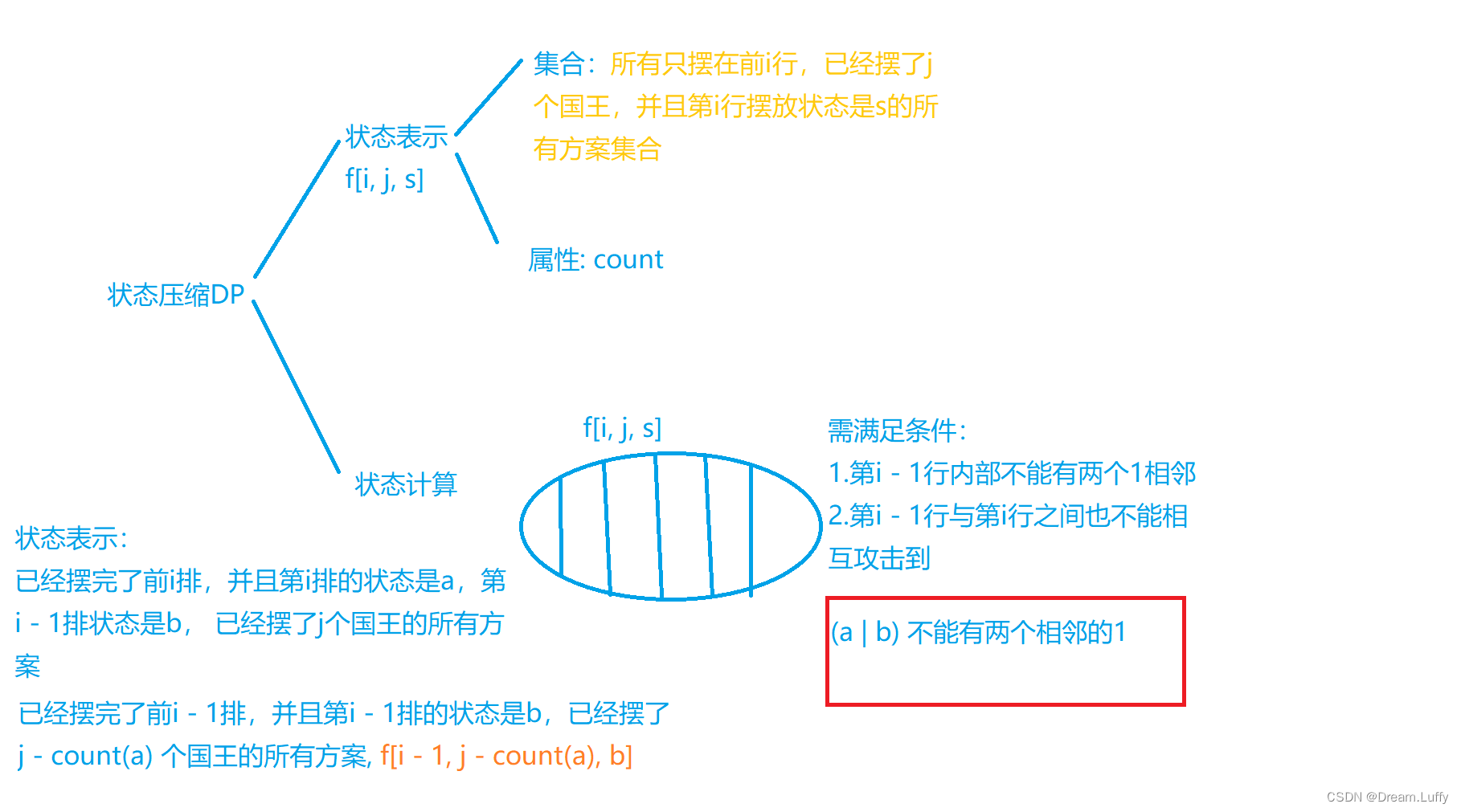

经过前面的分析，我们就可以上代码了

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>

using namespace std;
typedef long long LL;

const int N = 12, M = 1 << 10,  K = 110;

int n, m;
vector<int> state;
int cnt[M]; //状态state[a]的国王个数
vector<int> head[M];//head[i] 里存储在第i行状态为state[a]的情况下，上一行状态可以取到的合法状态statep[b]
LL f[N][K][M]; //状态转移方程，存方案数

bool check(int state)
{
    for(int i = 0;i < n;i ++) //同一行两个国王不能相邻
        if((state >> i & 1) && (state >> i + 1 & 1))
            return false;
    return true;
}

int count(int state) //统计该状态下国王，即1的个数
{
    int res = 0;
    for(int i = 0;i < n;i ++) res += state >> i & 1;
    return res;
}

int main()
{
    cin >>n >> m;
    //预处理所有合法状态 (对于这两个状态压缩有疑惑的，看看上面的图)
    for(int i = 0;i < 1 << n;i ++)
        if(check(i))
        {
            state.push_back(i); //将合法方案存入state
            cnt[i] = count(i);
        }
        //预处理所有合法状态的合法转移
    for(int i = 0;i < state.size();i ++)
        for(int j = 0;j < state.size();j ++)
        {
            int a = state[i], b = state[j];
            if((a & b) == 0 && check(a | b)) //a & b 指第i行和i-1行不能在同列有国王， check(a|b) == 1 指i和i -1行不能相互攻击到
                head[i].push_back(j);  //head[i] 里存储在第i行状态为state[a]的情况下，上一行状态可以取到的合法状态statep[b]
        }
    f[0][0][0] = 1; //求方案数时，初始方案需要为1, 在我的《背包问题》中有讲
    for(int i = 1;i <= n + 1;i ++) //枚举每一行
        for(int j = 0;j <= m;j ++) //国王数量
            for(int a = 0;a < state.size();a ++) //枚举合法方案
                for(int b : head[a])
                {
                    int c = cnt[state[a]];  //状态state[a]的国王个数
                    if(j >= c)
                        f[i][j][state[a]] += f[i - 1][j - c][state[b]]; //f[i][state[a]], 在第i行状态为i时，所有i - 1行的状态数量
                    //因为state[a]和a呈映射关系，所也可以写成
                    //  f[i][j][a] += f[i - 1][j - c][b];
                }
        cout << f[n + 1][m][0] << endl;//我们假设摆到n + 1行，并且另这一行状态为0,那么即得到我们想要的答案， 
    //如果我们用f[n][m][]来获取答案，那么我们就要枚举最后一行的所有状态取最大值，来得到答案。

通常，在内存限制较紧时，我们可以利用滚动数组来优化

由于第 i 阶段状态只会用到第 i−1 阶段的状态，因此我们可以采用滚动数组来优化空间

具体的内容，在这篇文章中有讲动态规划之背包问题_Dream.Luffy的博客-CSDN博客

//滚动数组优化
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>

using namespace std;
typedef long long LL;

const int N = 12, M = 1 << 10,  K = 110;

int n, m;
vector<int> state;
int cnt[M];
vector<int> head[M];
LL f[2][K][M];

bool check(int state)
{
    for(int i = 0;i < n;i ++) //同一行两个国王不能相邻
        if((state >> i & 1) && (state >> i + 1 & 1))
            return false;
    return true;
}

int count(int state) //统计该状态下国王，即1的个数
{
    int res = 0;
    for(int i = 0;i < n;i ++) res += state >> i & 1;
    return res;
}

int main()
{
    cin >>n >> m;
    for(int i = 0;i < 1 << n;i ++)
        if(check(i))
        {
            state.push_back(i); //将合法方案存入state
            cnt[i] = count(i);
        }
    for(int i = 0;i < state.size();i ++)
        for(int j = 0;j < state.size();j ++)
        {
            int a = state[i], b = state[j];
            if((a & b) == 0 && check(a | b)) //上下排兼容的情况
                head[i].push_back(j);
        }
    f[0][0][0] = 1; 
    for(int i = 1;i <= n + 1;i ++) //枚举每一行
        for(int j = 0;j <= m;j ++) //国王数量
            for(int a = 0;a < state.size();a ++) //枚举合法方案
            {
                f[i & 1][j][state[a]] = 0;//要先清空,因为第一维一直在循环,转移用的 += ，不清空会用到前前阶段的状态
                for(int b : head[a])
                {
                    int c = cnt[state[a]];
                    if(j >= c)
                        f[i & 1][j][state[a]] += f[i - 1 & 1][j - c][state[b]];
                    //因为state[a]和a呈映射关系，所也可以写成
                    //  f[i][j][a] += f[i - 1][j - c][b];
                }
            }
        cout << f[n + 1 & 1][m][0] << endl;

    return 0;            
}

该系列会持续更新, 我是Luffy，期待与你再次相遇