一、概述

        矩阵可以看作是空间的线性变换。矩阵A的行列式是一个数字，对应于使用该矩阵变换空间时获得的乘法变化。负行列式意味着方向发生了变化（而不仅仅是重新缩放和/或旋转）。方向的变化意味着例如在2D平面中，进行镜像。

        这是一个区分正行列式和负行列式的示例：

        可以看到，通过旋转和缩放无法获得负行列式对应的变换。

        此外，行列式还为您提供了转换量。 如果你取n维单位立方体并在其上应用矩阵A，则行列式的绝对值对应于变换后图形的面积。

二、例1

        为了计算形状的面积，我们将使用二维的简单正方形。 单位平方面积可以用勾股定理取两个单位向量来计算。

         i 和 j 的长度为 1，因此单位正方形的面积为 1。

        首先，让我们创建一个函数 plotVectors() 来绘制向量：

def plotVectors(vecs, cols, alpha=1):
    plt.figure()
    plt.axvline(x=0, color='#A9A9A9', zorder=0)
    plt.axhline(y=0, color='#A9A9A9', zorder=0)

    for i in range(len(vecs)):
        x = np.concatenate([[0,0],vecs[i]])
        plt.quiver([x[0]],
                   [x[1]],
                   [x[2]],
                   [x[3]],
                   angles='xy', scale_units='xy', scale=1, color=cols[i],
                   alpha=alpha)

        让我们从在 Python 中创建向量：

orange = '#FF9A13'
blue = '#1190FF'

i = [0, 1]
j = [1, 0]

plotVectors([i, j], [[blue], [orange]])
plt.xlim(-0.5, 3)
plt.ylim(-0.5, 3)
plt.show()

         我们应用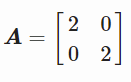给 i 和 j。 这个是个对角矩阵。 所以它会重新调整我们的空间，但是不会进行旋转。更准确地说，它将以相同的方式重新调整每个维度，因为对角线值是相同的。 让我们创建矩阵 A：

A = np.array([[2, 0], [0, 2]])

new_i = A.dot(i)
new_j = A.dot(j)
plotVectors([new_i, new_j], [['#1190FF'], ['#FF9A13']])
plt.xlim(-0.5, 3)
plt.ylim(-0.5, 3)
plt.show()

         正如预期的那样，我们可以看到 i 和 j 对应的正方形没有旋转，但 i 和 j 的长度增加了一倍。

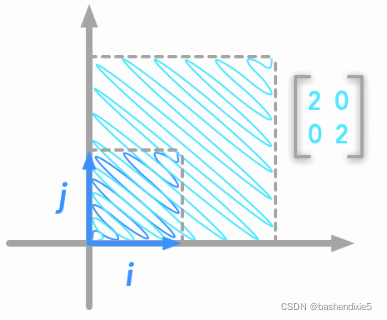
         我们现在将计算 A 的行列式（这里不讲述有关行列式计算的详细信息）：

np.linalg.det(A)
#结果为4

        可以看到，变换将单位正方形的面积乘以 4。新的i和新的j的长度为 2（因此 2⋅2=4）。

三、例2

        现在让我们看一个负行列式的例子。

        我们将用矩阵变换单位平方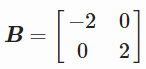：，它的行列式是 -4：

B = np.array([[-2, 0], [0, 2]])
np.linalg.det(B)
#结果为-4

         绘制

new_i_1 = B.dot(i)
new_j_1 = B.dot(j)
plotVectors([new_i_1, new_j_1], [['#1190FF'], ['#FF9A13']])
plt.xlim(-3, 0.5)
plt.ylim(-0.5, 3)
plt.show()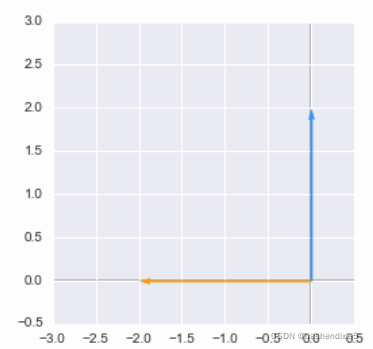

         我们可以看到，行列式为 2 和 -2 的矩阵以相同的方式修改了单位正方形的面积。

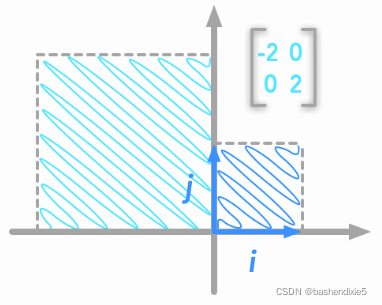
         行列式的绝对值表明，和第一个例子一样，新正方形的面积是单位正方形面积的 4 倍。 但这一次，不仅是大小变化，而且是镜像转换。

        仅使用单位向量并不明显，所以让我们使用一些随机点。         

        我们将使用矩阵

points = np.array([[1, 3], [2, 2], [3, 1], [4, 7], [5, 4]])

C = np.array([[-1, 0], [0, 1]])
np.linalg.det(C)

         由于行列式是-1，所以空间的面积不会改变。 但是，由于它是负数，我们得到无法通过旋转获得的变换：

newPoints = points.dot(C)

plt.figure()
plt.plot(points[:, 0], points[:, 1])
plt.plot(newPoints[:, 0], newPoints[:, 1])
plt.show()

         我们已经看到，矩阵的行列式是一个特殊的值，它表示了关于这个矩阵对应的变换的性质。