当前位置:网站首页>基于Qiskit——《量子计算编程实战》读书笔记(三)
基于Qiskit——《量子计算编程实战》读书笔记(三)
2022-08-10 05:29:00 【溴锑锑跃迁】

目录
第4章 使用量子门演化量子态
门
本章代码:https://github.com/PacktPublishing/Mastering-Quantum-Computing-with-IBM-QX/tree/master/Chapter04
此所谓“门”者,并非 door,而是 gate.一如量子比特是经典比特的量子版本,量子寄存器是经典寄存器的量子版本一样,量子门是经典逻辑门的量子版本。沿循我们在第三章的经典与量子间的类比思路,本章中也会以同样方式处理经典门和量子门。
在经典计算中,经典门在经典寄存器上运行以演化(Evolve)其状态,在量子计算中,量子门在量子寄存器上运行以演化量子状态。
对于 经典逻辑门,百度百科给出如下信息:

MC玩家可能对此更为熟悉,在游戏社区中被广泛应用于所谓的“红石电路”,将红石的亮与灭对应于1和0:
【MC-红石】06 【不可能学不会】萌新红石入门首选必修课(七大逻辑门)
前文已经说过,每一个量子态都可以有一个矢量去对应,更何况我们既已定义 .故而很自然地可以想到,既然我们有向量来对应单量子态,那么象征着“变换”或“演化”的量子门,就可以对应于矩阵。但是,和第三章的推导一样,我们选取的数学工具必须保证变换结果也是一个量子态,意味着分量平方和仍应是1。为了进一步推导,我们需要联系Bloch球面,既然量子态都可以被描述成端点位于球面上的矢量,那么量子态间的变换也就可以被描述成幺正矩阵。在群论中,该类矩阵被归为SU(3),其中S意味着变换前后,矢量模长不会改变,数学上表现为其行列式为1。
.故而很自然地可以想到,既然我们有向量来对应单量子态,那么象征着“变换”或“演化”的量子门,就可以对应于矩阵。但是,和第三章的推导一样,我们选取的数学工具必须保证变换结果也是一个量子态,意味着分量平方和仍应是1。为了进一步推导,我们需要联系Bloch球面,既然量子态都可以被描述成端点位于球面上的矢量,那么量子态间的变换也就可以被描述成幺正矩阵。在群论中,该类矩阵被归为SU(3),其中S意味着变换前后,矢量模长不会改变,数学上表现为其行列式为1。
拓展知识:SU(2),SO(3)群笔记 - luyi07 - 博客园 (cnblogs.com)
在二维平面中,很典型的例子是旋转矩阵:
![\\Rot(\theta)=\left[\begin{matrix} cos(\theta)&sin(\theta)\\-sin(\theta)&cos(\theta)\end{matrix} \right ]\\ det(Rot(\theta))=cos^2(\theta)-(-sin(\theta))(sin(\theta))=1](http://img.inotgo.com/imagesLocal/202208/10/202208100528215323_11.gif)
例如对零态:

这种变换令人大为满意!所以我们大可以说,旋转群对于不同的角度可以代表一系列量子门。
正式介绍全部量子门前,我们还需要注意几点(其实都是线性代数中的规定):
- 一系列门的作用顺序不能轻易改变,即交换律不一定成立,但是结合律却可以成立(联系矩阵的变换意义,尝试举出交换律不成立的例子);
- 左矢是右矢的转置加共轭,故而在左边作用于右矢的量子门绝对不能在左边作用左矢,也就是说
 没有意义!
没有意义!
另,需知,上例中的量子门为单量子门,量子门之间也可以通过直积进行组合成为多量子门,当然相应作用的量子态也必须是多量子态。
IBM QX通用门集
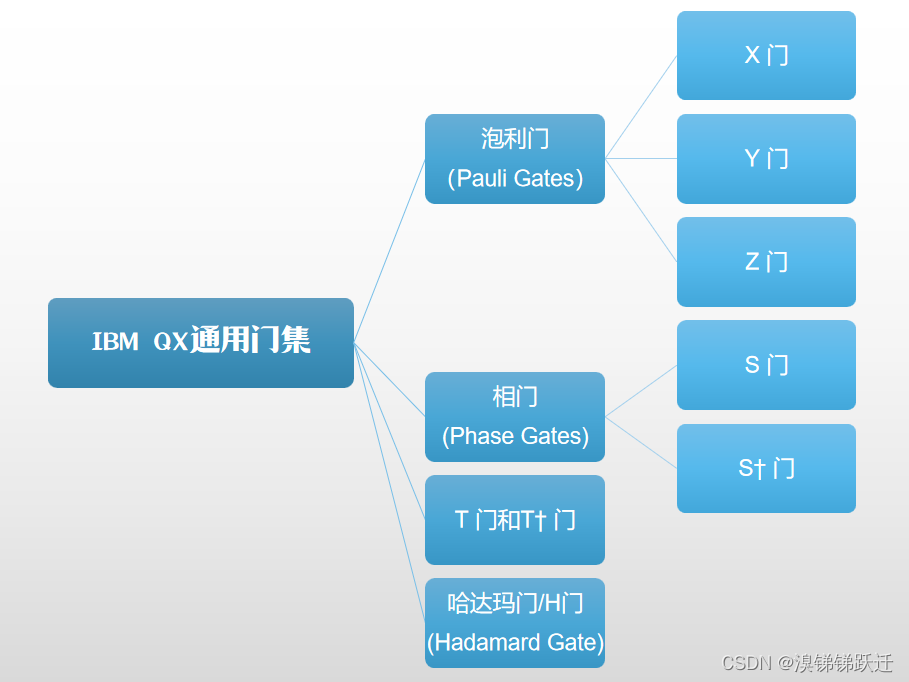
接下来的介绍会十分单调乏味,希望读者诸君可以一边浏览代码定义,一边将其作用于不同量子态上,并用我们在第二章实现的绘图工具做出相应的布洛赫球面。
哈达玛门
数学定义:![H=\frac{1}{\sqrt2}\left[\begin{matrix}1&1\\1&-1\end{matrix}\right]](http://img.inotgo.com/imagesLocal/202208/10/202208100528215323_6.gif) ;
;
几何意义:将初始量子比特绕x轴旋转180°,然后绕y轴旋转90°;
代码实现:
H=1./np.sqrt(2)*np.matrix('1 1;1 -1')泡利门(X, Y, Z)
数学定义:

几何意义:
- X门:将量子态绕X轴旋转180°;
- Y门:将量子态绕Y轴旋转180°;
- Z门:将量子态绕Z轴旋转180°;
代码实现:
X=np.matrix('0 1; 1 0')
Y=np.matrix([[0, -1j],[1j, 0]])
Z=np.matrix([[1,0],[0,-1]])相门(S)和π/8门(T)
几何意义:
- S门:将量子态绕z轴旋转90°;
- T门:将量子态绕z轴旋转45°(至于为什么是π/4弧度而不是π/8弧度,这和历史原因有关);
代码实现:
S=np.matrix([[1,0],[0,np.e**(j*np.pi/2.)]])
T=np.matrix([[1,0],[0, np.e**(j*np.pi/4.)]])其dagger门或称匕首门,亦即其共轭加转置:
S_dagger = S.conjugate().transpose()
T_dagger = T.conjugate().transpose()相应的几何意义和原先量子门大体一致:旋转角度相同,只是方向不一样。
运行以下代码,体会各量子门几何意义:
plot_bloch(H*zero_qubit)
plot_bloch(H*one_qubit)
plot_bloch(X*zero_qubit)
plot_bloch(X*one_qubit)
plot_bloch(Y*zero_qubit)
plot_bloch(Y*one_qubit)
plot_bloch(Z*zero_qubit)
plot_bloch(Z*one_qubit)
plot_bloch(zero_qubit)
plot_bloch(S*zero_qubit)
plot_bloch(T*zero_qubit)
plot_bloch(T*T*zero_qubit)多量子比特门
本节重点介绍一种极其重要的多量子比特门:CNOT,其重要性就在于其能生成纠缠态。
| 起始状态 | CNOT 门操作后状态 |
|---|---|
| | 00 > | | 00 > |
| | 01 > | | 01 > |
| | 10 > | | 11 > |
| | 11 > | | 10 > |
稍加观察与思考,不难发现,第二个比特位的量子态变化与否实际上取决于第一个量子态是1还是0.所以,我们叫第一个量子比特为控制位(control, 但实质上是作用的条件),第二个量子比特为目标位(target,但实质上是作用的结果)。
那么好,现在让我们考虑一个正零双量子态:

现在将CNOT门作用于其上:

思考:为什么得到这样一个结果?
数学定义:
![CNOT=\left[ \begin{matrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&0&1\\ 0&0&1&0 \end{matrix} \right]](http://img.inotgo.com/imagesLocal/202208/10/202208100528215323_12.gif)
代码实现:
CNOT=np.matrix('1 0 0 0; 0 1 0 0; 0 0 0 1; 0 0 1 0')由于我们目前处理的是双量子态,继续用布洛赫球绘图不免有些不合适,故而需要一个新函数来检验我们的算法:
def measure_in_01_basis(state):
from random import random
n_qubits=int(log(state.shape[0],2))
probabilities=[(coeff*coeff.conjugate()).real for coeff in state.flat]
rand=random()
for idx,state_desc in enumerate([''.join(map(str,state_desc))
for state_desc in itertools.product([0, 1], repeat=n_qubits)]):
if rand < sum(probabilities[0:(idx+1)]):
return '|"%s">' % state_desc
def probability_table_in_01_basis(state,n_measurements=1000):
from collections import Counter
measured=[measure_in_01_basis(final_state) for i in range(n_measurements)]
for s,c in Counter(measured).items():
print(s,"{0:.0%}".format(c/n_measurements))
starting_state=create_quantum_state([plus_qubit,zero_qubit])
final_state=CNOT*starting_state
probability_table_in_01_basis(final_state)注意,代码逻辑中有一处是违背量子计算原则的,即重复测量了同一个量子态并假定它不会坍缩到某一经典状态。在实际操作中,我们需要提前制备大量相同量子态,并对其中每一个态进行逐个测量,最后得到结果。
原书上附加了额外的一个例子,即以第一个量子比特为目标位,第二个量子比特为控制位:
CNOT_control1_target0=np.kron(H,H)*CNOT*np.kron(H,H) 除了思考这个例子,我还希望你能思考一下,对于n元多量子态,怎样才能任意指定控制位和目标位呢? 进一步,相应量子门的矩阵如何写出?(提示,运用行或列对调的思想)
练习和问题

欢迎加入Qiskit交流群: 1064371332
边栏推荐
- 线性代数(四)
- 接口文档进化图鉴,有些古早接口文档工具,你可能都没用过
- 暑期学前作业
- Matlab simulation of multi-factor house price prediction based on BP neural network
- 栈与队列 | 用栈实现队列 | 用队列实现栈 | 基础理论与代码原理
- 【Pei Shu Theorem】CF1055C Lucky Days
- Thread.sleep, Thread.yield role explanation
- 【LeetCode】41. The first missing positive number
- Depth of carding: prevent model fitting method
- 通过一个案例轻松入门OAuth协议
猜你喜欢
随机推荐
线性模型中的高级特征选择技术——基于R
Thread.sleep, Thread.yield 作用解释
应用在智能触摸遥控器中的触摸芯片
CORS跨域资源共享漏洞的原理与挖掘方法
众昂矿业:萤石下游需求强劲
openGauss源码,在window系统用VSCode维护吗?
【裴蜀定理】CF1055C Lucky Days
一篇文章带你搞懂什么是幂等性问题?如何解决幂等性问题?
SQLSERVER 2008 parses data in Json format
Important transformation and upgrading
【LeetCode】41. The first missing positive number
Jenkins 如何玩转接口自动化测试?
Mysql CDC (2.1.1) inital snapshot database set up five concurrent degree, se
西门子Step7和TIA软件“交叉引用”的使用
【Pei Shu Theorem】CF1055C Lucky Days
暑期学前作业
Arduino框架下合宙ESP32C3 +1.8“tft 网络时钟
FPGA engineer interview questions collection 41~50
接口调试还能这么玩?
咨询cdc 2.0 for mysql不执行flush with read lock.怎么保证bin
 没有意义!
没有意义!