[损失函数]——均方差

1. 均方差损失函数(Mean Squared Error, MSE)

均方差损失函数是预测数据和原始数据对应点误差的平方和的均值，公式为：
$$MSE=\frac{1}{N}(\hat{y}-y{)}^2$$
N为样本个数。

2. 均方差在pytorch中的用法

均方差损失函数在pytorch中的函数为：

torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')

pytorch中默认损失计算的是均值。
我看很多博客对该损失函数讲解的不是很全面，它们只告诉你这个接口怎么用而不讲解其中是怎么进行运算的，下面我用一个实例来讲解一下函数内部是如何运算的。

>>> input = torch.randn(3,5,requires_grad=True)
>>> input
tensor([[ 0.0107,  0.0574,  0.2145, -0.6022, -0.2549],
        [-0.5236, -0.0693,  0.4386,  0.1597,  2.2749],
        [-1.7281, -0.6220,  2.5002, -0.5681, -0.5767]], requires_grad=True)
>>> target = torch.randn(3,5)
>>> target
tensor([[ 0.3699, -0.7985,  1.2310,  0.3084,  2.2067],
        [ 0.2520, -1.0720,  0.1930, -0.2715,  0.7808],
        [-0.9800, -1.0310, -1.2699, -0.9418, -1.2091]])
>>> loss = nn.MSELoss()
>>> output = loss(input, target)
>>> output.backward()
>>> output
tensor(1.8899, grad_fn=<MseLossBackward>)

计算得到input和target的均方差为2.3449。下面我们不借助torch.nn.MESLoss()来计算下它们的均方差。

首先根据公式我们要计算input和target的差的平方：

>>> result = (input-output)**2
>>> result
tensor([[ 0.1290,  0.7326,  1.0333,  0.8291,  6.0594],
        [ 0.6015,  1.0054,  0.0603,  0.1860,  2.2324],
        [ 0.5596,  0.1673, 14.2134,  0.1397,  0.3998]], grad_fn=<PowBackward0>)

接着我们求result所有元素的和，然后再除以元素总个数15：

>>> result = result.view(15,).sum()/15
>>> result
tensor(1.8899, grad_fn=<DivBackward0>)

和nn.MSELoss()计算结果相同。
值得注意的是，若多分类任务中要使用均方差作为损失函数，需要将标签转换成one-hot形式，这与交叉熵损失函数恰巧相反。关于交叉熵如何使用可以参考我的另一篇博客：[损失函数]——交叉熵。
因为在使用nn.CrossEntropyLoss()时是取出激活层输出中每个样本（ 每一行）中最大的数参与损失函数的运算，而均方差则不然，它是对每一个输出都要参与运算，所以在使用均方差作为损失函数的时候要将标签转换成one-hot形式。

3. 均方差不宜和sigmoid函数一起使用

下面用公式来进行说明：
sigmoid的函数如下：
$$S(x)=\frac{1}{1+e^{-x}}$$
均方差损失函数：
$$Loss=\frac{1}{N}(\hat{y}-y{)}^2=\frac{1}{N}(S(\omega \ast x+b)-y{)}^2$$
对权值求导$\omega$：
$$\frac{\partial Loss}{\partial \omega }=\frac{2}{N}(S(\omega \ast x+b)-y)S^{\prime }(\omega \ast x+b)$$
最终变换成对sigmoid函数求导，sigmoid函数有一个特点，那就是横坐标越远离坐标原点，导数越接近于0，当$S(\omega \ast x+b)$越接近1时导数越小，最终会造成梯度消失。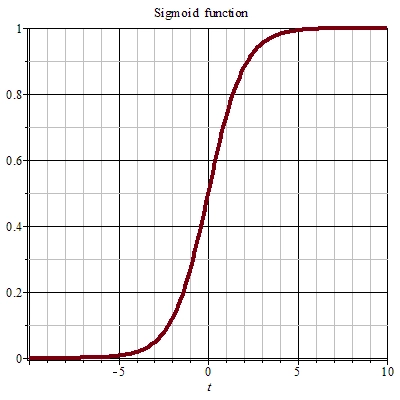

pytorch官方文档
交叉熵损失函数(Cross Entropy Error Function)与均方差损失函数(Mean Squared Error)