当前位置:网站首页>Codeforces Round #783 (Div. 2) D题解
Codeforces Round #783 (Div. 2) D题解
2022-04-23 19:12:00 【ZZXzzx0_0】
D. Optimal Partition
题意:
给你 n n n个数的数组,你可以把这个数组分为若干个连续的子数组,不能为空。
假设 s [ i ] s[i] s[i]为 a a a数组的前缀和数组
那么连续子数组 a l a_l al a l + 1 a_{l+1} al+1 … a r a_r ar的价值为
- r − l + 1 r - l + 1 r−l+1 前提是: s [ r ] − s [ l − 1 ] > 0 s[r] - s[l-1] > 0 s[r]−s[l−1]>0
- 0 0 0 前提是: s [ r ] − s [ l − 1 ] = 0 s[r] - s[l-1] = 0 s[r]−s[l−1]=0
- − ( r − l + 1 ) -(r - l +1) −(r−l+1) 前提是: s [ r ] − s [ l − 1 ] < 0 s[r] - s[l-1] < 0 s[r]−s[l−1]<0
求若干个连续的子数组的价值之和的最大值
思路:
假设 f [ i ] f[i] f[i]表示只考虑数组的前i个数的最大价值之和。
由题意得
- f [ i ] = f [ j ] + ( i − j ) , [ s [ i ] − s [ j ] > 0 , j < i ] f[i] = f[j] + (i - j) ,[s[i]-s[j]>0,j<i] f[i]=f[j]+(i−j),[s[i]−s[j]>0,j<i]
- f [ i ] = f [ j ] , [ s [ i ] − s [ j ] = 0 , j < i ] f[i] = f[j],[s[i]-s[j]=0,j<i] f[i]=f[j],[s[i]−s[j]=0,j<i]
- f [ i ] = f [ j ] − ( i − j ) , [ s [ i ] − s [ j ] < 0 , j < i ] f[i] = f[j] - (i - j) ,[s[i]-s[j]<0,j<i] f[i]=f[j]−(i−j),[s[i]−s[j]<0,j<i]
时间复杂度 O n 2 On^2 On2
考虑优化,将上述三个式子进一步化简为
- f [ i ] − i = f [ j ] − j , [ s [ i ] > s [ j ] , j < i ] f[i] -i = f[j] - j ,[s[i]>s[j],j<i] f[i]−i=f[j]−j,[s[i]>s[j],j<i]
- f [ i ] = f [ j ] , [ s [ i ] = s [ j ] , j < i ] f[i] = f[j],[s[i]=s[j],j<i] f[i]=f[j],[s[i]=s[j],j<i]
- f [ i ] + i = f [ j ] + j , [ s [ i ] < s [ j ] , j < i ] f[i] + i = f[j] + j ,[s[i]<s[j],j<i] f[i]+i=f[j]+j,[s[i]<s[j],j<i]
考虑第一个式子,
f [ i ] − i = f [ j ] − j , [ s [ i ] > s [ j ] , j < i ] f[i] -i = f[j] - j ,[s[i]>s[j],j<i] f[i]−i=f[j]−j,[s[i]>s[j],j<i]
等价于
f [ i ] = m a x ( f [ j ] − j ) + i , [ s [ j ] < s [ i ] , j < i ] f[i] = max(f[j] - j)+i,[s[j]<s[i],j<i] f[i]=max(f[j]−j)+i,[s[j]<s[i],j<i]
我们可以把所有的 s [ i ] s[i] s[i]当做数组的下标,
等价于对每一个 i i i,查询所有的小于 s [ i ] s[i] s[i]这个下标的 f [ j ] − j f[j]-j f[j]−j的最大值
考虑 s [ i ] s[i] s[i]的范围过大,无法作为数组下标,我们可以将所有的 s [ i ] s[i] s[i]离散化
然后查询所有的小于 s [ i ] s[i] s[i]这个下标的 f [ j ] − j f[j]-j f[j]−j的最大值来更新 f [ i ] f[i] f[i]
然后在这颗线段树上更新下标为 s [ i ] s[i] s[i]的值为 f [ i ] − i f[i] - i f[i]−i
第二个和第三个式子同理
我们可以建立三颗线段树,
查询区间最大值,单点修改,即可
时间复杂度: O n l o g n Onlogn Onlogn
#include <bits/stdc++.h>
#define fer(i,a,b) for(re i = a ; i <= b ; ++ i)
#define der(i,a,b) for(re i = a ; i >= b ; -- i)
#define cf int _; cin>> _; while(_--)
#define all(x) (x).begin(),(x).end()
#define sf(x) scanf("%lld",&x)
#define re register int
#define lb lower_bound
#define int long long
#define pb push_back
using namespace std;
const int N = 5e5 + 10 , M = 1e9 , mod = 1e9 + 7 ; // mod = 998244353 ;
const double eps = 1e-7 , pi = acos(-1.0) ;
int n ;
int a[N] , s[N] ;
int f[N] ;
vector<int> q ;
struct Node
{
int l, r;
int v ; // 区间[l, r]中的最大值
}tr[3][N * 4];
int d ;
int get(int x)
{
return lb(all(q) , x) - q.begin() + 1 ;
}
void pushup(int u) // 由子节点的信息,来计算父节点的信息
{
tr[d][u].v = max(tr[d][u<<1].v,tr[d][u<<1|1].v);
}
void build(int u, int l, int r)
{
if(l == r)
{
tr[d][u] = {
l,r,-M};
}
else
{
tr[d][u] = {
l,r};
int mid = r + l >> 1 ;
build(u << 1 , l , mid );
build(u << 1 | 1 , mid + 1 , r);
pushup(u) ;
}
}
int query(int u, int l, int r)
{
if(tr[d][u].l >= l && tr[d][u].r <= r)
return tr[d][u].v ;
int v = -1e9 , minv = 1e9 ;
int mid = tr[d][u].l + tr[d][u].r >> 1 ;
if(l <= mid)
{
v = max(v,query(u << 1 , l ,r)) ;
}
if(r > mid)
{
v = max(v,query(u << 1 | 1 , l , r)) ;
}
return v ;
}
void modify(int u, int x, int v)
{
if(tr[d][u].l == x && tr[d][u].r == x) tr[d][u].v = max(v , tr[d][u].v) ;
else
{
int mid = tr[d][u].l + tr[d][u].r >> 1 ;
if(x <= mid) modify(u << 1 , x , v);
else modify(u << 1 | 1 , x ,v);
pushup(u);
}
}
signed main()
{
cf
{
cin >> n ;
fer(i,1,n) sf(a[i]) , s[i] = s[i - 1] + a[i] ;
fer(i,0,n) f[i] = -1e9 ;
f[0] = 0 ;
q.clear() ;
fer(i,0,n) q.pb(s[i]) ;
sort(all(q)) ;
q.erase( unique(all(q)) , q.end() ) ;
// d=0/1/2分别表示三颗线段树
fer(i,0,2)
{
d = i ;
build(1 , 1 , n + 1) ;
}
fer(i,0,2)
{
d = i ;
modify(1 , get(s[0]) , 0) ;
}
fer(i,1,n)
{
int w = get(s[i]) ;
d = 0 ;
f[i] = query(1 , 1 , w - 1) + i ;
d = 1 ;
f[i] = max(f[i] , query( 1 , w , w ) ) ;
d = 2 ;
f[i] = max(f[i] , query( 1 , w + 1 , n + 1) - i ) ;
d = 0 ;
modify(1 , w , f[i] - i) ;
d = 1 ;
modify(1 , w , f[i]) ;
d = 2 ;
modify(1 , w , f[i] + i) ;
}
cout << f[n] << "\n" ;
}
return 0 ;
}
版权声明
本文为[ZZXzzx0_0]所创,转载请带上原文链接,感谢
https://blog.csdn.net/yueshehanjiang/article/details/124287227
边栏推荐
- Wechat applet part of the mobile phone Preview PDF did not respond
- Keysight has chosen what equipment to buy for you
- Introduction to ROS learning notes (I)
- Scrollto and scrollby
- openlayers 5.0 离散聚合点
- Client interns of a large factory share their experience face to face
- Circuit on-line simulation
- 12个例子夯实promise基础
- 開關電源設計分享及電源設計技巧圖解
- Is it safe to open an account in Bohai futures.
猜你喜欢
Simple use of navigation in jetpack
mysql_linux版本的下載及安裝詳解
开关电源设计分享及电源设计技巧图解
Redis optimization series (III) solve common problems after master-slave configuration
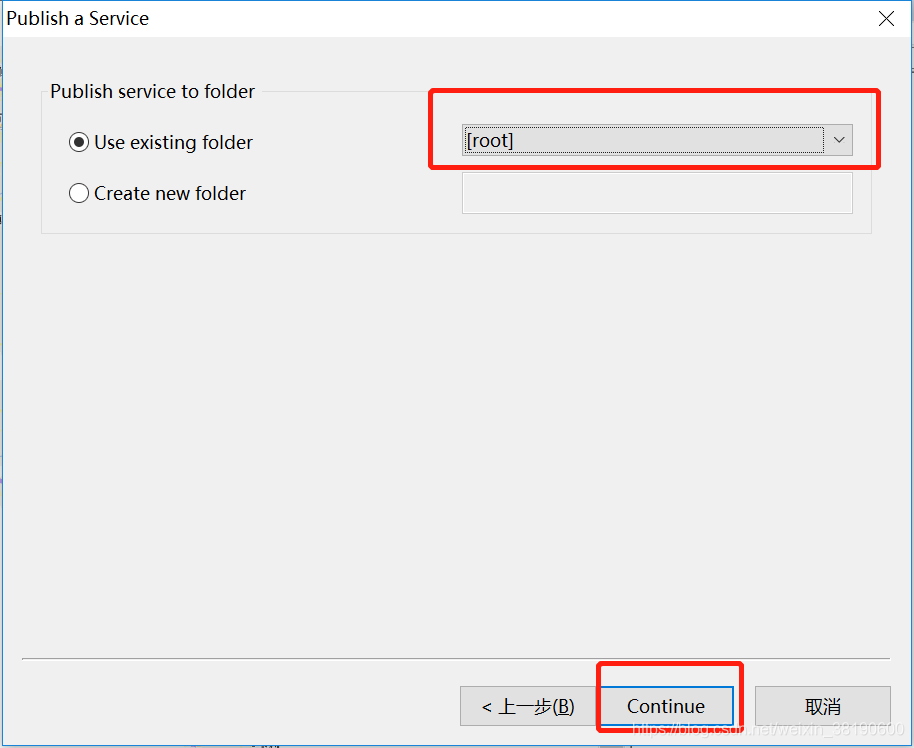
arcMap 发布切片服务
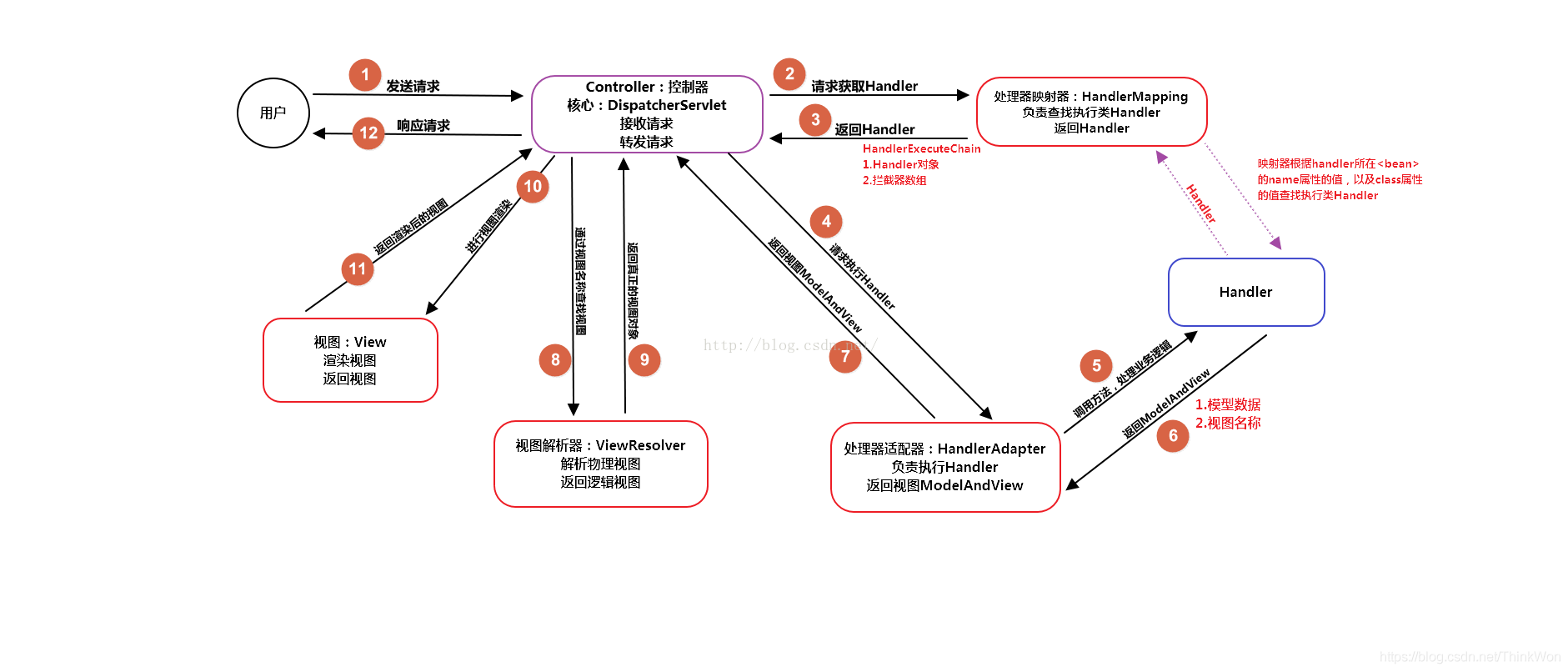
JVM的类加载过程

開關電源設計分享及電源設計技巧圖解

MVVM model

Android Development: the client obtains the latest value in the database in real time and displays it on the interface

Practice of Druid SQL and security in meituan review
随机推荐
腾讯云GPU最佳实践-使用jupyter pycharm远程开发训练
Class loading process of JVM
Dynamically add and delete layouts
OpenHarmony开源开发者成长计划,寻找改变世界的开源新生力!
Esp32 (UART event) - serial port event learning (1)
电路在线模拟
: app: transformclasseswithrobustfordevrease meituan hot repair compilation error record
SQL Server database in clause and exists clause conversion
12 examples to consolidate promise Foundation
MySQL Téléchargement et installation de la version Linux
All table queries and comment description queries of SQL Server
浅谈c语言指针的强制转换
Click the input box to pop up the keyboard layout and move up
openlayers draw矩形
Yyds dry goods inventory stringprep --- Internet string preparation
Redis common interview questions
Download xshell 6 and xftp6 official websites
Tencent map and high logo removal method
Openlayers 5.0 two centering methods
2022.04.23(LC_714_买卖股票的最佳时机含手续费)