目录

一、无约束优化

1.梯度下降法

2.牛顿法

二、有约束优化

1.约束为等式

2.约束为不等式 

一、无约束优化

无约束优化问题十分普遍，如梯度下降法、牛顿法就是无约束的优化算法。

        像最小二乘法、极大似然估计，我们都是通过求导数等于0的方式求得极值，但是有的方程求导无法取得最优解，又当如何呢？

1.梯度下降法

如下图所示，为一个二元函数，我们需要求它的最值，那么用梯度下降算法应该怎么求呢？

 随机设定一个点P，朝那个方向走会使得函数值变小呢？

        我们看下图的等高线，这个等高线是平行于xOy这个平面的，这个等高线就相当于多个横切面，等高线上的函数值是相等的。

        那往那个方向走函数值可以最快的变小呢？，如图所示的箭头为梯度的方向，梯度的方向即增长最快的方向，而我们希望函数值最快的减小，则P应该朝着梯度的反方向移动。

那么，为什么向着梯度的负方向下降最快呢？

 假设f(x)是一个n维的函数，f 是个标量，它的梯度是对各个维度求偏导。

假设原始定义的P点为 ，假设每次移动的步幅为L，假设移动的方向为θ，则得到它移动后的位置为P'，则P-P' 之间的长度为L，PP'与x轴之间的夹角为θ，则P'的坐标为 

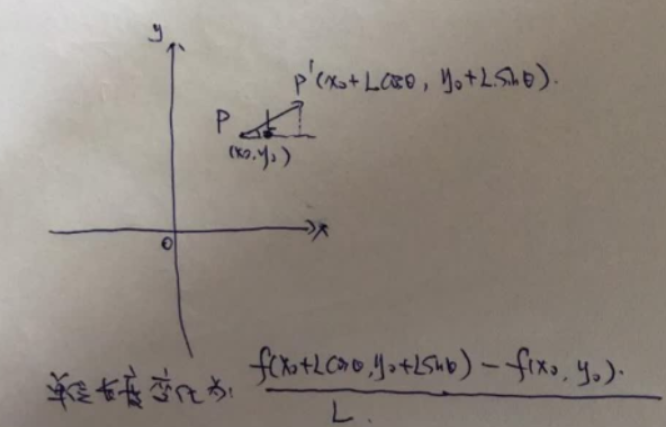
其移动的变化量为：

则其单位长度变化为：

我们对这个函数进行变换：

        第二行对第一行的式子减了一个，又加了一个，等于没变；然后第三行对第二行进行变换，左式分子分母同时乘sinθ，右式分子分母同时乘cosθ，结果保持不变；当L→0时，即移动的步幅很小，那第三个式子就可以变为,其中和分别为对x，y的偏导。

那么该式就只与θ有关。

        我们想要计算最大梯度，也就是计算单位长度变化大的方向，即求得一个θ，使单位长度变化最大。

        我们对进行一个变换。如下图所示：

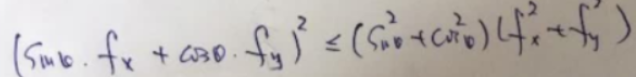
这个结果是怎么来的呢？

参考：柯西不等式 

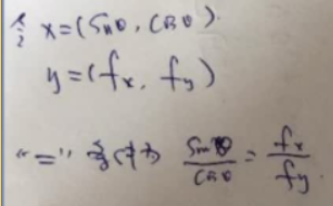
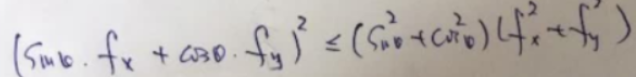
什么时候等号成立呢？cosθ=1时，即θ=0时，也就是两个向量同向的时候，即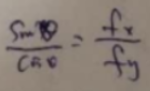，这样就可以算出θ值了，这个θ值就是梯度的方向。

这就说明了为什么沿着最大梯度的反方向下降最快。

2.牛顿法

下面用两种方法来解释牛顿法，我们的目标都是使f(x)最小。

（1）方法一

我们假设一个函数g(x)，我们想一步一步的降低g(x)，使之最小，那牛顿法怎么做呢？

随意定义一个点，我们想求下一个更小的点，则求在的切线，该切线与x轴的交点要比更接近最小值。

我们定义了切线：

当y=0时，就是切线与x轴的角点，则得到点

（2）方法二

找到一个二次函数在相切，那这个抛物线怎么求呢？

泰勒展开式：

保留前三项即为所求的二次函数。

我们要求f(x)的最小值，就可以用这个二次函数的最小点来逼近原始函数的最小点，原理与方法一相同。

收敛速度

二、有约束优化

1.约束为等式

如下是一个等式约束的最优化问题，在g(x)=0的条件下，求f(x)的最小值。

下图坐标系中的虚线表示f(x)的等高线，要使f(x)既要满足在g(x)这条曲线上，又要满足这个椭圆的等高线最小，即曲线与椭圆相切的点为最优点，二者的梯度方向是相反的（即 λ <0）。

我们引入拉格朗日函数进行计算：

该函数分别对 x 和 λ 求导使之为0得到两个方程式：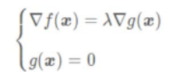

2.约束为不等式 

如下是一个约束为不等式的例子：

圆圈为f(x,y)的等高线，此时的约束为g(x,y)小于等于0，阴影为其约束范围。

当g(x)小于0时，要使得，则λ=0，此时的就不起作用了，当g(x,y)=0时，即f(x,y)的最优值在g(x,y)的领界上，λ不等于0，那么这个约束就起作用了。

我们引入拉格朗日函数得到两个公式：

注意不对  λg(x) 求导，直接让λg(x)=0，这个条件就是KKT条件，λ=0，则约束项不起作用，

看一个例子：

当求解出的x带入g(x)中，发现g(x)是大于0的，则该x点对于g(x)来说是不起作用的。

注意此处的λ>=0，因为f(x)和g(x)的梯度是相反的。

再看一个例子：