当前位置:网站首页>积性函数前缀和——杜教筛
积性函数前缀和——杜教筛
2022-04-23 06:21:00 【Zimba_】
背景:
这课太无聊了,太吵学不进去,干脆写博客好了。
题目:
给定一个 n n n,求 ∑ i = 1 n μ ( i ) \sum_{i=1}^{n}\mu(i) ∑i=1nμ(i)和 ∑ i = 1 n φ ( i ) \sum_{i=1}^{n}\varphi(i) ∑i=1nφ(i)。
( 1 ≤ n ≤ 1 0 10 ) (1\leq n\leq 10^{10}) (1≤n≤1010)
(某些积性函数前缀和)
引言:
如果不知道什么是积性函数出门左转隔壁教室。
我们知道, μ \mu μ函数和 φ \varphi φ可以 o ( n ) o(\sqrt{n}) o(n)求单点的值。
也可以用线性筛 o ( n ) o(n) o(n)预处理出多点的值。
但是显然都不够用来做这个题。
那么神奇的地方来了,这些积性函数竟然有亚线性算法求出前缀和,可能这就是数学的魅力吧。
这里我们介绍其中一个方法,杜教筛,它可以在 o ( n 3 4 ) o(n^{\frac{3}{4}}) o(n43)的复杂度内求出积性函数的前缀和。并且我们可以预处理出前 1 0 6 10^6 106个前缀和,将它的复杂度优化到 o ( n 2 3 ) o(n^{\frac{2}{3}}) o(n32)。
正文:杜教筛
假定我们要求前缀和的函数是 f f f,并令它的前缀和 S ( n ) = ∑ i = 1 n f ( i ) S(n)=\sum_{i=1}^{n}f(i) S(n)=∑i=1nf(i)。
我们找另一个函数 g g g跟它卷积求前缀和。
∑ i = 1 n ( f ∗ g ) ( i ) = ∑ i = 1 n ∑ d ∣ i g ( d ) f ( i d ) \sum_{i=1}^{n}(f*g)(i)=\sum_{i=1}^{n}\sum_{d|i}g(d)f(\frac{i}{d}) ∑i=1n(f∗g)(i)=∑i=1n∑d∣ig(d)f(di)
= ∑ d = 1 n g ( d ) ∑ i = 1 ⌊ n d ⌋ f ( i ) =\sum_{d=1}^{n}g(d)\sum_{i=1}^{\lfloor \frac{n}{d} \rfloor}f(i) =∑d=1ng(d)∑i=1⌊dn⌋f(i)
= ∑ d = 1 n g ( d ) S ( ⌊ n d ⌋ ) =\sum_{d=1}^{n}g(d)S(\lfloor \frac{n}{d} \rfloor) =∑d=1ng(d)S(⌊dn⌋)
推到这里,我们发现后面这是一个明显的数论分块式子。
但是这个式子里没有 S ( n ) S(n) S(n)呀,没 S ( n ) S(n) S(n)我们求啥。
所以现在我们要把 S ( n ) S(n) S(n)弄出来。
我们发现当 d = 1 d=1 d=1时,后面这个东西 g ( 1 ) S ( ⌊ n 1 ⌋ ) = S ( n ) g(1)S(\lfloor \frac{n}{1} \rfloor)=S(n) g(1)S(⌊1n⌋)=S(n)
然后 S ( n ) S(n) S(n)就来了。
S ( n ) = ∑ d = 1 n g ( d ) S ( ⌊ n d ⌋ ) − ∑ d = 2 n g ( d ) S ( ⌊ n d ⌋ ) S(n)=\sum_{d=1}^{n}g(d)S(\lfloor \frac{n}{d} \rfloor)-\sum_{d=2}^{n}g(d)S(\lfloor \frac{n}{d} \rfloor) S(n)=∑d=1ng(d)S(⌊dn⌋)−∑d=2ng(d)S(⌊dn⌋)
= ∑ i = 1 n ( f ∗ g ) ( i ) − ∑ d = 2 n g ( d ) S ( ⌊ n d ⌋ ) =\sum_{i=1}^{n}(f*g)(i)-\sum_{d=2}^{n}g(d)S(\lfloor \frac{n}{d} \rfloor) =∑i=1n(f∗g)(i)−∑d=2ng(d)S(⌊dn⌋)
那么后面这个式子还是一个数论分块的式子,只要我们可以快速求出 g g g的前缀和,就可以快速地求出来。
所以我们需要找到一个 g g g,使得 g g g和 f ∗ g f*g f∗g的前缀和都好求。
我们现在算一下复杂度,假设 g g g和 f ∗ g f*g f∗g的前缀和都可以 o ( 1 ) o(1) o(1)求出。 打扰了 ,反正复杂度是 o ( n 3 4 ) o(n^{\frac{3}{4}}) o(n43),如果我们预处理出前 1 0 6 10^6 106项,然后再加个记忆化,复杂度就变成 o ( n 2 3 ) o(n^{\frac{2}{3}}) o(n32)了。
那么有.
代码略了,请读者自行编写过题。
例题1:求 ∑ i = 1 n μ ( i ) \sum_{i=1}^{n}\mu(i) ∑i=1nμ(i)。
当我们考虑用杜教筛求解积性函数前缀和时,主要就是找一个 g g g使得 g g g和 f ∗ g f*g f∗g的前缀和好求。
那么对于莫比乌斯函数 μ \mu μ,我们毫无疑问是选择用 1 1 1函数。
有 μ ∗ 1 = e \mu *1=e μ∗1=e。
那么 1 1 1函数和 e e e函数的前缀和就不用多说什么了。
理A。
例题2:求 ∑ i = 1 n φ ( i ) \sum_{i=1}^{n}\varphi(i) ∑i=1nφ(i)。
g g g仍选择用 1 1 1函数,有 φ ∗ 1 = i d \varphi *1=id φ∗1=id。
那么 1 1 1函数和 i d id id函数的前缀和也很好求。
例题3:求 ∑ i = 1 n i φ ( i ) \sum_{i=1}^{n}i\varphi(i) ∑i=1niφ(i)。
我们选用 i d id id作为 g g g函数,首先 i d id id函数的前缀和可以求。
∑ i = 1 n ( f ∗ i d ) ( i ) = ∑ i = 1 n ∑ d ∣ i d φ ( d ) ∗ i d = ∑ i = 1 n i ∑ d ∣ i φ ( d ) = ∑ i = 1 n i 2 \sum_{i=1}^{n}(f*id)(i)=\sum_{i=1}^{n}\sum_{d|i}d\varphi(d)*\frac{i}{d}=\sum_{i=1}^{n}i\sum_{d|i}\varphi(d)=\sum_{i=1}^{n}i^{2} ∑i=1n(f∗id)(i)=∑i=1n∑d∣idφ(d)∗di=∑i=1ni∑d∣iφ(d)=∑i=1ni2。
其中,因为 1 ∗ φ = i d 1*\varphi =id 1∗φ=id,所以 ∑ d ∣ i φ ( d ) = i \sum_{d|i}\varphi(d)=i ∑d∣iφ(d)=i。
例题n+2:求 ∑ i = 1 n i n φ ( i ) \sum_{i=1}^{n}i^{n}\varphi(i) ∑i=1ninφ(i)。
我们选用 i d n id^{n} idn作为 g g g函数,那么 i d n id^{n} idn的前缀和可以求。(拉格朗日插值?)
∑ i = 1 n ( f ∗ i d ) ( i ) = ∑ i = 1 n ∑ d ∣ i d n φ ( d ) ∗ ( i d ) n = ∑ i = 1 n i n ∑ d ∣ i φ ( d ) = ∑ i = 1 n i n + 1 \sum_{i=1}^{n}(f*id)(i)=\sum_{i=1}^{n}\sum_{d|i}d^{n}\varphi(d)*(\frac{i}{d})^{n}=\sum_{i=1}^{n}i^{n}\sum_{d|i}\varphi(d)=\sum_{i=1}^{n}i^{n+1} ∑i=1n(f∗id)(i)=∑i=1n∑d∣idnφ(d)∗(di)n=∑i=1nin∑d∣iφ(d)=∑i=1nin+1。
暂时我知道就上面这些吧。
版权声明
本文为[Zimba_]所创,转载请带上原文链接,感谢
https://blog.csdn.net/weixin_43785386/article/details/108873041
边栏推荐
- 城市应急管理|城市突发事故应急通信指挥调度系统
- 技术小白的第一篇(表达自己)
- USO technology was invited to share the technical framework and challenges of AI synthetic virtual characters at lvson2020 conference
- 组合数求解与(扩展)卢卡斯定理
- 免费开源智能充电桩物联网SAAS云平台
- presto日期函数的使用
- 菜菜的并发编程笔记 |(五)线程安全问题以及Lock解决方案
- 菜菜的并发编程笔记 |(九)异步IO实现并发爬虫加速
- 记录一下使用v-print中遇到的问题
- 免费开源农业物联网云平台(Version:3.0.1)
猜你喜欢

quill-editor图片缩放、在一个页面使用多个富文本框、quill-editor上传图片地址为服务器地址

可视化常见问题解决方案(九)背景颜色问题

el-select 中v-model绑定值,数据回显只显示value,不显示label

How to improve the service efficiency of the hotel without blind spots and long endurance | public and Private Integrated walkie talkie?
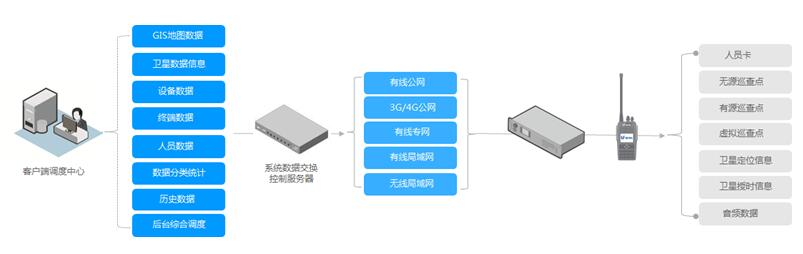
南方投资大厦SDC智能通信巡更管理系统

H5案例开发

不需要破解markdown编辑工具Typora

电力行业巡检对讲通信系统

Us photo cloud editing helps BiliBili upgrade its experience

可视化之路(十二)Collection类详解
随机推荐
HQL语句的调优
PC端一次启动多个微信
MVCC(多版本并发控制)
golang实现一个带Web界面的五险一金计算器
ESP32学习-向工程项目添加文件夹
Meishe technology launches professional video editing solution for desktop -- Meiying PC version
各类日期转化的utils
Us photo cloud editing helps BiliBili upgrade its experience
Machine vision series (01) -- Overview
Machine vision series (02) -- tensorflow2 3 + win10 + GPU installation
记录一下使用v-print中遇到的问题
Solution of emergency communication system for major security incidents
学习笔记5-梯度爆炸和梯度消失(K折交叉验证)
SQL练习第一题
go iris框架实现多服务Demo:通过(监听8083端口的)服务1中的接口启动(监听8084端口的)服务2
Take you to travel in space, and American photography technology provides comprehensive technical support for aerospace creative applet
VScode
Object. Create() principle, object Create() specification, handwritten object create(),Object. Create() usage
PyTorch 13. Nested functions and closures (dog head)
Mysql持久性的实现