当前位置:网站首页>BP神经网络
BP神经网络
2022-08-08 18:28:00 【立志变强的学生】
讲解视频:学习视频
B P BP BP神经网络
1.激活函数
激活函数(Activation Function)是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。激活函数对于人工神经网络模型去学习、理解复杂的非线性函数,具有十分重要的作用。
如果不使用激活函数,每一层输出都是上一层输入的线性运算,无论神经网络有多少层,最终的输出只是输入的线性组合,相当于感知机。如果使用了激活函数,将非线性因素引入到网络中,使得神经网络可以任意逼近任何非线性函数,能够应用到更多的非线性模型。
常用的激活函数
s i g m o i d sigmoid sigmoid 函数
S i g m o i d Sigmoid Sigmoid函数是一个在生物学中常见的S型函数,也称为S型生长曲线。在信息科学中,由于其单增以及反函数单增等性质,Sigmoid函数常被用作神经网络的阈值函数,将变量映射到0,1之间,公式如下:
f ( x ) = 1 1 + e ( − x ) f(x)=\frac{1}{1+e^{(-x)}} f(x)=1+e(−x)1
R e L U ReLU ReLU函数
R e l u Relu Relu激活函数(The Rectified Linear Unit),用于隐藏层的神经元输出。公式如下:
f ( x ) = m a x ( 0 , x ) f(x)=max(0,x) f(x)=max(0,x)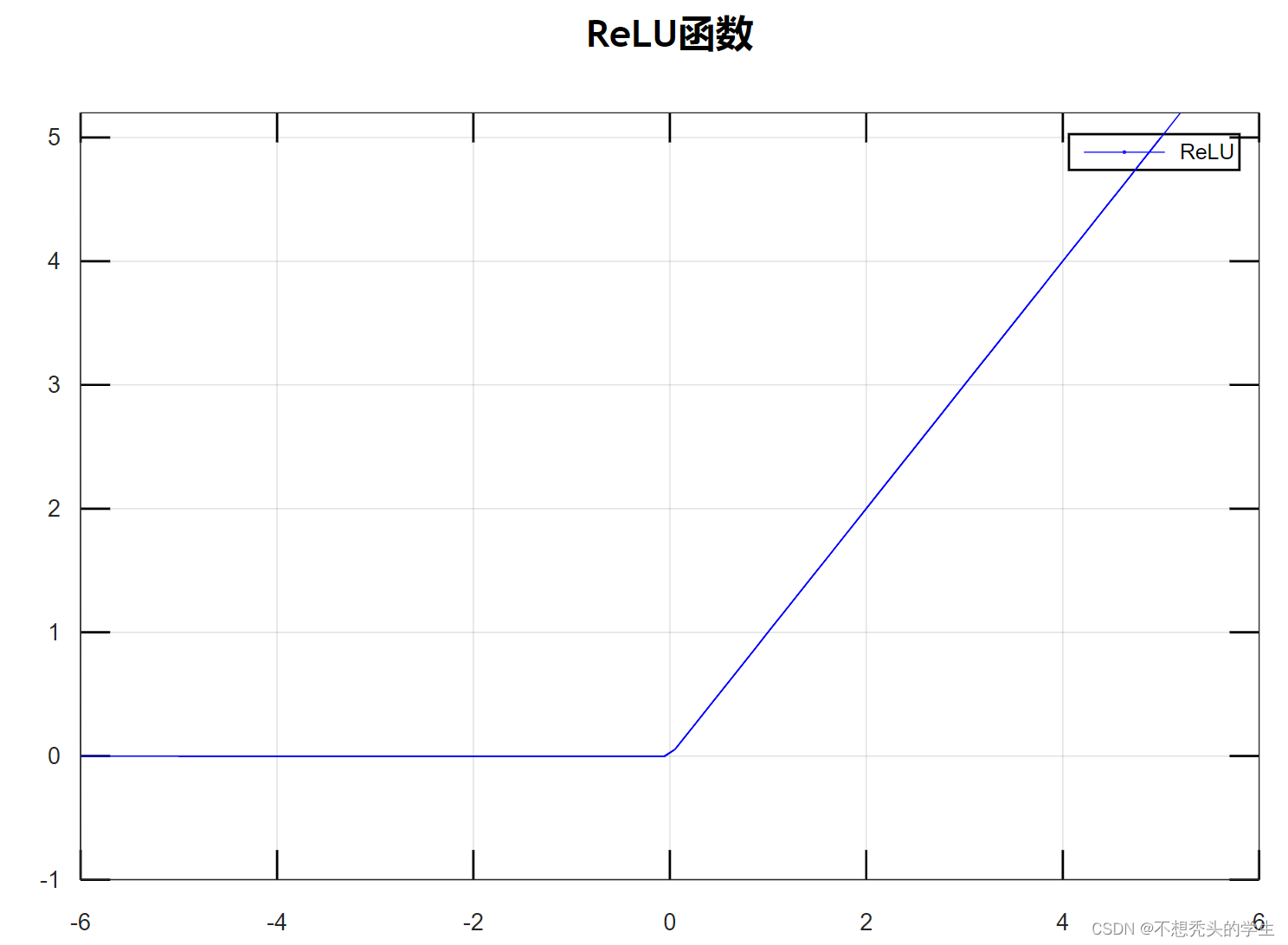
T a n h Tanh Tanh 函数
T a n h Tanh Tanh 是双曲函数中的一个, T a n h ( ) Tanh() Tanh() 为双曲正切。在数学中,双曲正切“ T a n h Tanh Tanh”是由基本双曲函数双曲正弦和双曲余弦推导而来。公式如下:
f ( x ) = e x − e − x e x + e − x f(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} f(x)=ex+e−xex−e−x
s o f t m a x softmax softmax 函数
s o f t m a x softmax softmax 函数用于输出层。假设输出层共有 n n n 个神经元,计算第 k k k 个神经元的输出 y k y_k yk。 s o f t m a x softmax softmax 函数的分子是输入信号 a k a_k ak 的指数函数,分母是所有输入信号的指数函数的和。 s o f t m a x softmax softmax 函数公式如下:
y k = e a k ∑ i = 1 n e a i y_{k}=\frac{e^{a_{k}}}{\sum_{i=1}^{n} e^{a_{i}}} yk=∑i=1neaieak
2.神经网络结构
第0层是输入层(2个神经元),第1层是隐含层(3个神经元),第2层是隐含层(2个神经元),第3层是输出层。

符号约定
w j k [ l ] w_{j k}^{[l]} wjk[l]表示从网络第 ( l − 1 ) t h (l-1)^{t h} (l−1)th 层第 k t h k^{t h} kth 个神经元指向第 l t h l^{t h} lth 层第 j t h j^{t h} jth 个神经元的连接权重,同时也是第 l l l 层权重矩阵第 j j j 行第 k k k 列的元素。例如,上图中 w 21 [ 1 ] w_{21}^{[1]} w21[1] ,第0层第1个神经元指向第1层第2个神经元的权重(褐色),也就是第 1 层权重矩阵第 2 行第 1 列的元素。同理,使用 b j [ l ] b_{j}^{[l]} bj[l] 表示第 l t h l^{t h} lth 层第 j t h j^{t h} jth 个神经元的偏置 ,同时也是第 l l l 层偏置向量的第 j j j 个元素。使用 z j [ l ] z_{j}^{[l]} zj[l] 表示第 l t h l^{t h} lth 层第 j t h j^{t h} jth 个神经元的线性结果,使用 a j [ l ] a_{j}^{[l]} aj[l] 来表示第 l t h l^{t h} lth 层第 j t h j^{t h} jth 个神经元的激活函数输出。其中,激活函数使用符号σ表示,第 l t h l^{t h} lth 层中第 j t h j^{t h} jth 个神经元的激活为:
a j [ l ] = σ ( z j [ l ] ) = σ ( ∑ k w j k [ l ] a k [ l − 1 ] + b j [ l ] ) a_{j}^{[l]}=\sigma(z_{j}^{[l]})=\sigma\left(\sum_{k} w_{j k}^{[l]} a_{k}^{[l-1]}+b_{j}^{[l]}\right) aj[l]=σ(zj[l])=σ(k∑wjk[l]ak[l−1]+bj[l])
w [ l ] w^{[l]} w[l] 表示第 l l l 层的权重矩阵, b [ l ] b^{[l]} b[l] 表示第 l l l 层的偏置向量, a [ l ] a^{[l]} a[l] 表示第 l l l 层的神经元向量,结合上图讲述:
w [ 1 ] = [ w 11 [ 1 ] w 12 [ 1 ] w 21 [ 1 ] w 22 [ 1 ] w 31 [ 1 ] w 32 [ 1 ] ] w^{[1]}=\left[\begin{array}{lll}w_{11}^{[1]} & w_{12}^{[1]} & \\ w_{21}^{[1]} & w_{22}^{[1]} & \\ w_{31}^{[1]} & w_{32}^{[1]}\end{array}\right] w[1]=⎣⎡w11[1]w21[1]w31[1]w12[1]w22[1]w32[1]⎦⎤ w [ 2 ] = [ w 11 [ 2 ] w 12 [ 2 ] w 13 [ 2 ] w 21 [ 2 ] w 22 [ 2 ] w 23 [ 2 ] ] w^{[2]}=\left[\begin{array}{lll}w_{11}^{[2]} & w_{12}^{[2]} & w_{13}^{[2]} \\ w_{21}^{[2]} & w_{22}^{[2]} & w_{23}^{[2]}\end{array}\right] w[2]=[w11[2]w21[2]w12[2]w22[2]w13[2]w23[2]]
b [ 1 ] = [ b 1 [ 1 ] b 2 [ 1 ] b 3 [ 1 ] ] b^{[1]}=\left[\begin{array}{l}b_{1}^{[1]} \\ b_{2}^{[1]} \\ b_{3}^{[1]}\end{array}\right] b[1]=⎣⎡b1[1]b2[1]b3[1]⎦⎤ b [ 2 ] = [ b 1 [ 2 ] b 2 [ 2 ] ] b^{[2]}=\left[\begin{array}{l}b_{1}^{[2]} \\ b_{2}^{[2]}\end{array}\right] b[2]=[b1[2]b2[2]]
进行线性矩阵运算。
z [ 1 ] = [ w 11 [ 1 ] w 12 [ 1 ] w 21 [ 1 ] w 22 [ 1 ] w 31 [ 1 ] w 32 [ 1 ] ] ⋅ [ a 1 [ 0 ] a 2 [ 0 ] ] + [ b 1 [ 1 ] b 2 [ 1 ] b 3 [ 1 ] ] = [ w 11 [ 1 ] a 1 [ 0 ] + w 12 [ 1 ] a 2 [ 0 ] + b 1 [ 1 ] w 21 [ 1 ] a 1 [ 0 ] + w 22 [ 1 ] a 2 [ 0 ] + b 2 [ 1 ] w 31 [ 1 ] a 1 [ 0 ] + w 32 [ 1 ] a 2 [ 0 ] + b 3 [ 1 ] ] z^{[1]}=\left[\begin{array}{lll}w_{11}^{[1]} & w_{12}^{[1]} & \\ w_{21}^{[1]} & w_{22}^{[1]} & \\ w_{31}^{[1]} & w_{32}^{[1]}\end{array}\right] \cdot\left[\begin{array}{c}a_{1}^{[0]} \\ a_{2}^{[0]}\end{array}\right]+\left[\begin{array}{l}b_{1}^{[1]} \\ b_{2}^{[1]} \\ b_{3}^{[1]}\end{array}\right]=\left[\begin{array}{c}w_{11}^{[1]} a_{1}^{[0]}+w_{12}^{[1]} a_{2}^{[0]}+b_{1}^{[1]} \\ w_{21}^{[1]} a_{1}^{[0]}+w_{22}^{[1]}a_{2}^{[0]}+b_{2}^{[1]} \\ w_{31}^{[1]}a_{1}^{[0]}+w_{32}^{[1]}a_{2}^{[0]}+b_{3}^{[1]}\end{array}\right] z[1]=⎣⎡w11[1]w21[1]w31[1]w12[1]w22[1]w32[1]⎦⎤⋅[a1[0]a2[0]]+⎣⎡b1[1]b2[1]b3[1]⎦⎤=⎣⎡w11[1]a1[0]+w12[1]a2[0]+b1[1]w21[1]a1[0]+w22[1]a2[0]+b2[1]w31[1]a1[0]+w32[1]a2[0]+b3[1]⎦⎤
矩阵形状 (3,2) (2,1) (3,1) (3,1)
z [ 2 ] = [ w 11 [ 2 ] w 12 [ 2 ] w 13 [ 2 ] w 21 [ 2 ] w 22 [ 2 ] w 23 [ 2 ] ] ⋅ [ a 1 [ 1 ] a 2 [ 1 ] a 3 [ 1 ] ] + [ b 1 [ 2 ] b 2 [ 2 ] ] = [ w 11 [ 2 ] a 1 [ 1 ] + w 12 [ 2 ] a 2 [ 1 ] + w 13 [ 2 ] a 3 [ 1 ] + b 1 [ 2 ] w 21 [ 2 ] a 1 [ 1 ] + w 22 [ 2 ] a 2 [ 1 ] + w 23 [ 2 ] a 3 [ 1 ] + b 2 [ 2 ] ] z^{[2]}=\left[\begin{array}{ccc}w_{11}^{[2]} & w_{12}^{[2]} & w_{13}^{[2]} \\ w_{21}^{[2]} & w_{22}^{[2]} & w_{23}^{[2]}\end{array}\right] \cdot\left[\begin{array}{c}a_{1}^{[1]} \\ a_{2}^{[1]} \\ a_{3}^{[1]}\end{array}\right]+\left[\begin{array}{c}b_{1}^{[2]} \\ b_{2}^{[2]}\end{array}\right]=\left[\begin{array}{c}w_{11}^{[2]} a_{1}^{[1]}+w_{12}^{[2]} a_{2}^{[1]}+w_{13}^{[2]} a_{3}^{[1]}+b_{1}^{[2]} \\ w_{21}^{[2]} a_{1}^{[1]}+w_{22}^{[2]} a_{2}^{[1]}+w_{23}^{[2]} a_{3}^{[1]}+b_{2}^{[2]}\end{array}\right] z[2]=[w11[2]w21[2]w12[2]w22[2]w13[2]w23[2]]⋅⎣⎡a1[1]a2[1]a3[1]⎦⎤+[b1[2]b2[2]]=[w11[2]a1[1]+w12[2]a2[1]+w13[2]a3[1]+b1[2]w21[2]a1[1]+w22[2]a2[1]+w23[2]a3[1]+b2[2]]
矩阵形状 (2,3) (3,1) (2,1) (2,1)
那么,前向传播过程可以表示为:
a [ l ] = σ ( w [ l ] a [ l − 1 ] + b [ l ] ) a^{[l]}=\sigma\left(w^{[l]} a^{[l-1]}+b^{[l]}\right) a[l]=σ(w[l]a[l−1]+b[l])
上述讲述的前向传播过程,输入层只有1个列向量,也就是只有一个输入样本。对于多个样本,输入不再是1个列向量,而是m个列向量,每1列表示一个输入样本。m个 a [ l − 1 ] a^{[l-1]} a[l−1]列向量组成一个m列的矩阵 A [ l − 1 ] A^{[l-1]} A[l−1]。
A [ l − 1 ] = [ ∣ ∣ ⋯ ∣ a [ l − 1 ] ( 1 ) a [ l − 1 ] ( 2 ) … a [ l − 1 ] ( m ) ∣ ∣ … ∣ ] A^{[l-1]}=\left[\begin{array}{cccc}| & | & \cdots & | \\ a^{[l-1](1)} & a^{[l-1](2)} & \dots & a^{[l-1](m)} \\ | & | & \dots & |\end{array}\right] A[l−1]=⎣⎡∣a[l−1](1)∣∣a[l−1](2)∣⋯……∣a[l−1](m)∣⎦⎤
多样本输入的前向传播过程可以表示为:
Z [ l ] = w [ l ] ⋅ A [ l − 1 ] + b [ l ] A [ l ] = σ ( Z [ l ] ) \begin{array}{c} Z^{[l]}=w^{[l]} \cdot A^{[l-1]}+b^{[l]} \\ A^{[l]}=\sigma\left(Z^{[l]}\right) \end{array} Z[l]=w[l]⋅A[l−1]+b[l]A[l]=σ(Z[l])
与单样本输入相比,多样本 w [ l ] w^{[l]} w[l]和 b [ l ] b^{[l]} b[l]的定义是完全一样的,不同的只是 Z [ l ] Z^{[l]} Z[l]和 A [ l ] A^{[l]} A[l]从1列变成m列,每1列表示一个样本的计算结果。
3.损失函数
在有监督的机器学习算法中,我们希望在学习过程中最小化每个训练样例的误差。通过梯度下降等优化策略完成的,而这个误差来自损失函数。
损失函数用于单个训练样本,而成本函数是多个训练样本的平均损失。优化策略旨在最小化成本函数。下面例举几个常用的损失函数。
回归问题
- 绝对值损失函数( L 1 L_{1} L1损失函数):
L ( y ^ , y ) = ∣ y − y ^ ∣ L(\hat{y},y)=|y-\hat{y}| L(y^,y)=∣y−y^∣
y y y 表示真实值或期望值, y ^ \hat{y} y^ 表示预测值
- 平方损失函数( L 2 L_{2} L2损失函数):
L ( y ^ , y ) = ( y − y ^ ) 2 L(\hat{y},y)=(y-\hat{y})^{2} L(y^,y)=(y−y^)2
y y y 表示真实值或期望值, y ^ \hat{y} y^ 表示预测值
分类问题
- 交叉熵损失:
L ( y ^ , y ) = − y log ( y ^ ) − ( 1 − y ) log ( 1 − y ^ ) L(\hat{y}, y)=-y \log (\hat{y})-(1-y) \log (1-\hat{y}) L(y^,y)=−ylog(y^)−(1−y)log(1−y^)
y y y 表示真实值或期望值, y ^ \hat{y} y^ 表示预测值
4.反向传播
反向传播的基本思想:通过计算输出层与期望值之间的误差来调整网络参数,使得误差变小(最小化损失函数或成本函数)。反向传播基于四个基础等式,非常简洁优美,但想要理解透彻还是挺烧脑的。
求解梯度矩阵
假设函数 f : R n × 1 → R f:R^{n \times 1} \rightarrow R f:Rn×1→R 将输入的列向量(shape: n × 1 n \times 1 n×1 )映射为一个实数。那么,函数 f f f 的梯度定义为:
∇ x f ( x ) = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋮ ∂ f ( x ) ∂ x n ] \nabla_{x} f(x)=\left[\begin{array}{c}\frac{\partial f(x)}{\partial x_{1}} \\ \frac{\partial f(x)}{\partial x_{2}} \\ \vdots \\ \frac{\partial f(x)}{\partial x_{n}}\end{array}\right] ∇xf(x)=⎣⎡∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x)⎦⎤
同理,假设函数 f : R m × n → R f: R^{m \times n} \rightarrow R f:Rm×n→R 将输入的矩阵(shape: m × n m \times n m×n )映射为一个实数。函数 f f f 的梯度定义为:
∇ A f ( A ) = [ ∂ f ( A ) ∂ A 11 ∂ f ( A ) ∂ A 12 … ∂ f ( A ) ∂ A 13 ∂ f ( A ) ∂ A 21 ∂ f ( A ) ∂ A 22 … ∂ f ( A ) ∂ A 2 n ⋮ ⋮ ⋱ ⋮ ∂ f ( A ) ∂ A m 1 ∂ f ( A ) ∂ A m 2 … ∂ f ( A ) ∂ A m n ] \nabla_{A} f(A)=\left[\begin{array}{cccc}\frac{\partial f(A)}{\partial A_{11}} & \frac{\partial f(A)}{\partial A_{12}} & \dots & \frac{\partial f(A)}{\partial A_{13}} \\ \frac{\partial f(A)}{\partial A_{21}} & \frac{\partial f(A)}{\partial A_{22}} & \dots & \frac{\partial f(A)}{\partial A_{2 n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f(A)}{\partial A_{m 1}} & \frac{\partial f(A)}{\partial A_{m 2}} & \dots & \frac{\partial f(A)}{\partial A_{m n}}\end{array}\right] ∇Af(A)=⎣⎡∂A11∂f(A)∂A21∂f(A)⋮∂Am1∂f(A)∂A12∂f(A)∂A22∂f(A)⋮∂Am2∂f(A)……⋱…∂A13∂f(A)∂A2n∂f(A)⋮∂Amn∂f(A)⎦⎤
可以简化为:
( ∇ A f ( A ) ) i j = ∂ f ( A ) ∂ A i j \left(\nabla_{A} f(A)\right)_{i j}=\frac{\partial f(A)}{\partial A_{i j}} (∇Af(A))ij=∂Aij∂f(A)
注意:梯度求解的前提是函数 f f f 返回的必须是一个实数,如果函数返回的是一个矩阵或者向量,是没有办法求解梯度的。例如,函数 f ( A ) = ∑ i = 0 m ∑ j = 0 n A i j 2 f(A) =\sum_{i=0}^{m} \sum_{j=0}^{n} A_{i j}^{2} f(A)=∑i=0m∑j=0nAij2,函数返回一个实数,可以求解梯度矩阵。如果 f ( x ) = A x ( A ∈ R m × n , x ∈ R n × 1 ) , f(x)=A x\left(A \in R^{m \times n}, x \in R^{n \times 1}\right), f(x)=Ax(A∈Rm×n,x∈Rn×1), 函数返回一个m行的列向量,就不能对 f f f 求解梯度矩阵。
矩阵相乘
矩阵 A = [ 1 2 3 4 ] A=\left[\begin{array}{cc}1 & 2 \\ 3 & 4\end{array}\right] A=[1324],矩阵 B = [ − 1 − 2 − 3 − 4 ] B=\left[\begin{array}{cc}-1 & -2 \\ -3 & -4\end{array}\right] B=[−1−3−2−4]
A B = [ 1 × − 1 + 2 × − 3 1 × − 2 + 2 × − 4 3 × − 1 + 4 × − 3 3 × − 2 + 4 × − 4 ] = [ − 7 − 10 − 15 − 22 ] A B=\left[\begin{array}{ll}1 \times-1+2 \times-3 & 1 \times-2+2 \times-4 \\ 3 \times-1+4 \times-3 & 3 \times-2+4 \times-4\end{array}\right]=\left[\begin{array}{cc}-7 & -10 \\ -15 & -22\end{array}\right] AB=[1×−1+2×−33×−1+4×−31×−2+2×−43×−2+4×−4]=[−7−15−10−22]
矩阵对应元素相乘
使用符号 ⊙ \odot ⊙表示:
A ⊙ B = [ 1 × − 1 2 × − 2 3 × − 3 4 × − 4 ] = [ − 1 − 4 − 9 − 16 ] A \odot B=\left[\begin{array}{cc}1 \times-1 & 2 \times-2 \\ 3 \times-3 & 4 \times-4\end{array}\right]=\left[\begin{array}{cc}-1 & -4 \\ -9 & -16\end{array}\right] A⊙B=[1×−13×−32×−24×−4]=[−1−9−4−16]
梯度下降法
从几何意义,梯度矩阵代表了函数增加最快的方向,沿着梯度相反的方向可以更快找到最小值。

反向传播的过程就是利用梯度下降法原理,逐步找到成本函数的最小值,得到最终的模型参数。
反向传播公式推导(四个基础等式)
要想最小化成本函数,需要求解神经网络中的权重 w w w 和偏置 b b b 的梯度,再用梯度下降法优化参数。求解梯度也就是计算偏导数 ∂ L ( a [ l ] , y ) ∂ w j k [ l ] \frac{\partial L\left(a^{[l]}, y\right)}{\partial w_{j k}^{[l]}} ∂wjk[l]∂L(a[l],y) 和 ∂ L ( a [ l ] , y ) ∂ b j [ l ] \frac{\partial L\left(a^{[l]}, y\right)}{\partial b_{j}^{[l]}} ∂bj[l]∂L(a[l],y) 。为了计算这些偏导数,引入一个中间变量 δ j [ l ] \delta_{j}^{[l]} δj[l],它表示网络中第 l t h l^{t h} lth 层第 j t h j^{t h} jth 个神经元的误差。反向传播能够计算出误差 δ j [ l ] , \delta_{j}^{[l]}, δj[l], 再根据链式法则求出 ∂ L ( a [ l ] , y ) ∂ w j k [ l ] \frac{\partial L\left(a^{[l]}, y\right)}{\partial w_{j k}^{[l]}} ∂wjk[l]∂L(a[l],y) 和 ∂ L ( a [ l ] , y ) ∂ b j l \frac{\partial L\left(a^{[l]}, y\right)}{\partial b_{j}^{l}} ∂bjl∂L(a[l],y) 。
定义网络中第 l l l 层第 j j j 个神经元的误差为 δ j [ l ] \delta_{j}^{[l]} δj[l] :
δ j [ l ] = ∂ L ( a [ L ] , y ) ∂ z j [ l ] \delta_{j}^{[l]}=\frac{\partial L\left(a^{[L]},y\right)}{\partial z_{j}^{[l]}} δj[l]=∂zj[l]∂L(a[L],y)
其中 L ( a [ L ] , y ) L(a^{[L]},y) L(a[L],y) 表示损失函数, y y y 表示真实值, a [ L ] a^{[L]} a[L] 表示输出层的预测值。
每一层的误差向量可以表示为:
δ [ l ] = [ δ 1 [ l ] δ 2 [ l ] ⋮ δ n [ l ] ] \delta^{[l]}=\left[\begin{array}{c}\delta_{1}^{[l]} \\ \delta_{2}^{[l]} \\ \vdots \\ \delta_{n}^{[l]}\end{array}\right] δ[l]=⎣⎡δ1[l]δ2[l]⋮δn[l]⎦⎤
等式一 输出层误差
δ j [ L ] = ∂ L ∂ a j [ L ] σ ′ ( z j [ L ] ) \delta_{j}^{[L]}=\frac{\partial L}{\partial a_{j}^{[L]}} \sigma^{\prime}\left(z_{j}^{[L]}\right) δj[L]=∂aj[L]∂Lσ′(zj[L])
L表示输出层层数。以下用 ∂ L \partial L ∂L 表示 ∂ L ( a [ L ] , y ) \partial L\left(a^{[L]}, y\right) ∂L(a[L],y)
写成矩阵形式是:
δ [ L ] = [ ∂ L ∂ a 1 [ L ] ∂ L ∂ a 2 [ L ] ⋮ ∂ L ∂ a j [ L ] ] ⊙ [ σ ′ ( z 1 [ L ] ) σ ′ ( z 2 [ L ] ) ⋮ σ ′ ( z j [ L ] ) ] \delta^{[L]}= \left[\begin{array}{c}\frac{\partial L}{\partial a_{1}^{[L]}} \\ \frac{\partial L}{\partial a_{2}^{[L]}} \\ \vdots \\ \frac{\partial L}{\partial a_{j}^{[L]}}\end{array}\right] \odot\left[\begin{array}{c}\sigma^{\prime}\left(z_{1}^{[L]}\right) \\ \sigma^{\prime}\left(z_{2}^{[L]}\right) \\ \vdots \\ \sigma^{\prime}\left(z_{j}^{[L]}\right)\end{array}\right] δ[L]=⎣⎡∂a1[L]∂L∂a2[L]∂L⋮∂aj[L]∂L⎦⎤⊙⎣⎡σ′(z1[L])σ′(z2[L])⋮σ′(zj[L])⎦⎤
表示成公式:
δ [ L ] = ∇ a L ⊙ σ ′ ( z [ L ] ) \delta^{[L]}=\nabla_{a} L \odot \sigma^{\prime}\left(z^{[L]}\right) δ[L]=∇aL⊙σ′(z[L])
推导
计算输出层的误差 δ j [ L ] = ∂ L ∂ z j [ L ] \delta_{j}^{[L]}=\frac{\partial L}{\partial z_{j}^{[L]}} δj[L]=∂zj[L]∂L ,根据链式法则
δ j [ L ] = ∑ k ∂ L ∂ a k [ L ] ∂ a k [ L ] ∂ z j [ L ] \delta_{j}^{[L]}=\sum_{k} \frac{\partial L}{\partial a_{k}^{[L]}} \frac{\partial a_{k}^{[L]}}{\partial z_{j}^{[L]}} δj[L]=∑k∂ak[L]∂L∂zj[L]∂ak[L]
输出层不一定只有一个神经元,可能有多个神经元。成本函数是每个输出神经元的损失函数之和,每个输出神经元的误差与其它神经元没有关系,所以只有 k = j k=j k=j 的时候值不是0。
当 k ≠ j k\neq j k=j 时, ∂ L ∂ z j [ L ] = 0 \frac{\partial L}{\partial z_{j}^{[L]}}=0 ∂zj[L]∂L=0 ,简化误差 δ j [ L ] \delta_{j}^{[L]} δj[L] ,得到
δ j [ L ] = ∂ L ∂ a j [ L ] ∂ a j [ L ] ∂ z j [ L ] \delta_{j}^{[L]}=\frac{\partial L}{\partial a_{j}^{[L]}} \frac{\partial a_{j}^{[L]}}{\partial z_{j}^{[L]}} δj[L]=∂aj[L]∂L∂zj[L]∂aj[L]
σ \sigma σ 表示激活函数,由 a j [ L ] = σ ( z j [ L ] ) a_{j}^{[L]}=\sigma\left(z_{j}^{[L]}\right) aj[L]=σ(zj[L]),计算出 ∂ a j [ L ] ∂ z j [ L ] = σ ′ ( z j [ L ] ) \frac{\partial a_{j}^{[L]}}{\partial z_{j}^{[L]}}=\sigma^{\prime}\left(z_{j}^{[L]}\right) ∂zj[L]∂aj[L]=σ′(zj[L]) ,代入最后得到
δ j [ L ] = ∂ L ∂ a j [ L ] σ ′ ( z j [ L ] ) \delta_{j}^{[L]}=\frac{\partial L}{\partial a_{j}^{[L]}} \sigma^{\prime}\left(z_{j}^{[L]}\right) δj[L]=∂aj[L]∂Lσ′(zj[L])
等式二 隐藏层误差
δ j [ l ] = ∑ k w k j [ l + 1 ] δ k [ l + 1 ] σ ′ ( z j [ l ] ) \begin{array}{c} \delta_{j}^{[l]}=\sum_{k} w_{k j}^{[l+1]} \delta_{k}^{[l+1]} \sigma^{\prime}\left(z_{j}^{[l]}\right) \end{array} δj[l]=∑kwkj[l+1]δk[l+1]σ′(zj[l])
写成矩阵形式:
δ [ l ] = [ [ w 11 [ l ] w 12 [ l ] … w 1 k [ l ] w 21 [ l ] w 22 [ l ] … w 2 k [ l ] ⋮ ⋮ ⋱ ⋮ w j 1 [ l ] w j 2 [ l ] … w j k [ l ] ] [ δ 1 [ l + 1 ] δ 2 [ l + 1 ] ⋮ δ k [ l + 1 ] ] ] ⊙ [ σ ′ ( z 1 [ l ] ) σ ′ ( z 2 [ l ] ) ⋮ σ ′ ( z j [ l ] ) ] \delta^{[l]}=\left[\begin{array}{lll} \left[\begin{array}{lll}w_{11}^{[l]} & w_{12}^{[l]} & \dots & w_{1k}^{[l]} \\ w_{21}^{[l]} & w_{22}^{[l]} & \dots & w_{2k}^{[l]} \\ \vdots & \vdots & \ddots & \vdots\\ w_{j1}^{[l]} & w_{j2}^{[l]} & \dots & w_{jk}^{[l]} \end{array}\right] \left[\begin{array}{c}\delta_{1}^{[l+1]} \\ \delta_{2}^{[l+1]} \\ \vdots \\ \delta_{k}^{[l+1]}\end{array}\right] \end{array}\right] \odot\left[\begin{array}{c}\sigma^{\prime}\left(z_{1}^{[l]}\right) \\ \sigma^{\prime}\left(z_{2}^{[l]}\right) \\ \vdots \\\sigma^{\prime}\left(z_{j}^{[l]}\right)\end{array}\right] δ[l]=⎣⎡⎣⎡w11[l]w21[l]⋮wj1[l]w12[l]w22[l]⋮wj2[l]……⋱…w1k[l]w2k[l]⋮wjk[l]⎦⎤⎣⎡δ1[l+1]δ2[l+1]⋮δk[l+1]⎦⎤⎦⎤⊙⎣⎡σ′(z1[l])σ′(z2[l])⋮σ′(zj[l])⎦⎤
矩阵形状:(j,k) * (k,1) ⊙ \odot ⊙ (j,1) = (j,1)
权重矩阵的形状从(k,j)转置变成(j,k)。
表示成公式:
δ [ l ] = [ w [ l + 1 ] T δ [ l + 1 ] ] ⊙ σ ′ ( z [ l ] ) \delta^{[l]}=\left[w^{[l+1]^{T}} \delta^{[l+1]}\right] \odot \sigma^{\prime}\left(z^{[l]}\right) δ[l]=[w[l+1]Tδ[l+1]]⊙σ′(z[l])
推导
z k [ l + 1 ] = ∑ j w k j [ l + 1 ] a j [ l ] + b k [ l + 1 ] = ∑ j w k j [ l + 1 ] σ ( z j [ l ] ) + b k [ l + 1 ] z_{k}^{[l+1]}=\sum_{j} w_{k j}^{[l+1]} a_{j}^{[l]}+b_{k}^{[l+1]}=\sum_{j} w_{k j}^{[l+1]} \sigma\left(z_{j}^{[l]}\right)+b_{k}^{[l+1]} zk[l+1]=∑jwkj[l+1]aj[l]+bk[l+1]=∑jwkj[l+1]σ(zj[l])+bk[l+1]
对 z j [ l ] z_{j}^{[l]} zj[l] 求偏导
∂ z k [ l + 1 ] ∂ z j [ l ] = w k j [ l + 1 ] σ ′ ( z j [ l ] ) \frac{\partial z_{k}^{[l+1]}}{\partial z_{j}^{[l]}}=w_{k j}^{[l+1]} \sigma^{\prime}\left(z_{j}^{[l]}\right) ∂zj[l]∂zk[l+1]=wkj[l+1]σ′(zj[l])
根据链式法则
δ j [ l ] = ∂ L ∂ z j [ l ] = ∂ L ∂ z k [ l + 1 ] ∂ z k [ l + 1 ] ∂ z j [ l ] = ∑ k w k j [ l + 1 ] δ k [ l + 1 ] σ ′ ( z j [ l ] ) \delta_{j}^{[l]}=\frac{\partial L}{\partial z_{j}^{[l]}}=\frac{\partial L}{\partial z_{k}^{[l+1]}}\frac{\partial z_{k}^{[l+1]}}{\partial z_{j}^{[l]}}=\sum_{k} w_{k j}^{[l+1]} \delta_{k}^{[l+1]} \sigma^{\prime}\left(z_{j}^{[l]}\right) δj[l]=∂zj[l]∂L=∂zk[l+1]∂L∂zj[l]∂zk[l+1]=∑kwkj[l+1]δk[l+1]σ′(zj[l])
等式三 参数变化率
∂ L ∂ b j [ l ] = δ j [ l ] ∂ L ∂ w j k [ l ] = a k [ l − 1 ] δ j [ l ] \begin{array}{c} \frac{\partial L}{\partial b_{j}^{[l]}}=\delta_{j}^{[l]} \\ \frac{\partial L}{\partial w_{j k}^{[l]}}=a_{k}^{[l-1]} \delta_{j}^{[l]} \end{array} ∂bj[l]∂L=δj[l]∂wjk[l]∂L=ak[l−1]δj[l]
写成矩阵形式:
∂ L ∂ b [ l ] = [ δ 1 [ l ] δ 2 [ l ] ⋮ δ j [ l ] ] = δ [ l ] \frac{\partial L}{\partial b^{[l]}}=\left[\begin{array}{c}\delta_{1}^{[l]} \\ \delta_{2}^{[l]} \\ \vdots \\ \delta_{j}^{[l]}\end{array}\right]=\delta^{[l]} ∂b[l]∂L=⎣⎡δ1[l]δ2[l]⋮δj[l]⎦⎤=δ[l]
矩阵形状:(j,1)
∂ L ∂ w [ l ] = [ δ 1 [ l ] δ 2 [ l ] ⋮ δ j [ l ] ] [ a 1 [ l ] a 2 [ l ] … a k [ l ] ] \frac{\partial L}{\partial w^{[l]}}=\left[\begin{array}{c}\delta_{1}^{[l]} \\ \delta_{2}^{[l]} \\ \vdots \\ \delta_{j}^{[l]}\end{array}\right] \left[\begin{array}{c}a_{1}^{[l]} a_{2}^{[l]}\dots a_{k}^{[l]} \end{array}\right] ∂w[l]∂L=⎣⎡δ1[l]δ2[l]⋮δj[l]⎦⎤[a1[l]a2[l]…ak[l]]
矩阵形状:(j,1) * (1,k) = (j,k)
注意: ∂ L ∂ w [ l ] \frac{\partial L}{\partial w^{[l]}} ∂w[l]∂L 是一个dim ( δ [ l ] ) \left(\delta^{[l]}\right) (δ[l]) 行 dim ( a [ l − 1 ] ) \operatorname{dim}\left(a^{[l-1]}\right) dim(a[l−1]) 列的矩阵, 和 w [ l ] w^{[l]} w[l] 的维度一致 ;$ \frac{\partial L}{\partial b^{[l]}}$ 是一个维度为 dim ( δ [ l ] ) \operatorname{dim}\left(\delta^{[l]}\right) dim(δ[l]) 的列向量
表示成公式:
∂ L ∂ b [ l ] = δ [ l ] ∂ L ∂ w [ l ] = δ [ l ] a [ l − 1 ] T \begin{array}{c} \frac{\partial L}{\partial b^{[l]}}=\delta^{[l]} \\ \frac{\partial L}{\partial w^{[l]}}=\delta^{[l]} a^{[l-1] T} \end{array} ∂b[l]∂L=δ[l]∂w[l]∂L=δ[l]a[l−1]T
推导
z j [ l ] = ∑ k w j k [ l ] a k [ l − 1 ] + b k [ l ] z_{j}^{[l]}=\sum_{k} w_{j k}^{[l]} a_{k}^{[l-1]}+b_{k}^{[l]} zj[l]=∑kwjk[l]ak[l−1]+bk[l]
L 对 b j [ l ] b_{j}^{[l]} bj[l] 求偏导,根据链式法则得到
∂ L ∂ b j [ l ] = ∂ L ∂ z j [ l ] ∂ z j [ l ] b j [ l ] = ∂ L ∂ z j [ l ] ∗ 1 = δ j [ l ] \frac{\partial L}{\partial b_{j}^{[l]}}=\frac{\partial L}{\partial z_{j}^{[l]}} \frac{\partial z_{j}^{[l]}}{b_{j}^{[l]}}= \frac{\partial L}{\partial z_{j}^{[l]}} * 1 = \delta_{j}^{[l]} ∂bj[l]∂L=∂zj[l]∂Lbj[l]∂zj[l]=∂zj[l]∂L∗1=δj[l]
L 对 w j k [ l ] w_{j k}^{[l]} wjk[l] 求偏导,根据链式法则得到
∂ L ∂ w j k [ l ] = ∂ L ∂ z j [ l ] ∂ z j [ l ] w j k [ l ] = a k [ l − 1 ] δ j [ l ] \frac{\partial L}{\partial w_{j k}^{[l]}}=\frac{\partial L}{\partial z_{j}^{[l]}} \frac{\partial z_{j}^{[l]}}{w_{j k}^{[l]}}=a_{k}^{[l-1]} \delta_{j}^{[l]} ∂wjk[l]∂L=∂zj[l]∂Lwjk[l]∂zj[l]=ak[l−1]δj[l]
等式四 参数更新
根据梯度下降法原理,朝着梯度的反方向更新参数
b j [ l ] ← b j [ l ] − α ∂ L ∂ b j [ l ] w j k [ l ] ← w j k [ l ] − α ∂ L ∂ w j k [ l ] \begin{array}{c} b_{j}^{[l]} \leftarrow b_{j}^{[l]}-\alpha \frac{\partial L}{\partial b_{j}^{[l]}} \\ w_{j k}^{[l]} \leftarrow w_{j k}^{[l]}-\alpha \frac{\partial L}{\partial w_{j k}^{[l]}} \end{array} bj[l]←bj[l]−α∂bj[l]∂Lwjk[l]←wjk[l]−α∂wjk[l]∂L
写成矩阵形式:
b [ l ] ← b [ l ] − α ∂ L ∂ b [ l ] w [ l ] ← w [ l ] − α ∂ L ∂ w [ l ] \begin{array}{l} b^{[l]} \leftarrow b^{[l]}-\alpha \frac{\partial L}{\partial b^{[l]}} \\ w^{[l]} \leftarrow w^{[l]}-\alpha \frac{\partial L}{\partial w^{[l]}} \end{array} b[l]←b[l]−α∂b[l]∂Lw[l]←w[l]−α∂w[l]∂L
这里的 α \alpha α 指的是学习率。学习率决定了反向传播过程中梯度下降的步长。
反向传播图解
计算输出层误差
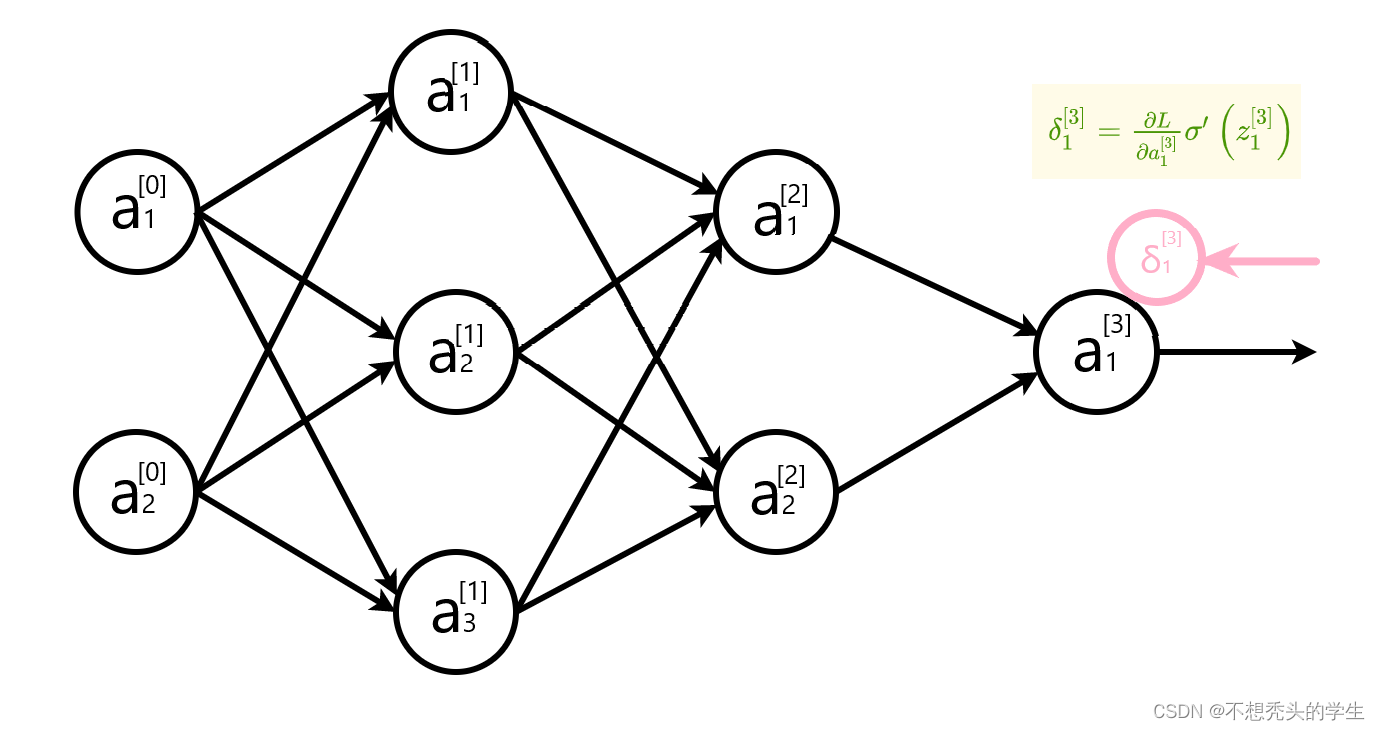
计算隐藏层误差

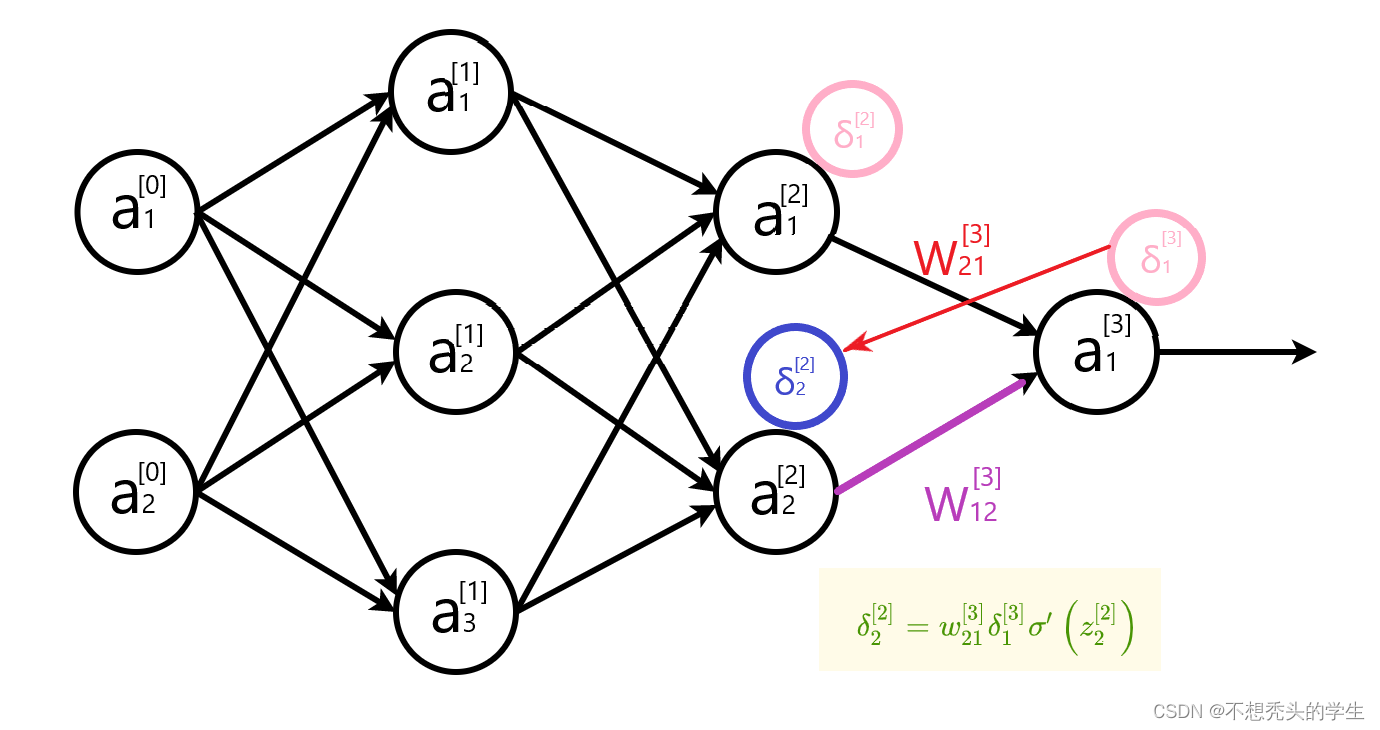
隐藏层误差公式写成矩阵形式 δ [ l ] = [ w [ l + 1 ] T δ [ l + 1 ] ] ⊙ σ ′ ( z [ l ] ) \delta^{[l]}=\left[w^{[l+1]^{T}} \delta^{[l+1]}\right] \odot \sigma^{\prime}\left(z^{[l]}\right) δ[l]=[w[l+1]Tδ[l+1]]⊙σ′(z[l]) 时, 权重矩阵需要转置。上面两幅图,直观地解释了转置的原因。
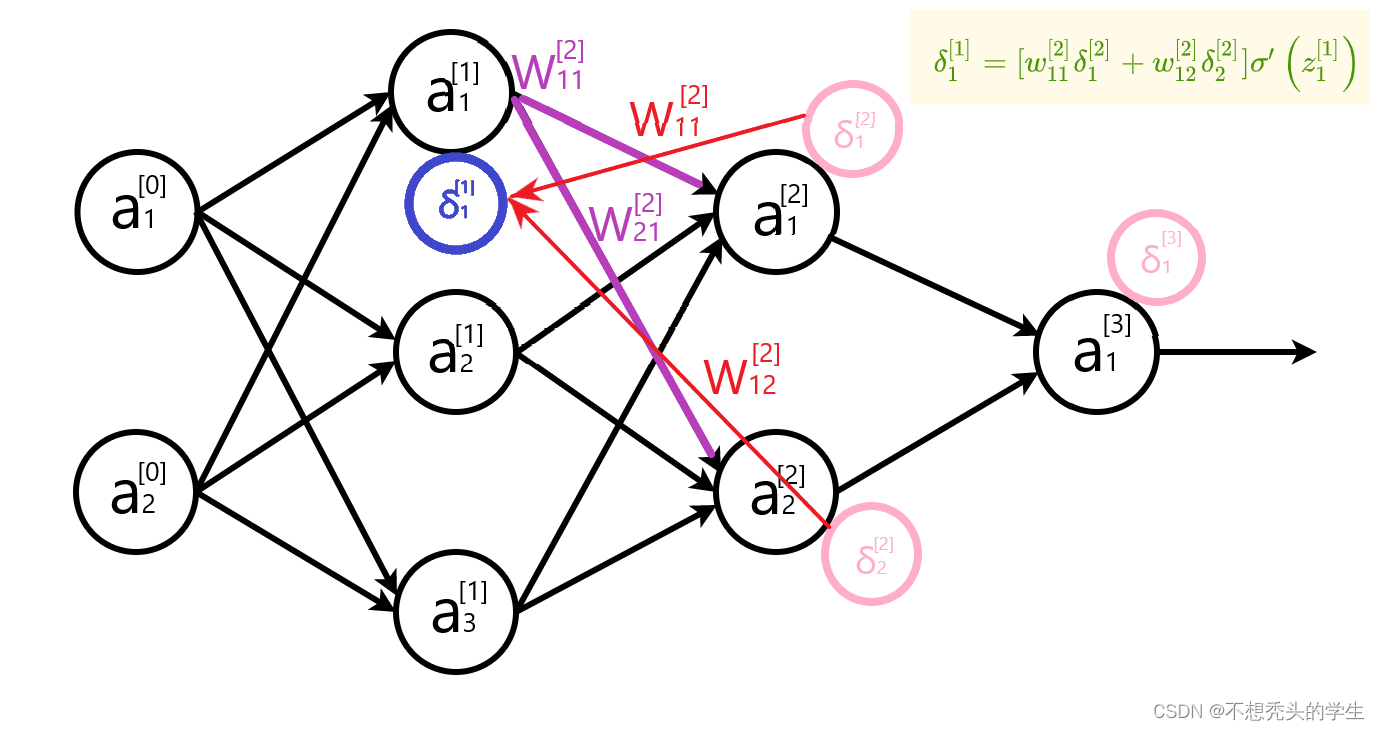


计算参数变化率

最后更新每层的参数。
反向传播公式总结
单样本输入公式表
| 说明 | 公式 |
|---|---|
| 输出层误差 | δ [ L ] = ∇ a L ⊙ σ ′ ( z [ L ] ) \delta^{[L]}=\nabla_{a} L \odot \sigma^{\prime}\left(z^{[L]}\right) δ[L]=∇aL⊙σ′(z[L]) |
| 隐含层误差 | δ [ l ] = [ w [ l + 1 ] T δ [ l + 1 ] ] ⊙ σ ′ ( z [ l ] ) \delta^{[l]}=\left[w^{[l+1]^{T}} \delta^{[l+1]}\right] \odot \sigma^{\prime}\left(z^{[l]}\right) δ[l]=[w[l+1]Tδ[l+1]]⊙σ′(z[l]) |
| 参数变化率 | ∂ L ∂ b [ l ] = δ [ l ] ∂ L ∂ w [ l ] = δ [ l ] a [ l − 1 ] T \begin{array}{c}\frac{\partial L}{\partial b^{[l]}}=\delta^{[l]} \\\frac{\partial L}{\partial w^{[l]}}=\delta^{[l]} a^{[l-1] T}\end{array} ∂b[l]∂L=δ[l]∂w[l]∂L=δ[l]a[l−1]T |
| 参数更新 | b [ l ] ← b [ l ] − α ∂ L ∂ b [ l ] w [ l ] ← w [ l ] − α ∂ L ∂ w [ l ] \begin{array}{l}b^{[l]} \leftarrow b^{[l]}-\alpha \frac{\partial L}{\partial b^{[l]}} \\w^{[l]} \leftarrow w^{[l]}-\alpha \frac{\partial L}{\partial w^{[l]}}\end{array} b[l]←b[l]−α∂b[l]∂Lw[l]←w[l]−α∂w[l]∂L |
多样本输入公式表
成本函数
多样本输入使用的成本函数与单样本不同。假设单样本的成本函数是交叉熵损失函数。
L ( a , y ) = − [ y ⋅ log ( a ) + ( 1 − y ) ⋅ log ( 1 − a ) ] L(a, y)=-[y \cdot \log (a)+(1-y) \cdot \log (1-a)] L(a,y)=−[y⋅log(a)+(1−y)⋅log(1−a)]
那么,对于m个样本输入,成本函数是每个样本的成本总和的平均值。
C ( A , y ) = − 1 m ∑ i = 0 m ( y ( i ) ⋅ log ( a ( i ) ) + ( 1 − y ( i ) ) ⋅ log ( 1 − a ( i ) ) ) C(A,y)=-\frac{1}{m} \sum_{i=0}^{m}\left(y^{(i)} \cdot \log \left(a^{(i)}\right)+\left(1-y^{(i)}\right) \cdot \log \left(1-a^{(i)}\right)\right) C(A,y)=−m1∑i=0m(y(i)⋅log(a(i))+(1−y(i))⋅log(1−a(i)))
误差
单样本输入的每一层的误差是一个列向量
δ [ l ] = [ δ 1 [ l ] δ 2 [ l ] ⋮ δ n [ l ] ] \delta^{[l]}=\left[\begin{array}{c}\delta_{1}^{[l]} \\ \delta_{2}^{[l]} \\ \vdots \\ \delta_{n}^{[l]}\end{array}\right] δ[l]=⎣⎡δ1[l]δ2[l]⋮δn[l]⎦⎤
而多样本输入的每一层的误差不再是一个列向量,变成一个m列的矩阵,每一列对应一个样本的向量。那么多样本的误差定义为:
d Z [ l ] = [ δ [ l ] ( 1 ) δ [ l ] ( 2 ) … δ [ l ] ( m ) ] = [ δ 1 [ l ] ( 1 ) δ 1 [ l ] ( 2 ) … δ 1 [ l ] ( m ) δ 2 [ l ] ( 1 ) δ 2 [ l ] ( 2 ) … δ 2 [ l ] ( m ) ⋮ ⋮ ⋱ ⋮ δ n [ l ] ( 1 ) δ n [ l ] ( 2 ) … δ n [ l ] ( m ) ] dZ^{[l]}=\left[\begin{array}{c}\delta^{[l](1)} \delta^{[l](2)} \dots \delta^{[l](m)}\end{array}\right]=\left[\begin{array}{c}\delta_{1}^{[l](1)}&\delta_{1}^{[l](2)}&\dots&\delta_{1}^{[l](m)} \\ \delta_{2}^{[l](1)}&\delta_{2}^{[l](2)}&\dots&\delta_{2}^{[l](m)} \\ \vdots & \vdots & \ddots & \vdots \\ \delta_{n}^{[l](1)}&\delta_{n}^{[l](2)}&\dots&\delta_{n}^{[l](m)} \end{array}\right] dZ[l]=[δ[l](1)δ[l](2)…δ[l](m)]=⎣⎡δ1[l](1)δ2[l](1)⋮δn[l](1)δ1[l](2)δ2[l](2)⋮δn[l](2)……⋱…δ1[l](m)δ2[l](m)⋮δn[l](m)⎦⎤
d Z [ l ] dZ^{[l]} dZ[l]的维度是 n × m n×m n×m , n n n 表示第 l l l 层神经元的个数, m m m 表示样本数量。
参数变换率
因为 d Z [ l ] dZ^{[l]} dZ[l]的维度是 j × m j×m j×m ,更新 b [ l ] b^{[l]} b[l] 的时候需要对每行求平均值,使得维度变为 j × 1 j×1 j×1,再乘以 1 m \frac{1}{m} m1。
d Z [ l ] dZ^{[l]} dZ[l]的维度是 j × m j×m j×m ,$A^{[l-1]T} $ 的维度是 m × k m×k m×k,矩阵相乘得到的维度是 j × k j×k j×k ,与 w [ l ] w^{[l]} w[l] 本身的维度相同。因此更新 w [ l ] w^{[l]} w[l] 时只需乘以 1 m \frac{1}{m} m1 求平均值。
| 说明 | 公式 |
|---|---|
| 输出层误差 | d Z [ L ] = ∇ A C ⊙ σ ′ ( Z [ L ] ) d Z^{[L]}=\nabla_{A} C \odot \sigma^{\prime}\left(Z^{[L]}\right) dZ[L]=∇AC⊙σ′(Z[L]) |
| 隐含层误差 | d Z [ l ] = [ w [ l + 1 ] T d Z [ l + 1 ] ] ⊙ σ ′ ( Z [ l ) ] d Z^{[l]}=\left[w^{[l+1] T} d Z^{[l+1]}\right] \odot \sigma^{\prime}\left(Z^{[l)}\right] dZ[l]=[w[l+1]TdZ[l+1]]⊙σ′(Z[l)] |
| 参数变化率 | d b [ l ] = ∂ C ∂ b [ l ] = 1 m m e a n O f E a c h R o w ( d Z [ l ] ) d w [ l ] = ∂ C ∂ w [ l ] = 1 m d Z [ l ] A [ l − 1 ] T d b^{[l]}=\frac{\partial C}{\partial b^{[l]}}=\frac{1}{m} m e a n O f E a c h R o w\left(d Z^{[l]}\right) \\d w^{[l]}=\frac{\partial C}{\partial w^{[l]}}=\frac{1}{m} d Z^{[l]} A^{[l-1] T} db[l]=∂b[l]∂C=m1meanOfEachRow(dZ[l])dw[l]=∂w[l]∂C=m1dZ[l]A[l−1]T |
| ------------: | |
| 输出层误差 | d Z [ L ] = ∇ A C ⊙ σ ′ ( Z [ L ] ) d Z^{[L]}=\nabla_{A} C \odot \sigma^{\prime}\left(Z^{[L]}\right) dZ[L]=∇AC⊙σ′(Z[L]) |
| 隐含层误差 | d Z [ l ] = [ w [ l + 1 ] T d Z [ l + 1 ] ] ⊙ σ ′ ( Z [ l ) ] d Z^{[l]}=\left[w^{[l+1] T} d Z^{[l+1]}\right] \odot \sigma^{\prime}\left(Z^{[l)}\right] dZ[l]=[w[l+1]TdZ[l+1]]⊙σ′(Z[l)] |
| 参数变化率 | d b [ l ] = ∂ C ∂ b [ l ] = 1 m m e a n O f E a c h R o w ( d Z [ l ] ) d w [ l ] = ∂ C ∂ w [ l ] = 1 m d Z [ l ] A [ l − 1 ] T d b^{[l]}=\frac{\partial C}{\partial b^{[l]}}=\frac{1}{m} m e a n O f E a c h R o w\left(d Z^{[l]}\right) \\d w^{[l]}=\frac{\partial C}{\partial w^{[l]}}=\frac{1}{m} d Z^{[l]} A^{[l-1] T} db[l]=∂b[l]∂C=m1meanOfEachRow(dZ[l])dw[l]=∂w[l]∂C=m1dZ[l]A[l−1]T |
| 参数更新 | b [ l ] ← b [ l ] − α ∂ C ∂ b [ l ] w [ l ] ← w [ l ] − α ∂ C ∂ w [ l ] \begin{array}{l}b^{[l]} \leftarrow b^{[l]}-\alpha \frac{\partial C}{\partial b^{[l]}} \\w^{[l]} \leftarrow w^{[l]}-\alpha \frac{\partial C}{\partial w^{[l]}}\end{array} b[l]←b[l]−α∂b[l]∂Cw[l]←w[l]−α∂w[l]∂C |
边栏推荐
猜你喜欢
随机推荐
第4讲:SQL语句之DDL类型的数据库定义语言
01. Preface
CS231n: 12 Reinforcement Learning
echart 股票数据分析 开发备忘录
Vue program of web cache problem after packaging
【761. Special binary sequence】
01、前言
Laravel 5.8笔记
FTP服务初探
Flush can buy stock?Is it safe to buy stocks?
荧光探针/近红外荧光/荧光纳米/水凝胶/纳米水凝胶pH荧光探针的研究
21天学习挑战赛——机器学习03
十六、一起学习Lua 文件 I/O
uva1432
连接工具和idea能查询出数据库数据,项目中查不到数据库数据:解决办法
LeetCode:每日一题【第二周】
feign的性能优化、Feign的使用-最佳优化两种方案
PX4模块设计之十八:Logger模块
torchvision.transforms
ABAP 报表中如何给报表的输入参数增添 F4 Value Help