当前位置:网站首页>Chinese Remainder Theorem and extended Chinese remainder theorem that can be understood by Aunt Baojie
Chinese Remainder Theorem and extended Chinese remainder theorem that can be understood by Aunt Baojie
2022-04-23 09:34:00 【Zimba_】
background :
This theorem is also called Sun Tzu theorem , The question was first raised in the northern and Southern Dynasties 《 Grandson The art of war Sutra 》 in ,“ I don't know the number of things , Two out of three , Three out of five , Two of the seven . Query geometry ?”,
namely , An integer divided by three and two , Divide by five and three , Divide by seven and two , Find this integer .
problem :
Solve Congruence Equations , Form like :( Piracy map , Weak awareness of copyright , What about a scholar? Can it be called stealing ?)
Before solving this problem , Let's be clear . Make M = l c m ( m 1 , m 2 , … , m n ) M=lcm(m_{1},m_{2},…,m_{n}) M=lcm(m1,m2,…,mn), If the equation has a solution , The answer must be x 0 + k M x_{0}+kM x0+kM In the form of , That is, the solution is in the module M Unique in the sense .
First x 0 x_{0} x0 Is a set of special solutions of the equation , Second, no matter which equation is substituted k M kM kM Will always be eliminated .
Chinese remainder theorem : Portal
First ask a simple version of the problem , That is, the of the equation Modulus is reciprocal .
This is it. Naked Sun Tzu's theorem .
Grandson's approach is : We just have to find a way to Construct a set of solutions Just fine .
So how to construct ?
This construction method is similar to ** Newton interpolation Lagrange interpolation ** similar ( Thanks to the high school math teacher ).
Thinking sequence 1 , 2 , 3 , π 1,2,3,\pi 1,2,3,π, Construct a general term formula , bring f ( 1 ) = 1 , f ( 2 ) = 2 , f ( 3 ) = 3 , f ( 4 ) = π f(1)=1,f(2)=2,f(3)=3,f(4)=\pi f(1)=1,f(2)=2,f(3)=3,f(4)=π.
The function is constructed by Lagrange interpolation :
f ( x ) = 1 × ( x − 2 ) ( x − 3 ) ( x − 4 ) ( 1 − 2 ) ( 1 − 3 ) ( 1 − 4 ) + f(x)=1 \times \frac{(x-2)(x-3)(x-4)}{(1-2)(1-3)(1-4)}+ f(x)=1×(1−2)(1−3)(1−4)(x−2)(x−3)(x−4)+ 2 × ( x − 1 ) ( x − 3 ) ( x − 4 ) ( 2 − 1 ) ( 2 − 3 ) ( 2 − 4 ) + 2 \times \frac{(x-1)(x-3)(x-4)}{(2-1)(2-3)(2-4)}+ 2×(2−1)(2−3)(2−4)(x−1)(x−3)(x−4)+ 3 × ( x − 1 ) ( x − 2 ) ( x − 4 ) ( 3 − 1 ) ( 3 − 2 ) ( 3 − 4 ) + 3 \times \frac{(x-1)(x-2)(x-4)}{(3-1)(3-2)(3-4)}+ 3×(3−1)(3−2)(3−4)(x−1)(x−2)(x−4)+ π × ( x − 1 ) ( x − 2 ) ( x − 3 ) ( 4 − 1 ) ( 4 − 2 ) ( 4 − 3 ) \pi \times \frac{(x-1)(x-2)(x-3)}{(4-1)(4-2)(4-3)} π×(4−1)(4−2)(4−3)(x−1)(x−2)(x−3)
This fairy principle is quite obvious , Each item consists of two parts , × \times × On the left is the number of each item , × \times × On the right is the control factor that determines whether an item exists , When x x x by 1 1 1 when , In addition to 1 1 1 The other three control factors are 0 0 0, And the first item is 1 1 1, That's the guarantee , Corresponding x x x We can get the corresponding item we want .
Then come back to our question , How to construct a set of solutions , Satisfy all the equations .
We make M = m 1 m 2 m 3 … m n M=m_{1}m_{2}m_{3}…m_{n} M=m1m2m3…mn.
Re order M i = M / m i M_{i}=M/m_{i} Mi=M/mi, It's our control factor .
Then we're going to start constructing special solutions x 0 x_{0} x0 了 .
According to the previous idea Angrily Just structure .
We first Violently Fill in each item in the formula .
x 0 = a 1 + a 2 + … + a n x_{0}=a_{1}\; \; \; \; \; \; \; \; \; \; \; \; +a_{2}\; \; \; \; \; \; \; \; \; \; \; \; +…+a_{n}\; \; \; \; \; \; \; \; \; \; \; \; x0=a1+a2+…+an
Then we put the control factor M i M_{i} Mi Fill in .
x 0 = a 1 M 1 + a 2 M 2 + … + a n M n x_{0}=a_{1}M_{1}\; \; \; \; \; \; \; +a_{2}M_{2}\; \; \; \; \; \; \; +…+a_{n}M_{n}\; \; \; \; \; \; \; x0=a1M1+a2M2+…+anMn
Now bring it to the i i i In two equations , except a i M i a_{i}M_{i} aiMi All other items will be eliminated , This is the only item left .
Then all we have to do is put M i M_{i} Mi And it's gone , only a i a_{i} ai, So we multiply it by its inverse , It becomes the last formula .
x 0 = a 1 M 1 M 1 − 1 + a 2 M 2 M 2 − 1 + … + a n M n M n − 1 x_{0}=a_{1}M_{1}M_{1}^{-1}+a_{2}M_{2}M_{2}^{-1}+…+a_{n}M_{n}M_{n}^{-1} x0=a1M1M1−1+a2M2M2−1+…+anMnMn−1
here M i − 1 M_{i}^{-1} Mi−1 Is the mould m i m_{i} mi In the sense of , What I have understood before , It should be known .
The last time I want to write the formula again :
x 0 ≡ a 1 M 1 M 1 − 1 + a 2 M 2 M 2 − 1 + … + a n M n M n − 1 ( m o d M ) x_{0}\equiv a_{1}M_{1}M_{1}^{-1}+a_{2}M_{2}M_{2}^{-1}+…+a_{n}M_{n}M_{n}^{-1}(mod\;M) x0≡a1M1M1−1+a2M2M2−1+…+anMnMn−1(modM)
also , Remember that the premise is to be mutually prime , Otherwise, there will be no inverse element in the step of finding the inverse element .
Templates :( correct , Fast multiplication is used to prevent overflow )
#include <bits/stdc++.h>
using namespace std;
typedef __int128 ll;
ll fmul(ll a,ll b,ll mod)
{
ll sum=0,base=(a%mod+mod)%mod;
while(b)
{
if(b%2)sum=(sum+base)%mod;
base=(base+base)%mod;
b/=2;
}
return sum;
}
ll read()
{
int X=0,w=0; char ch=0;
while(!isdigit(ch)) {
w|=ch=='-';ch=getchar();}
while(isdigit(ch)) X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
return w?-X:X;
}
void print(ll x)
{
if(x<0){
putchar('-');x=-x;}
if(x>9) print(x/10);
putchar(x%10+'0');
}
ll ex_gcd(ll a,ll b,ll& x,ll& y)
{
if(b==0)
{
x=1;y=0;
return a;
}
ll ans=ex_gcd(b,a%b,x,y);
ll tmp=x;
x=y;
y=tmp-a/b*y;
return ans;
}
ll inv(ll a,ll mod)// Existence of inverse element condition :gcd(a,mod)=1
{
ll x,y;
ll g=ex_gcd(a,mod,x,y);
if(g!=1)return -1;
return (x%mod+mod)%mod;
}
ll a[100005],m[100005];
ll crt(ll *a,ll *m,ll n)// The length is 0 To n-1
{
ll M=1;
for(int i=0;i<n;i++)M=M*m[i];
ll ans=0;
for(int i=0;i<n;i++)
{
ll MM=M/m[i];
ans=(ans+fmul(fmul(a[i],MM,M),inv(MM,m[i]),M))%M;
}
return ans;
}
int main()
{
ll n;
n=read();
for(int i=0;i<n;i++)
{
m[i]=read();a[i]=read();
}
print(crt(a,m,n));
return 0;
}
Expand the Chinese Remainder Theorem : Portal
Now we need to solve the upgraded version of the problem , That is to say There are no modules that are mutually prime Under the condition of .
Since it is extended , So draw inferences from one instance
This is a completely different approach from the previous one .
consider , In front of me i − 1 i-1 i−1 The general solution of the equation is c + k M c+kM c+kM( M M M Is the least common multiple of the previous modulus ) when , Let's join the first i i i An equation x ≡ a i ( m o d m i ) x\equiv a_{i}\;(mod\;m_{i}) x≡ai(modmi). M M M Will become the least common multiple after adding a new module , We ask for a new model M M M Solution in the sense of .
Let's bring the previous general solution into the new equation , obtain c + k M ≡ a i ( m o d m i ) c+kM\equiv a_{i}\;(mod\;m_{i}) c+kM≡ai(modmi), Deformed to k M ≡ a i − c ( m o d m i ) kM\equiv a_{i}-c\;(mod\;m_{i}) kM≡ai−c(modmi).
Note that you can't multiply both sides at this time M M M Inverse element ( Because this has been adjusted all afternoon bug), Because there is no guarantee that M M M There is an inverse element . We ask for a new k k k, Convert the equation into M k + m i y = a i − c Mk+m_{i}y=a_{i}-c Mk+miy=ai−c.
At this point, if the equation has no solution , Then the equations have no solution .
We solved k k k Value , Then add the second i i i New after two equations c c c It becomes c + k M c+kM c+kM, and M It becomes the least common multiple of the addition number .
We can set the initial solution as a module 1 1 1 In the sense of 0 0 0, Add the equations one by one .
Templates :
#include <bits/stdc++.h>
using namespace std;
typedef __int128 ll;
inline ll read()
{
ll X=0,w=0; char ch=0;
while(!isdigit(ch)) {
w|=ch=='-';ch=getchar();}
while(isdigit(ch)) X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
return w?-X:X;
}
inline void print(ll x)
{
if(x<0){
putchar('-');x=-x;}
if(x>9) print(x/10);
putchar(x%10+'0');
}
ll fmul(ll a,ll b,ll mod)
{
ll sum=0,base=(a%mod+mod)%mod;
while(b)
{
if(b%2)sum=(sum+base)%mod;
base=(base+base)%mod;
b/=2;
}
return sum;
}
ll gcd(ll a,ll b)
{
return b?gcd(b,a%b):a;
}
ll ex_gcd(ll a,ll b,ll& x,ll& y)
{
if(b==0)
{
x=1;y=0;
return a;
}
ll g=ex_gcd(b,a%b,x,y);
ll tmp=x;
x=y;
y=tmp-a/b*y;
return g;
}
ll a[100005],m[100005];
ll ex_crt(ll *a,ll *m,ll n)// The length is 0 To n-1
{
ll M=1,c=0;
for(int i=0;i<n;i++)
{
ll t=(a[i]%m[i]-c%m[i]+m[i])%m[i];
ll x,y;
ll g=ex_gcd(M,m[i],x,y);
if(t%g!=0)return -1;
ll tM=M;
M*=m[i]/gcd(M,m[i]);
x=fmul(t/g,(x%M+M)%M,M);
c=(c%M+fmul(x,tM,M)+M)%M;
}
return (c%M+M)%M;
}
int main()
{
ll n;
n=read();
for(int i=0;i<n;i++)
{
m[i]=read();a[i]=read();
}
print(ex_crt(a,m,n));
putchar('\n');
return 0;
}
版权声明
本文为[Zimba_]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204230621425804.html
边栏推荐
- [geek challenge 2019] havefun1
- SAP pi / PO function operation status monitoring and inspection
- Kernel PWN learning (3) -- ret2user & kernel ROP & qwb2018 core
- NPM installation yarn
- PHP笔记(一):开发环境配置
- 112. 路径总和
- Set the maximum width of the body, but why does the background color of the body cover the whole page?
- Get trustedinstaller permission
- Kettle experiment (III)
- MySQL of database -- Fundamentals
猜你喜欢

Distributed message oriented middleware framework selection - Digital Architecture Design (7)

Leetcode-199 - right view of binary tree
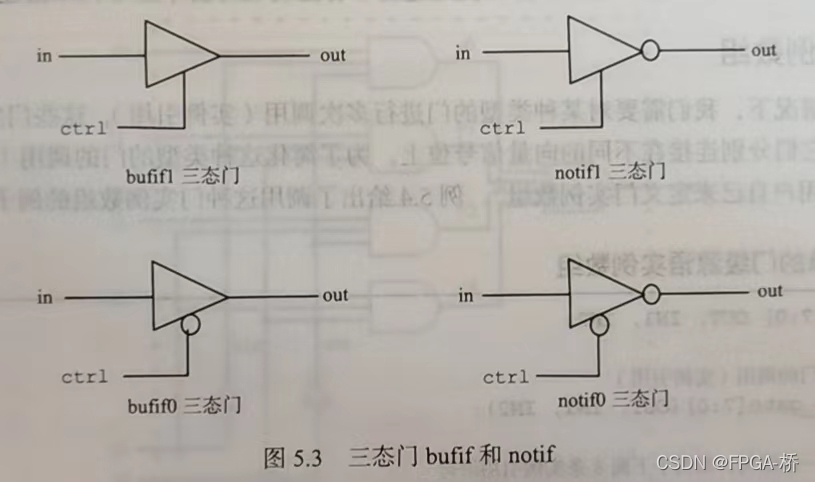
三、6【Verilog HDL】基础知识之门级建模

Flink 流批一体在小米的实践

【SQL server速成之路】数据库的视图和游标

Three challenges that a successful Devops leader should be aware of
![[SQL Server fast track] view and cursor of database](/img/2c/8edd92ecef11932c982db56af76c3f.png)
[SQL Server fast track] view and cursor of database

How to obtain geographical location based on photos and how to prevent photos from leaking geographical location
![[geek challenge 2019] havefun1](/img/8b/b15bf31771d54db25f24d630e64093.png)
[geek challenge 2019] havefun1

Pre parsing of JS
随机推荐
员工试用期转正申请书(泸州老窖)
Kettle实验 转换案例
Redis 异常 read error on connection 解决方案
JS scope, scope chain, global variables and local variables
Golang force buckle leetcode 396 Rotation function
MySQL of database -- overview and installation
Summary of wrong questions 1
Learn FPGA (from Verilog to HLS)
Go language learning notes - structure | go language from scratch
STM32 and FreeRTOS stack parsing
SAP 03-amdp CDs table function using 'with' clause
数据清洗 ETL 工具Kettle的安装
Cross domain configuration error: when allowcredentials is true, allowedorigins cannot contain the special value "*“
112. 路径总和
机器学习(六)——贝叶斯分类器
Number theory to find the sum of factors of a ^ B (A and B are 1e12 levels)
Two methods of building Yum source warehouse locally
Installation of data cleaning ETL tool kettle
Kettle experiment (III)
kettle庖丁解牛第14篇之JSON输入