当前位置:网站首页>2022牛客多校(七)K. Great Party博弈方法证明
2022牛客多校(七)K. Great Party博弈方法证明
2022-08-10 23:00:00 【abcpony】
又是一道博弈题目!对于我这种新手来说单证明个先手必赢策略就已经非常到力(潮汕话)!
链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
题目描述
Grammy joined a great party.
There is an interesting game at the party. There are nnn piles of stones on the table. The iii-th pile has aia_iai stones in it. Two players participate in the game and operate the stones in turn.
In each player's turn, the player will do the following two steps:
- Select a non-empty pile of stones, select a positive amount of stones to remove from it.
- Keep the remaining stones in the pile still or merge them all into another non-empty pile of stones.
Those who cannot operate lose the game.
Now, Grammy has qqq questions. For each question, she asks you how many sub-segments of [l,r][l,r][l,r] satisfy that if the piles in the segment are taken out alone for the game, the first player will win.
输入描述:
The first line contains two integers n,qn, qn,q (1≤n,q≤1051 \leq n, q \leq 10^51≤n,q≤105). The second line contains nnn integers a1,a2,…,ana_1,a_2,\ldots,a_na1,a2,…,an (1≤ai≤1061 \leq a_i \leq 10^61≤ai≤106). The iii-th of the next qqq lines contains two integers li,ril_i, r_ili,ri (1≤li≤ri≤n1 \leq l_i \leq r_i \leq n1≤li≤ri≤n).
输出描述:
The output contains qqq lines. Each line contains a single integer, denoting the answer to the question.
示例1
输入
4 5 1 2 2 4 1 2 2 3 3 4 1 3 2 4
输出
3 2 3 5 5
示例2
输入
4 5 5 6 7 8 1 2 2 3 3 4 1 3 2 4
输出
3 3 3 6 6
先手必胜策略:一个区间如果长度是奇数,那么先手必胜。否则如果石子个数减一的异或和不为0,先手必胜;否则后手必胜。
注意:下面的奇数控制偶数情况证明是不完全正确的(今天在别人题解下面献丑了)下面是我后来想的版本:对于奇数情况,首先把所有数字求异或和,然后取一个有S最高位上为1的数字A,和S异或得到B(明显B<A),再找一个B最高位m上对应为0的数字C(由于去掉A后偶数个数字的异或和为B,因此定有至少一个数字第m位为0),现让B和C两个数字从最低位(二进制)开始“计算”,由于我们要保证加了之后两个数字各个位置“1”的数量奇偶性不变,因此举个例子说明,1011(B)+0111(C),个位数当然是改变不了,就1+1->0,原本2个变成0依然为偶数可行,进一位遇到B、C两数都有1,原为2个“1”现在要3或者1,因此不行,就把B对应位上的1变成0(即1011->1001)此时此位依旧不变,2->0,再次进位,下一位中B为0而C为1即有一个,加了一个变成两个,那么就要把B此位再加上一个变为3个,再进位把3变成1个,直到目前为止前面的低位都是可以保持奇偶性的,现在来到了最高位,注意最高位有个特点,必然是一个为1一个为0,因此目前进了一个变2那么只需要把B该位上的1去掉即可,依然保持1个,若是最高位的运算中没有来进位,即B不用再改变,而进位最大也就是1了,由此,B“+”C得到的数字即可保证剩下的偶数个数字异或和为0!其他的就好证了。//至于为什么维护的是-1异或和为0,比如1,1,2,4,4其实它们的异或和已经是0了,因此根据理论无法进行其他操作,若是-1了的则不用再操作可行。
证明过程:(不完全正确((可以将先将1~n-1的数字异或求和得到S,取到数组中的最大值A,假设S的最高位k不是A的最高位,那么先找到一个k位不是1的数字B(由于是偶数个数字的异或和,则S为1处说明数字中至少有个此处为0的),再把A取到一个够小的情况A',使得A'+B后得到的数字能保证k位为1,并且低于k的位上数字能控制好奇偶性,从而能使得所有数字异或和为0;假设S的最高位就是A的最高位,那么可以找一个S第二高位m对应为1的某个数字C,能够控制将A取到一个数字A",有A"+C得到的数字k位上为1,而m位上为0,并且低于m的位置上控制好奇偶性使得异或和为0,比如上面例子1^1^1^4得到101,其中k位即A=5的最高位,那么找一个m位(最低位)上为1的数字1,然后在5上取掉1再加上1则为5,等于S,可得异或和为0。)))
上面所说例子中,若是1,1,4,4,1则A=4不再取,因此我们所说的是减一异或和,就当我上面的例子实际上是指2,2,5,6,2即可,对于下面的例子也是可行的,就算是就把它当例子也可行,毕竟上面已经有了证明。
补充:而对于遇到偶数且减一异或和P不0的情况,则可以找出对应P最高位上有1的数字,取到让它这个1没了,并低于这个位的01串能保证异或和为0(说的都是减了一的情况了)。
然而对于被我们控制的对方,他如果改变堆数为奇数那么沿用上面的方法,如果他不改变堆数而是在某个>1的堆上面取几个,首先将其他没被取的石子减一异或和求出,其结果等于被取堆没被取之前的数量,那么只要取了,到时候异或和肯定就又不为零了,那么又可以用上面证明的偶数取法了。
假设在某个偶数堆情况之后对方就一直不减小堆数量,我方当然也是保持偶数,那么随着每堆石头数量的减少必将到达偶数个1的情况,而次时减一异或和为0,即为对方先取,一个个取完当然就是我方胜利。假设对方没有维持某个偶数堆的情况,即堆数一直减少,而奇数在我这边,那最后一堆还是我取了,也是我方胜利!由此证毕。
边栏推荐
猜你喜欢
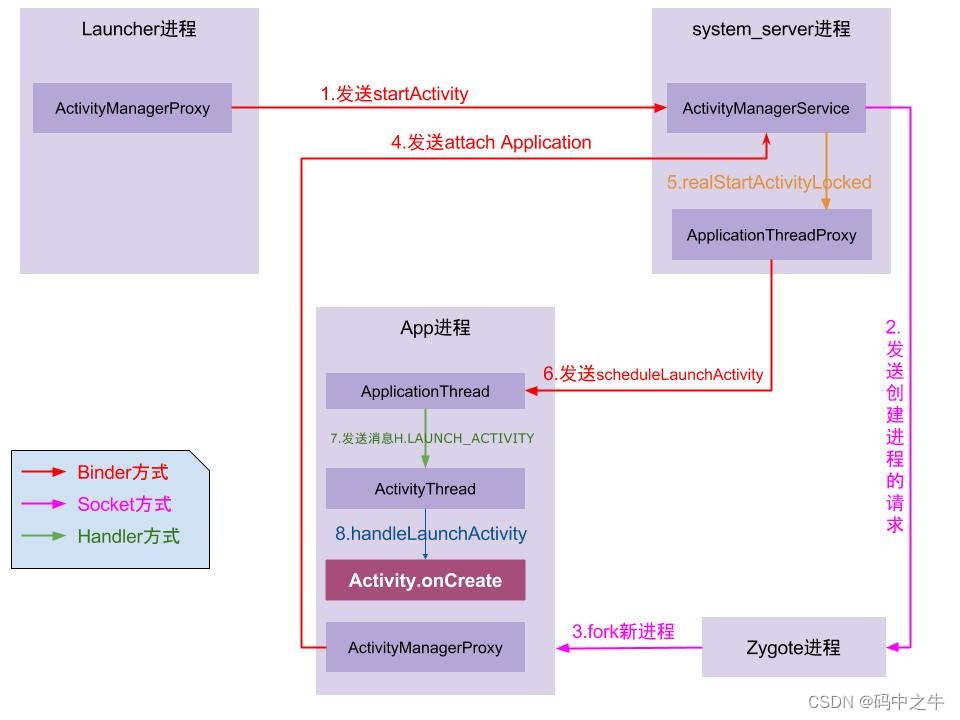
面试官: AMS在Android起到什么作用,简单的分析下Android的源码
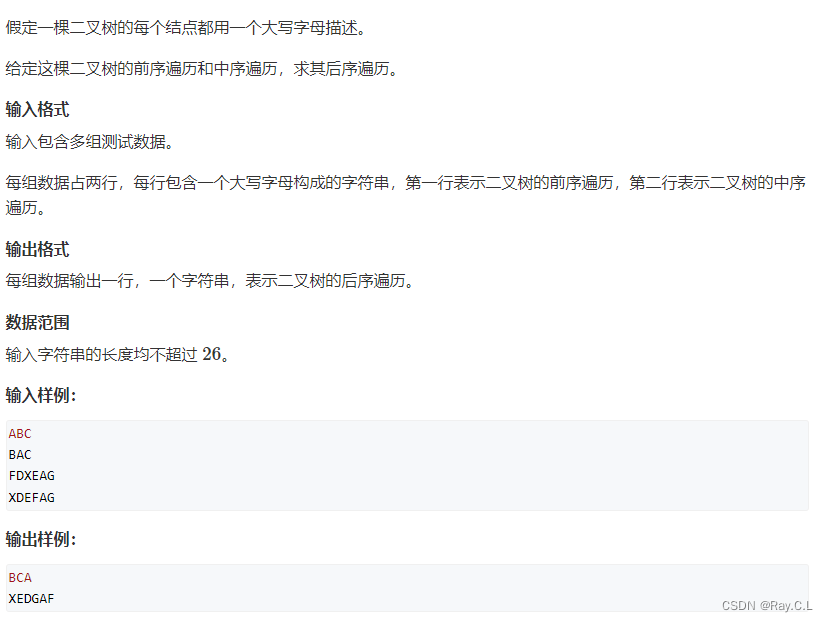
3598. Binary tree traversal (Huazhong University of Science and Technology exam questions)

JS学习 2022080
2021 IDEA creates web projects
二叉树 | 迭代遍历 | leecode刷题笔记

PyQt5 窗口自适应大小

大厂面试热点:“热修复机制及常见的几个框架介绍”
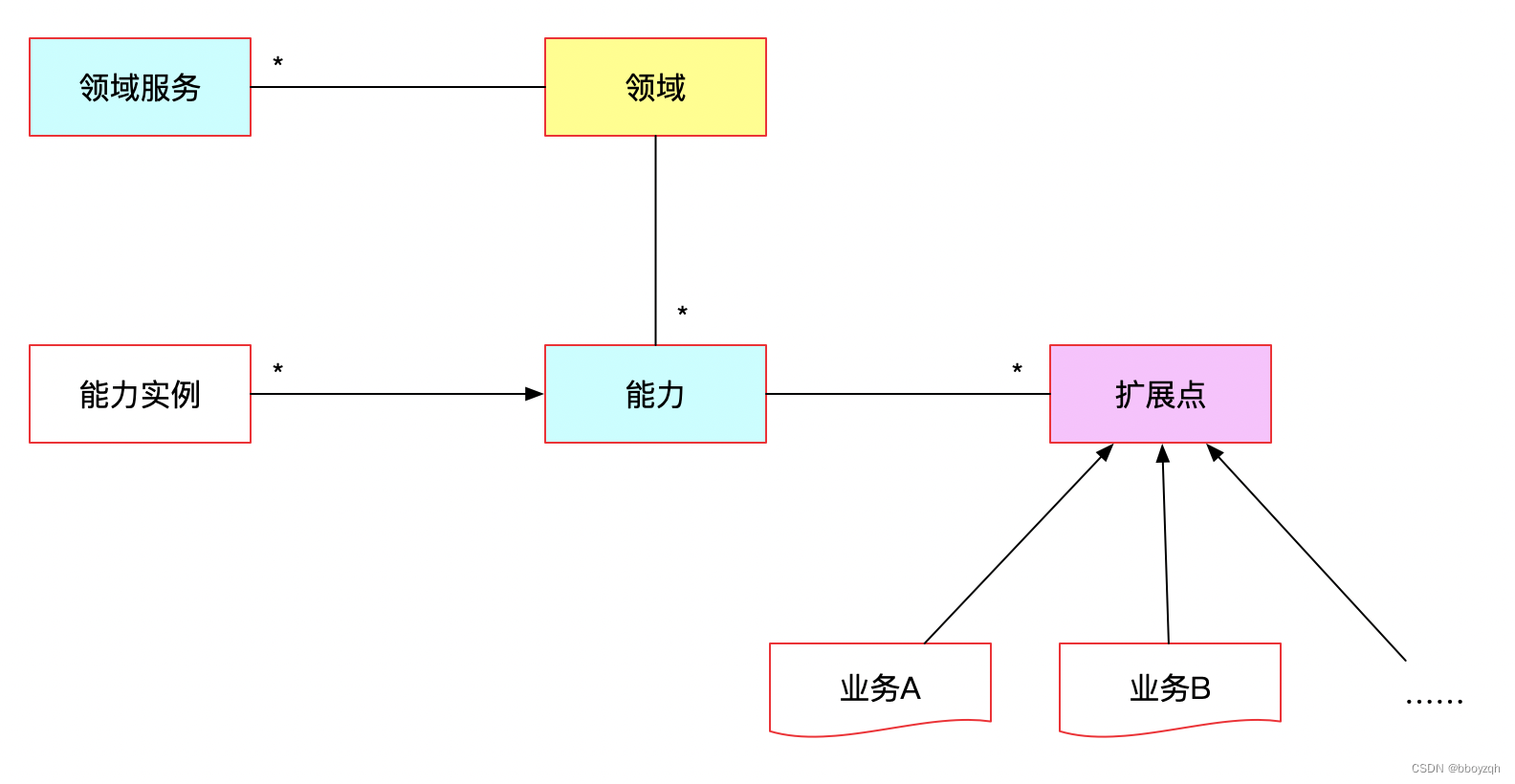
常用代码扩展点设计方式

Introduction to the use of counter instructions in Rockwell AB PLC RSLogix5000
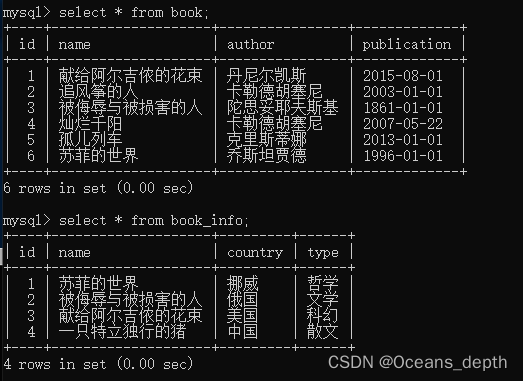
MySQL学习笔记(2)——简单操作
随机推荐
Pytorch面试题面经
一文带你了解 ViewModel 的使用及源码解析
怎么关闭电脑广告
MySQL之JDBC编程增删改查
Pengcheng Cup 2022 web/misc writeup
房间虚拟样板间vr制作及价格
RecyclerView设置缓存大小
细谈APP开发焦点问题:AMS 系统时间调节原理
实例051:按位与
PlaidCTF 2022 Amongst Ourselves:Shipmate writeup
Android面试冲刺:2022全新面试题——剑指Offer(备战金九银十)
N1BOOK writeup
高精度减法
二叉树 | 层序遍历 | leecode刷题笔记
EL表达式
(PC+WAP)带手机端pbootcms模板园林景观类网站
生态伙伴开发实践 | 智慧检测实验室应用系统快速接入指令集数字底座
分享一个后台管理系统可拖拽式组件的设计思路
二叉树 | 翻转二叉树 | leecode刷题笔记
HGAME 2022 Week3 writeup