Nioke 2022 Summer Multi-School 6 B Eezie and Pie (Difference on the tree + multiplication to find the kth ancestor board)

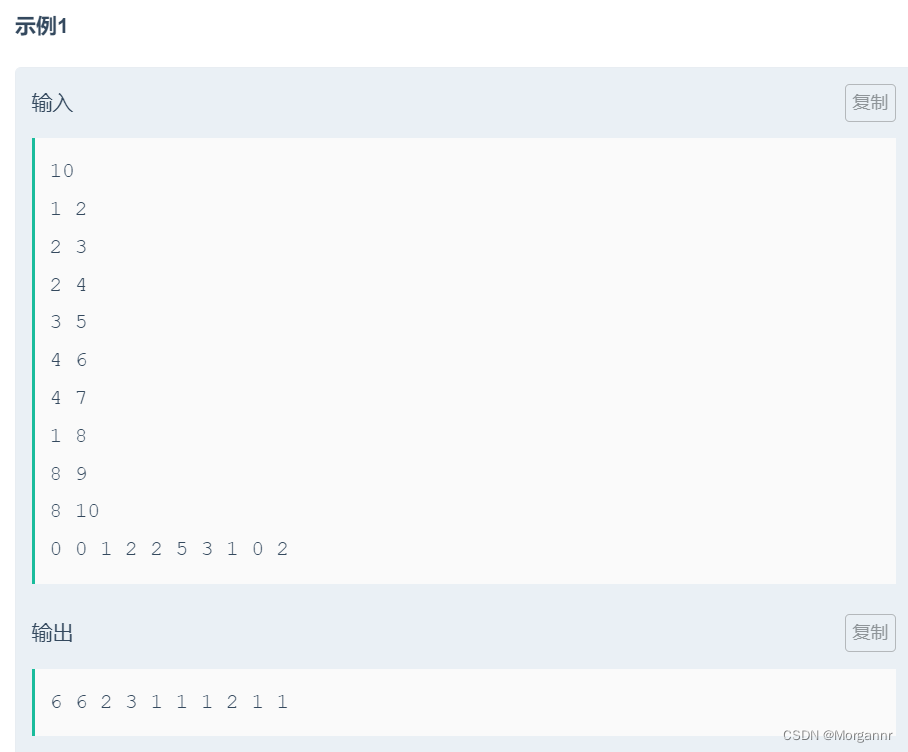
题意：

给定一棵树,要求输出 以 u 为 in the root subtree,How many node weights are satisfied 大于等于 其到 根节点 u 的 距离,u ∈ 1 ~ n.

思路：

以一棵 根节点为 u 的子树 为例子,我们从 贡献 from the perspective of analyzing the problem.

对于 子树中的某个节点（任意节点,包括 根）,我们分析一下 its contribution to the root node.（贡献 指的是 The number of nodes that satisfy the condition）

• 首先,Any node will Make it its own contribution plus 1.
• 其次,假设 节点权值为 w[u],它会使得 Its path towards the root node u ~ v（路径长度为 w[u]）上 所有节点 contributions 加上一个 1.

举个例子,Take the example in the question as an example：节点 6 的权值为 3,Then it will make 6 -> 4 -> 2 -> 1 All points on this path contribute plus 1.

The first thing I thought was 树链剖分,因为 树链剖分 可以 Converts a certain path in the tree to logn 段连续区间,进而用 线段树 进行 区间修改操作,但是由于其 时间复杂度是 O(n(logn)^2) 级别,题设 范围是 2e6,Obviously not allowed.

Then what algorithm can be Modify a path in the tree 呢,We can think of a more elegant approach,树上差分.

之前有提到过 一维数组的差分,可以 用 O(1) The time complexity of completing the operation of adding a certain number to a range,树上差分 也是类似.

具体做法：

• Differential markers on the tree,我们 在 dfs 的过程中完成.
• 当向下 Find a node u 时,我们 令 k 等于 其权值 w[u],前文已经提及,我们 目的是要将 u ~ v This length is k path as a whole + 1,那么转化为 差分操作,就是 在 u 节点 mark[u] ++,在 v 的父节点 mark[fa[v][0]] --（其中,v 为 u 的 第 k 个祖先：v = get_fa(u, w[u])）,即可完成.
  （此处类比 一维数组差分 帮助理解：在 区间 i ~ j 上加上 a,就应当 Make difference array c[i] += a,c[j + 1] -= a ）

void dfs(int u, int father) {
    
    int v = get_fa(u, w[u]);
    mark[u]++, mark[fa[v][0]]--;

    for (int i = h[u]; ~i; i = ne[i]) {
    
        int j = e[i];
        if (j == father) continue;
        dfs(j, u);
    }
}

• 如何求 u 的 第 k 个祖先 v ,如果暴力的话,显然是会 超时 的,要 倍增 look for（The following board is very important,用于 Find exponentially 节点 x 的 第 kth 祖先）.

int get_fa(int x, int k) {
    
	for (int i = 21; i >= 0; --i)
	{
    
	    if (k >= (1 << i))	//如果 k If this condition is met, keep jumping,until you reach your destination
	    {
    
	        k -= (1 << i);
	        x = fa[x][i];
	    }
	}
	return x;
}

• 之后进行 第二遍 dfs1,用于 Merge the difference array of all nodes bottom-up mark[u],类比 Convert a 1D difference array for 一遍 前缀和 求 原数组.至此,我们就完成了 Modification operations on paths in the tree.

void dfs1(int u, int father) {
    
    for (int i = h[u]; ~i; i = ne[i]) {
    
        int j = e[i];
        if (j == father) continue;
        dfs1(j, u);
        mark[u] += mark[j];
    }
}

时间复杂度：

$O(nlogn)$

代码：

#include <bits/stdc++.h>

using namespace std;
//#define map unordered_map
#define int long long
const int N = 2e6 + 10, M = N << 1;
int n;
int h[N], e[M], ne[M], w[N], idx;
int fa[N][22];
int depth[N];
int mark[N];

void add(int a, int b) {
    
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void bfs(int root)
{
    
    queue<int> q; q.push(root);
    while (q.size())
    {
    
        auto t = q.front(); q.pop();
        for (int i = h[t]; ~i; i = ne[i])
        {
    
            int j = e[i];
            if (depth[j] > depth[t] + 1)
            {
    
                depth[j] = depth[t] + 1;
                fa[j][0] = t;
                for (int k = 1; k <= 21; ++k)
                {
    
                    fa[j][k] = fa[fa[j][k - 1]][k - 1];
                }
                q.push(j);
            }
        }
    }
}

void init(int root)	//Classic pair fa Array preprocessing operations
{
    
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0, depth[root] = 1;
    bfs(root);
}

int get_fa(int x, int k) {
    
    for (int i = 21; i >= 0; --i)
    {
    
        if (k >= (1 << i))
        {
    
            k -= (1 << i);
            x = fa[x][i];
        }
    }
    return x;
}

void dfs(int u, int father) {
    
    int v = get_fa(u, w[u]);
    mark[u]++, mark[fa[v][0]]--;

    for (int i = h[u]; ~i; i = ne[i]) {
    
        int j = e[i];
        if (j == father) continue;
        dfs(j, u);
    }
}

void dfs1(int u, int father) {
    
    for (int i = h[u]; ~i; i = ne[i]) {
    
        int j = e[i];
        if (j == father) continue;
        dfs1(j, u);
        mark[u] += mark[j];
    }
}

signed main()
{
    
    memset(h, -1, sizeof h);
    cin >> n;
    int t = n - 1;
    while (t--)
    {
    
        int u, v; scanf("%lld%lld", &u, &v);
        add(u, v), add(v, u);
    }
    for (int i = 1; i <= n; ++i) {
    
        scanf("%lld", &w[i]);
    }
    init(1);
    dfs(1, -1);
    dfs1(1, -1);
    for (int i = 1; i <= n; ++i) {
    
        printf("%lld ", mark[i]);
    }

    return 0;
}