当前位置:网站首页>Implement general-purpose, high-performance sorting and quicksort optimizations
Implement general-purpose, high-performance sorting and quicksort optimizations
2022-08-11 07:14:00 【Eating too much sugar will not gain weight】
选择通用的、high performance sorting
| 时间复杂度 | 是否稳定排序 | 是否原地排序 | |
|---|---|---|---|
| 冒泡排序 | o(n2) | 是 | 是 |
| 插入排序 | o(n2) | 是 | 是 |
| 选择排序 | o(n2) | 否 | 是 |
| 快速排序 | o(nlogn) | 否 | 是 |
| 归并排序 | o(nlogn) | 是 | 否 |
| 计数排序 | o(n+k) k是数据范围 | 是 | 否 |
| 桶排序 | o(n) | 是 | 否 |
| 基数排序 | o(n) | 是 | 否 |
如何选择合适的排序算法
1.The time complexity of linear sorting is relatively low,But the use case is rather special,Therefore, when you want to choose a general sorting algorithm, you cannot choose linear sorting.
2.If it is a small-scale sorting,可以采用O(n2) 的算法,用时间换取空间;If it is a large-scale algorithm,通常采用O(nlogn)algorithm is efficient,用空间换取时间.Therefore, it is generally in order to take into account the sorting of data size,Generally, the time complexity is o(nlogn)的排序算法进行排序.
3.O(nlogn)The sorting algorithm is usually quicksort、归并排序、以及堆排序.In general, merge sort is not used much,Even worst case quicksort time complexity iso(n2),And just mergeo(nlogn),But the use of quicksort is still the most.This is because merge sort is not an in-place sort,空间复杂度是O(n),Merge sort calculation100M的数据,往往还需要100Mspace for the sorting algorithm to use,空间翻倍.when the data size is large,这个是很恐怖的.
优化快排
The worst case for quicksort is O(n2) ,即在最坏的情况下,The data is ordered or near ordered,The partition point is set on the last data,This is the worst.So the ideal partition point is The amount of data on the left and right sides of the partition point is similar.This will average out.
How to find the middle partition point.
三数取中法
从区间的首、中、Compare the last three numbers,Take the middle of the three numbers as the partition point.
代码:
/** Take the middle value of the first, middle and last,and move it to the end of the array. */
private static void midThree(int[] a, int start, int end) {
int mid = (start + end) / 2;
int min = Math.min(Math.min(a[start], a[mid]), a[end]);
int max = Math.max(Math.max(a[start], a[mid]), a[end]);
if (a[start] != min && a[start] != max) {
swap(a,start,end); //如果start 是中间值,移动到尾部
}else if (a[mid] != min && a[mid] != max){
swap(a,mid,end); //如果mid是中间值,移动到尾部
}
}
private static void swap(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
完整代码:
public static int quickPartition(int[] arr, int begin, int end){
int keyi = begin; // Set the leftmost point of the array as the partition point
while (begin < end){
// The left and right pointers are convenient
while (arr[end] >= arr[keyi] && begin < end){
--end;} //Find the number that the right pointer is smaller than the partition point
while (arr[begin] <= arr[keyi] && begin < end){
++begin;} //Find the number by which the left pointer is greater than the partition point
int tmp = arr[end]; // 交换数据
arr[end] = arr[begin];
arr[begin] = tmp;
}
int temp = arr[end]; //左右指针相遇,Move the partition point to the meeting point
arr[end] = arr[keyi];
arr[keyi] = temp;
keyi = end; //Find the latest partition point
return keyi;
}
public static void quickfindLarge1(int[] arr, int begin, int end){
if (begin >= end){
return;
}
//midThree(arr,begin,end);
int q = quickPartition(arr,begin,end);
quickfindLarge1(arr,begin,q-1);
quickfindLarge1(arr,q+1,end);
}
public static void quickfindLarge2(int[] arr, int begin, int end){
if (begin >= end){
return;
}
midThree(arr,begin,end);
int q = quickPartition(arr,begin,end);
quickfindLarge2(arr,begin,q-1);
quickfindLarge2(arr,q+1,end);
}
/** Take the middle value of the first, middle and last,and move it to the end of the array. */
private static void midThree(int[] a, int start, int end) {
int mid = (start + end) / 2;
int min = Math.min(Math.min(a[start], a[mid]), a[end]);
int max = Math.max(Math.max(a[start], a[mid]), a[end]);
if (a[start] != min && a[start] != max) {
swap(a,start,end); //如果start 是中间值,移动到尾部
}else if (a[mid] != min && a[mid] != max){
swap(a,mid,end); //如果mid是中间值,移动到尾部
}
}
private static void swap(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
结果比较:
随机数法
Take random numbers as partition points,There is no guarantee that each partition click is the best,But not the worst.No code is written here;
总结,General sorting implementation tips
1.数据量不大的时候,Adopt a time-for-space strategy,即冒泡、插入、选择
2.数据量大的时候,采用空间换时间,例如快排、基数等.
3.手动模拟栈(Prevent stack overflow caused by recursion)
4.Use Sentinel to optimize your code,Each sorting reduces judgment
5.Arrays.sort():
1.If the total number of array elements is less than 47,使用插入排序
2.If the total number of data elements is 47~286之间,使用快速排序.Should be the optimized version of the three-valued optimized version used.
3.若大于286的个数,使用归并排序.
边栏推荐
猜你喜欢
抖音API接口
会议OA项目之我的会议
八股文之mysql

Spatial Pyramid Pooling -Spatial Pyramid Pooling (including source code)
arcgis填坑_1
![[损失函数]——均方差](/img/55/e3c1797d5e87ddfb72bf39c5d31168.png)
[损失函数]——均方差

unable to extend table xxx by 1024 in tablespace xxxx
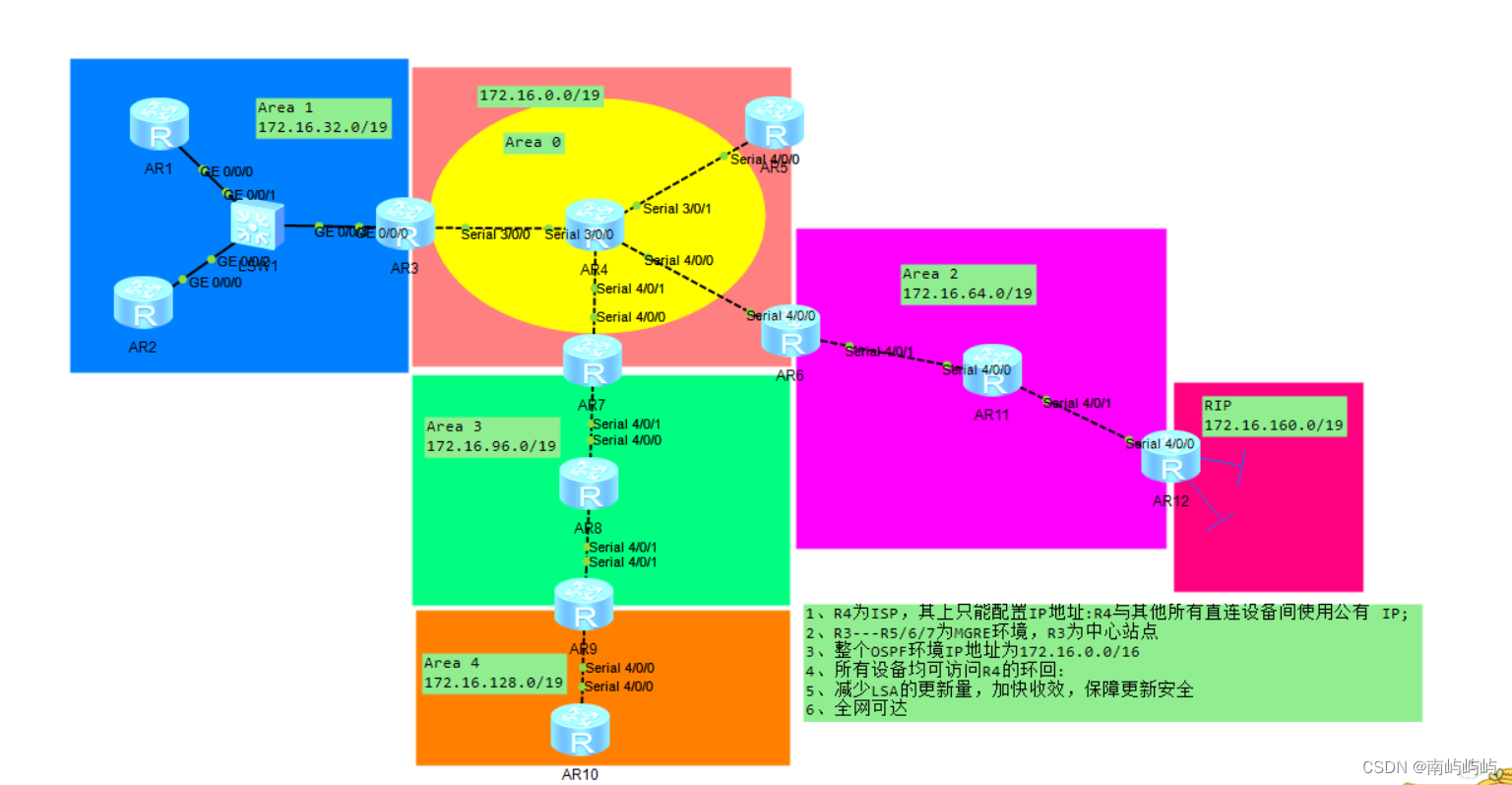
HCIP OSPF/MGRE Comprehensive Experiment
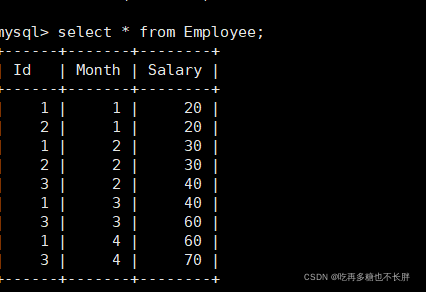
每日sql--统计员工近三个月的总薪水(不包括最新一个月)
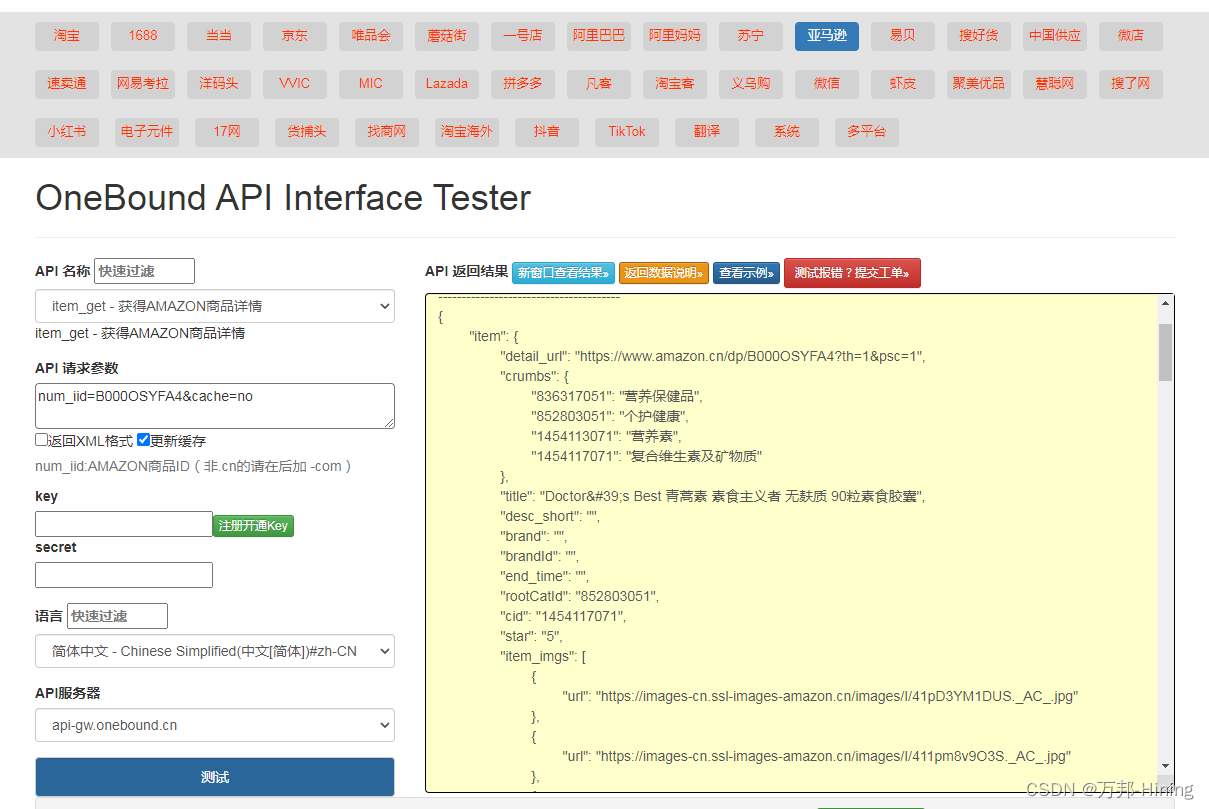
Amazon Get AMAZON Product Details API Return Value Description
随机推荐
京东商品详情API调用实例讲解
亚马逊API接口大全
拼多多API接口(附上我的可用API)
HCIP BGP neighbor building, federation, and aggregation experiments
华为防火墙-1-安全区域
HCIP-Spanning Tree (802.1D, Standard Spanning Tree/802.1W: RSTP Rapid Spanning Tree/802.1S: MST Multiple Spanning Tree)
arcgis填坑_2
iptables 流量统计
Class definition, class inheritance, and the use of super
WiFi Deauth 攻击演示分析 // mdk4 // aireplay-ng// Kali // wireshark //
抖音API接口
Spatial Pyramid Pooling -Spatial Pyramid Pooling (including source code)
grep、sed、awk
华为防火墙-4-安全策略
iptables nat
mmdetection的安装和训练、测试didi数据集的步骤(含结果)
导航定位中的坐标系
HCIP Republish/Routing Policy Experiment
numpy和tensor增加或删除一个维度
HCIP--交换基础