当前位置:网站首页>棋盘覆盖问题(分治)
棋盘覆盖问题(分治)
2022-04-22 05:37:00 【atwdy】
问题描述:在一个 2 k ∗ 2 k ( k > 0 ) 2^k*2^k(k>0) 2k∗2k(k>0)的棋盘,只有一个与其它方格不同的特殊方格,现在要用下图所示的 L 形骨牌覆盖除了特殊方格外的其它全部方格,任意两骨牌不能重叠,给出一种覆盖方法。

本题可以将大棋盘划分为四个大小相同的象限,那么这个特殊方格必定存在其中一个象限,根据方格存在的不同象限,L 形骨牌的摆法:

这样便能使被划分的四个象限均存在一个“特殊的方格”,达到分治的条件。
分治一个最重要的特点在于一个复杂的大问题可以分解为几个性质或求解思路相同的小问题,且小问题更容易求解。
代码实现过程中需要创建一个和初始棋盘大小相同的二维数组用来保存棋盘每个方格覆盖骨牌的编号。
java代码
public class Solution {
int tile; // 骨牌编号,从1开始
int[][] board; // 与初始棋盘对应的二维数组
public Solution(int size) {
// 构造函数,初始化
board = new int[size][size];
tile = 1;
}
// (tr,tc)表示一个象限左上角方格的行列号,(dr,dc)表示特殊方格行列号,其中初始棋盘左上角行列号(0,0)
public void chessBoard(int tr, int tc, int dr, int dc, int size) {
if (size == 1) {
// 递归出口
return;
}
int t = tile++; // 取骨牌
int s = size >> 1; // 分割棋盘
// 考虑左上角象限
if (dr < tr + s && dc < tc + s) {
// 特殊方格在此象限处理此象限
chessBoard(tr, tc, dr, dc, s);
} else {
// 特殊方格不在此象限
board[tr + s - 1][tc + s - 1] = t; // t号骨牌覆盖象限最右下角
chessBoard(tr, tc, tr + s - 1, tc + s - 1, s); // 将右下角视为特殊方格继续处理该象限
}
// 考虑右上角象限
if (dr < tr + s && dc >= tc + s) {
// 特殊方格在此象限处理此象限
chessBoard(tr, tc + s, dr, dc, s);
} else {
// 特殊方格不在此象限
board[tr + s - 1][tc + s] = t; // t号骨牌覆盖象限最左下角
chessBoard(tr, tc + s, tr + s - 1, tc + s, s); // 将左下角视为特殊方格继续处理该象限
}
// 考虑左下角象限
if (dr >= tr + s && dc < tc + s) {
// 特殊方格在此象限处理此象限
chessBoard(tr + s, tc, dr, dc, s);
} else {
// 特殊方格不在此象限
board[tr + s][tc + s - 1] = t; // t号骨牌覆盖象限最右上角
chessBoard(tr + s, tc, tr + s, tc + s - 1, s); // 将右上角视为特殊方格继续处理该象限
}
// 考虑右下角象限
if (dr >= tr + s && dc >= tc + s) {
// 特殊方格在此象限处理此象限
chessBoard(tr + s, tc + s, dr, dc, s);
} else {
// 特殊方格不在此象限
board[tr + s][tc + s] = t; // t号骨牌覆盖象限最左上角
chessBoard(tr + s, tc + s, tr + s, tc + s, s); // 将左上角视为特殊方格继续处理该象限
}
}
public static void main(String[] args) {
int k = 3;
int size = 1 << k;
Solution s = new Solution(size);
int tr = 1; // 特殊方格的行号
int tc = 2; // 特殊方格的列号
s.board[tr][tc] = 0; // 特殊方格用0表示
s.chessBoard(0, 0, tr, tc, size);
// 打印覆盖结果
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
System.out.print(s.board[i][j] + "\t");
}
System.out.println();
}
}
}
运行结果(0表示特殊方格的位置,3个相同数字代表一块骨牌)

时间复杂度分析
用 T ( k ) T(k) T(k)表示求解一个 2 k ∗ 2 k 2^k*2^k 2k∗2k棋盘的时间
- k = 1 k=1 k=1, T ( k ) = O ( 1 ) T(k)=Ο(1) T(k)=O(1)
- k > 1 k>1 k>1, T ( k ) = 4 T ( k − 1 ) T(k)=4T(k-1) T(k)=4T(k−1)
∴ T ( k ) = O ( 4 k ) \therefore T(k)=Ο(4^k) ∴T(k)=O(4k)
版权声明
本文为[atwdy]所创,转载请带上原文链接,感谢
https://blog.csdn.net/atwdy/article/details/119235066
边栏推荐
猜你喜欢
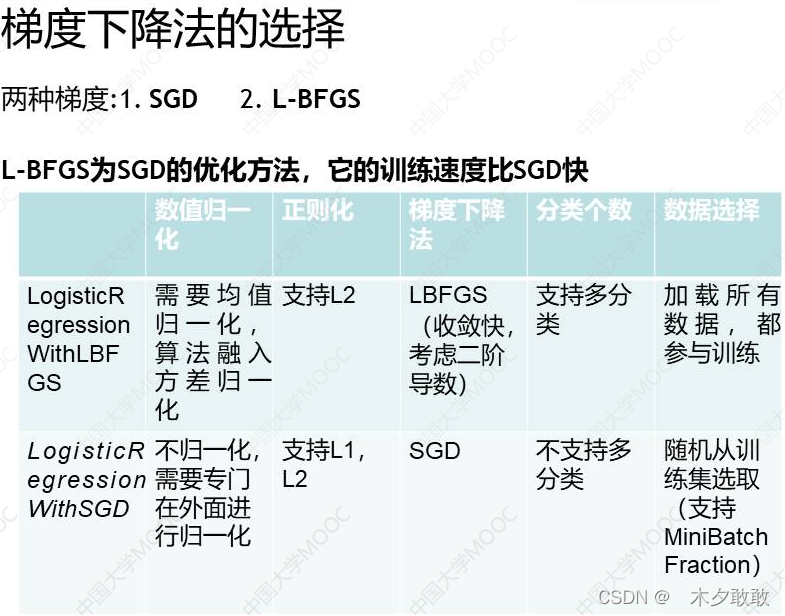
数据挖掘——逻辑回归

The breakpoint will not currently be hit No symbols have been loaded for this document.

LeetCode 467. 环绕字符串中唯一的子字符串 -- 动态规划

Exploration des données - regroupement
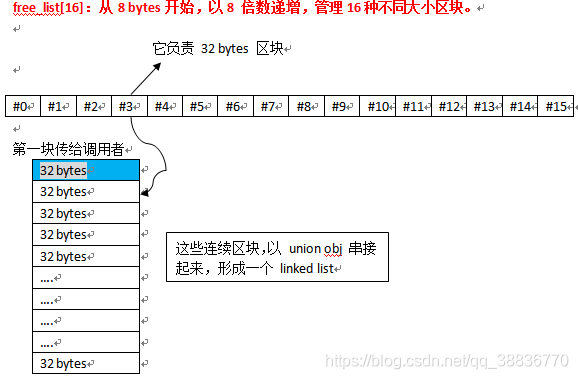
stl alloc 空间分配器 代码解析

01 knapsack problem (template)

Data mining -- data preprocessing
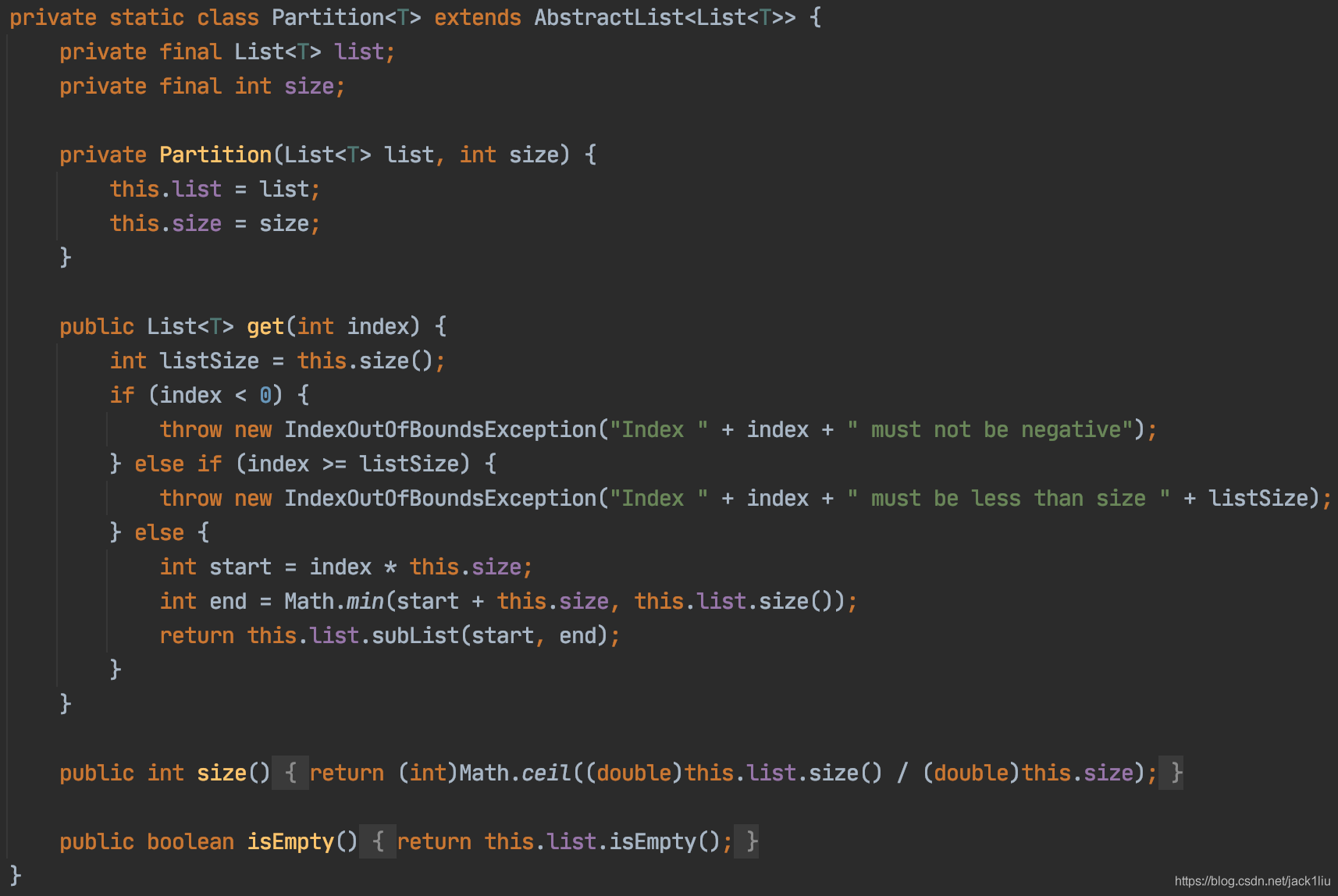
List分割最佳实践

MySQL basic commands and exercises (I)

数据挖掘——决策树分类
随机推荐
Error Putty X11 proxy: Authorisation not recognised
TCGA数据库ensembl id 转为 gene Symbol,提取出需要的RNA种类表达谱列表信息
集合和Map线程安全问题解决
线程池的几个常识
【机器学习】Scikit-learn介绍
mysql建表最佳实践
伪代码块编写(论文编写用)
数据已删除,又重新出现的问题排查
Force buckle 237 Delete specified node list
Force buckle 19 Delete the penultimate node of the linked list
RPC必知必会
JVM exploration
AcWing 836. 合并集合(并查集)
通过设置关联菜单建立excel记账本
raspberry keras-ocr can‘t allocate memory in static TLS block
Data mining -- decision tree classification
机器学习——用鸢尾花数据集画P-R曲线和ROC曲线
Data mining -- association rule mining
数据挖掘——逻辑回归
Circular linked list 2