当前位置:网站首页>SVM Support Vector Machine - Application of MATLAB in Mathematical Modeling
SVM Support Vector Machine - Application of MATLAB in Mathematical Modeling
2022-08-09 17:24:00 【YuNlear】
数据建模及MATLAB实现(三)
随着信息技术的发展和成熟,各行业积累的数据越来越多,因此需要通过数据建模的方法,从看似杂乱的海量数据中找到有用的信息.
支持向量机(SVM)
支持向量机(Support Vector Machine,SVM)It is a new generation of learning system based on statistical theory.SVMin a supervised learning manner,Divide the training set into categories,或者是预测新的训练点所对应的类别.
SVM基本思想
SVMThe goal is to construct a hyperplane that separates the two classes,And let this hyperplane maximize the split between the two classes.Separating the two classes by a large margin minimizes the expected generalization error——That is, when a new sample appears, the probability of misclassification is as small as possible.
一般来说,The middlemost partition between the two classes has the smallest probability of misclassification,因此,在SVM中,We also use a hyperplane between the two classes ω T x i + b = 0 \omega^Tx_i+b=0 ωTxi+b=0as two types of separators,而 ω T x i + b = α \omega^Tx_i+b=\alpha ωTxi+b=α与 ω T x i + b = − α \omega^Tx_i+b=-\alpha ωTxi+b=−αare two parallel boundary planes, respectively.boundary plane,i.e. a hyperplane parallel to the classifier plane and passing through at least one point in the dataset.But there are many choices of boundary planes,To make the hyperplane segmentation accurate,The distance between the two boundary planes needs to be maximized,That is, the edge is maximized.“通过SVM学习”The meaning is to find the hyperplane that maximizes the edge.
SVM理论基础
首先,Suppose there is a capacity of n n n的训练集样本 { ( x i , y i ) , i = 1 , 2 , ⋯ , n } \{(x_i,y_i),i=1,2,\cdots,n\} {(xi,yi),i=1,2,⋯,n}Consists of two categories,若 x i x_i xi属于第一类,则记 y i = 1 y_i=1 yi=1;若 x i x_i xi属于第二类,则记 y i = − 1 y_i=-1 yi=−1.
If there is a classification hyperplane:
ω T x i + b = 0 \omega^Tx_i+b=0 ωTxi+b=0
Then the samples can be correctly divided into two categories,That is, samples of the same class all fall on the same side of the classification hyperplane.即满足
{ ω T x i + b ≥ α y i = 1 ω T x i + b ≤ − α y i = − 1 α > 0 \left\{ \begin{aligned} \omega^Tx_i+b&\ge\alpha \ \ \ y_i=1\\ \omega^Tx_i+b&\le-\alpha \ \ \ y_i=-1\\ \alpha&>0 \end{aligned} \right. ⎩⎨⎧ωTxi+bωTxi+bα≥α yi=1≤−α yi=−1>0
两边同除以 α \alpha α则可表示为
{ ω T x i + b ≥ 1 y i = 1 ω T x i + b ≤ − 1 y i = − 1 \left\{ \begin{aligned} \omega^Tx_i+b&\ge1 \ \ \ y_i=1\\ \omega^Tx_i+b&\le-1 \ \ \ y_i=-1 \end{aligned} \right. { ωTxi+bωTxi+b≥1 yi=1≤−1 yi=−1
can be comprehensively expressed as
y i ( ω T x i + b ) ≥ 1 y_i(\omega^Tx_i+b)\ge1 yi(ωTxi+b)≥1
And the distance between the hyperplanes,That is, the edge can be represented as
2 ∣ ∣ ω T ∣ ∣ \frac{2}{||\omega^T||} ∣∣ωT∣∣2
Then the planning problem can be expressed as
m a x : 2 ∣ ∣ ω ∣ ∣ max:\frac{2}{||\omega||} max:∣∣ω∣∣2
Take the countdown
m i n : ∣ ∣ ω ∣ ∣ 2 min:\frac{||\omega||}{2} min:2∣∣ω∣∣
Get the final goal planning problem:
m i n : ∣ ∣ ω ∣ ∣ 2 s . t . y i ( ω T x i + b ) ≥ 1 min:||\omega||^2\\ s.t.\ \ \ \ y_i(\omega^Tx_i+b)\ge1 min:∣∣ω∣∣2s.t. yi(ωTxi+b)≥1
Finally, the Lagrange duality theory is used,Transform the problem into a dual problem,Solve using quadratic programming method,求得最优的 ω ∗ \omega^* ω∗和 b ∗ b^* b∗,Construct the optimal classification function f ( x ) f(x) f(x).
在输入空间中,If the data is not linearly separable,Support vector machines go through nonlinear mapping ∅ : R n → F \varnothing:R^n\rightarrow F ∅:Rn→FMap the data to some dot product space F F F,The above linear algorithm is then executed in the dot product space.在文献中,This function is called “核函数”.
支持向量机MATLAB程序设计
支持向量机MATLAB程序设计——SVM.m如下:
function [x,W,R]=SVM(X0)
for i=1:3
X(:,i)=(X0(:,i)-mean(X0(:,i)))/std(X0(:,i));
end
[m,n]=size(X);
e=ones(m,1);
D=[X0(:,4)];
B=zeros(m,m);
C=zeros(m,m);
for i =1:m
B(i,i)=1;
C(i,i)=D(i,1);
end
A=[-X(:,1).*D,-X(:,2).*D,-X(:,3).*D,D,-B];
b=-e;
f=[0,0,0,0,ones(1,m)];
lb=[-inf,-inf,-inf,-inf,zeros(1,m)]';
x=linprog(f,A,b,[],[],lb);
W=[x(1,1),x(2,1),x(3,1)];
CC=x(4,1);
R1=X*W'-CC;
R2=sign(R1);
R=[R1,R2];
边栏推荐
猜你喜欢
随机推荐
时间序列分析
面试经历(华为,瑞晟,大华,海康,虹软,顺丰)
CTF在线加解密以及常用工具
深入浅出最优化(6) 最小二乘问题的特殊方法
堆(heap)系列_0x03:堆块 + malloc/new底层 + LFH(WinDbg分析)
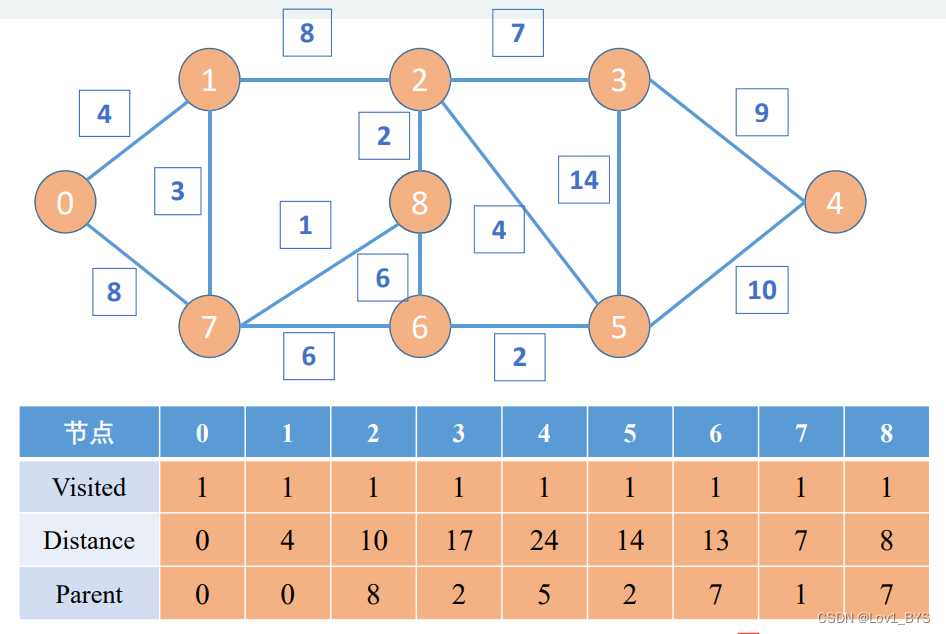
图论最短路径求解
Vim实用技巧_1.vim解决问题的方式
Vim practical skills_3. Visual mode and command mode
Vim practical skills_0.vim - introduction
【力扣】207. 课程表
Monte Carlo simulation
[Paper reading] LIME: Low-light Image Enhancement via Illumination Map Estimation (the most complete notes)
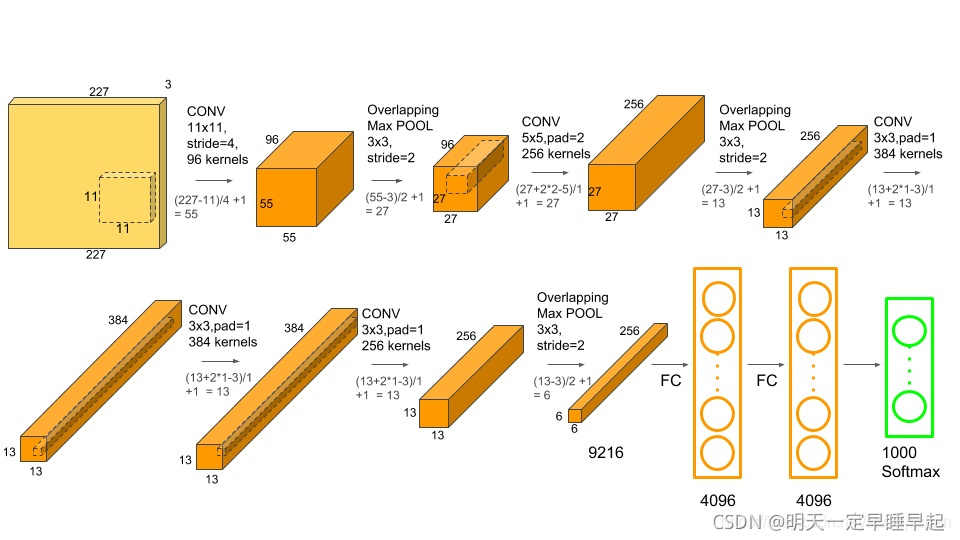
ResNet 残差网络 一些粗略的理解
LeNet5 pytorch实现
Basic Concepts of Software Security
【力扣】114. 二叉树展开为链表
godot正确设置2d像素游戏
Cloud Models and Logistic Regression - Applications of MATLAB in Mathematical Modeling (2nd Edition)
Virtualbox 设置共享文件夹
GO 使用 Protobuf实用指南