当前位置：网站首页>【八大排序④】归并排序、不基于比较的排序（计数排序、基数排序、桶排序）

【八大排序④】归并排序、不基于比较的排序（计数排序、基数排序、桶排序）

2022-08-09 09:34:00 【Living_Amethyst】

一、归并排序

二、计数排序

三、基数排序

四、桶排序

一、归并排序

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

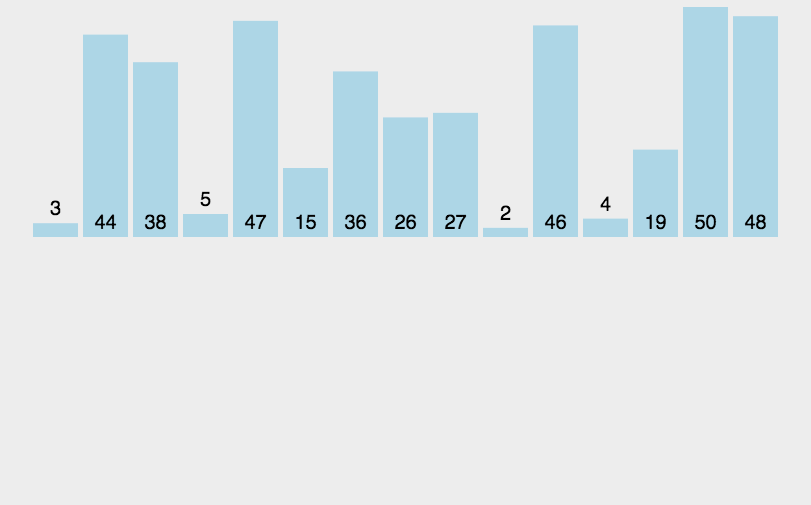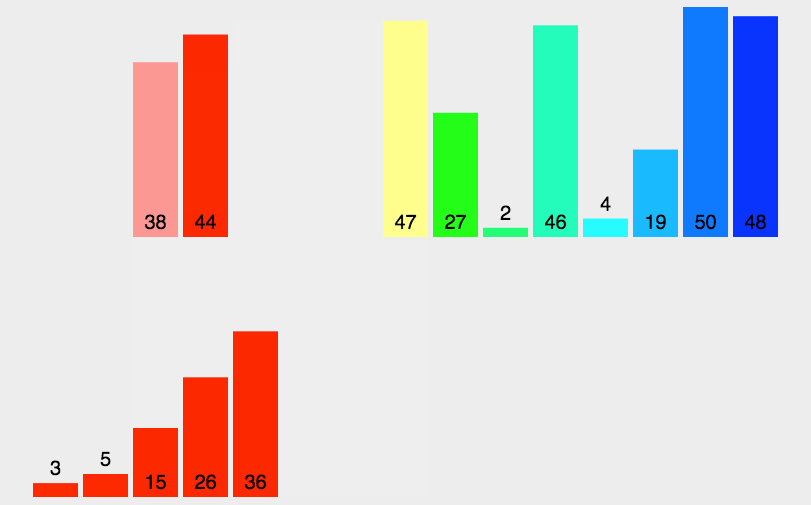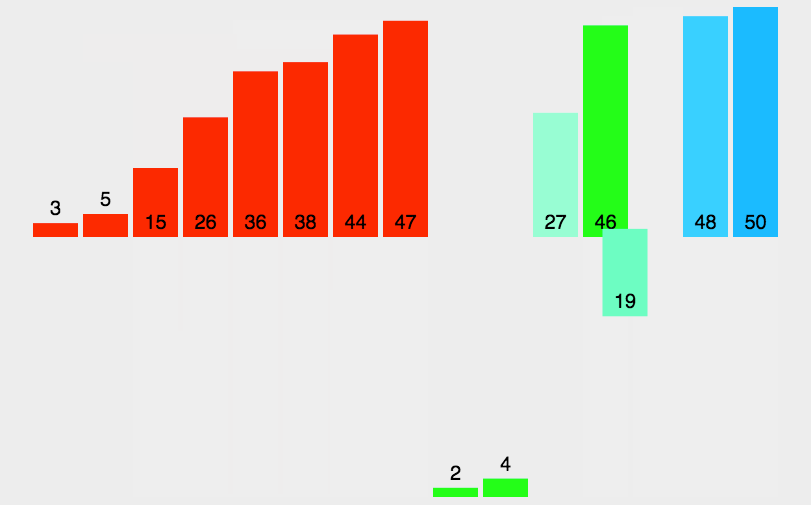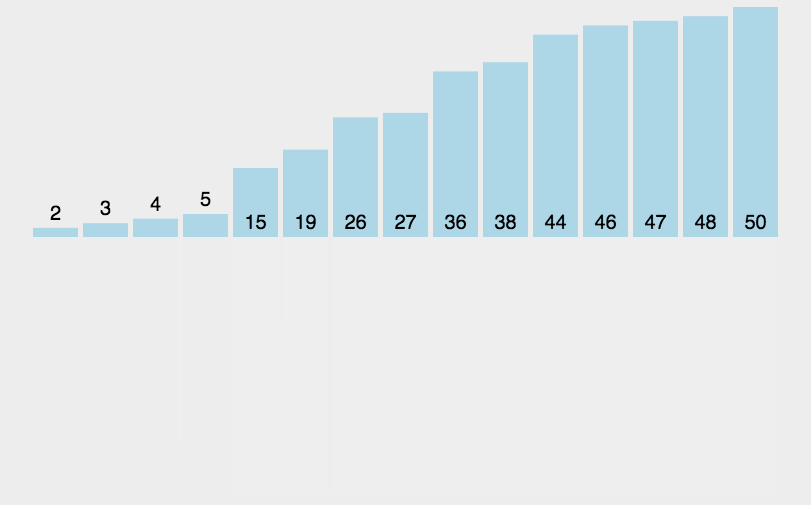
若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤：

分解
合并

代码（递归）

//归并排序
    public static void merge(int[] array,int low, int mid ,int high){
        int s1 = low;
        int e1 = mid;
        int s2 = mid+1;
        int e2 = high;
        int[] tmpArr = new int[high-low+1];
        int k = 0;
        //证明两个段都有数据
        while(s1 <= e1 && s2 <= e2){
            if(array[s1] < array[s2]){
                tmpArr[k++] = array[s1++];
            }else {
                tmpArr[k++] = array[s2++];
            }
        }
        while (s1 <= e1){
            tmpArr[k++] = array[s1++];
        }
        while (s2 <= e2){
            tmpArr[k++] = array[s2++];
        }

        for(int i = 0; i < k; i++){
            array[i+low] = tmpArr[i];
        }

    }
    public static void  mergeSortInternal(int[] array,int low, int high){
        if(low >= high) return;  //递归结束条件
        int mid = low + ((high-low) >>> 1) ;

        mergeSortInternal(array,low,mid);
        mergeSortInternal(array,mid+1,high);

        merge(array,low,mid,high);
    }
    public static void mergeSort(int[] array){
        mergeSortInternal(array,0,array.length-1);
    }

代码（非递归）

 public static void merge(int[] array,int low, int mid ,int high){
        int s1 = low;
        int e1 = mid;
        int s2 = mid+1;
        int e2 = high;
        int[] tmpArr = new int[high-low+1];
        int k = 0;
        //证明两个段都有数据
        while(s1 <= e1 && s2 <= e2){
            if(array[s1] < array[s2]){
                tmpArr[k++] = array[s1++];
            }else {
                tmpArr[k++] = array[s2++];
            }
        }
        while (s1 <= e1){
            tmpArr[k++] = array[s1++];
        }
        while (s2 <= e2){
            tmpArr[k++] = array[s2++];
        }

        for(int i = 0; i < k; i++){
            array[i+low] = tmpArr[i];
        }

    }
//归并排序（非递归）
    public static void mergeSortNor(int[] array){
        int gap = 1;
        while(gap < array.length){
            for(int i = 0; i < array.length; i += 2*gap){
                int left = i;
                int mid = left+gap-1;
                //修正mid，防止越界
                if(mid >= array.length){
                    mid = array.length-1;
                }
                int right = mid+gap;
                //修正right
                if(right >= array.length){
                    right = array.length-1;
                }
                merge(array,left,mid,right);
            }
        }
    }

归并排序总结
归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
时间复杂度：O(N*logN)
空间复杂度：O(N)
稳定性：稳定

二、计数排序

思想：计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。操作步骤：
1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中

算法的步骤如下：

（1）找出待排序的数组中最大和最小的元素
（2）统计数组中每个值为i的元素出现的次数，存入数组C的第i项
（3）对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）
（4）反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

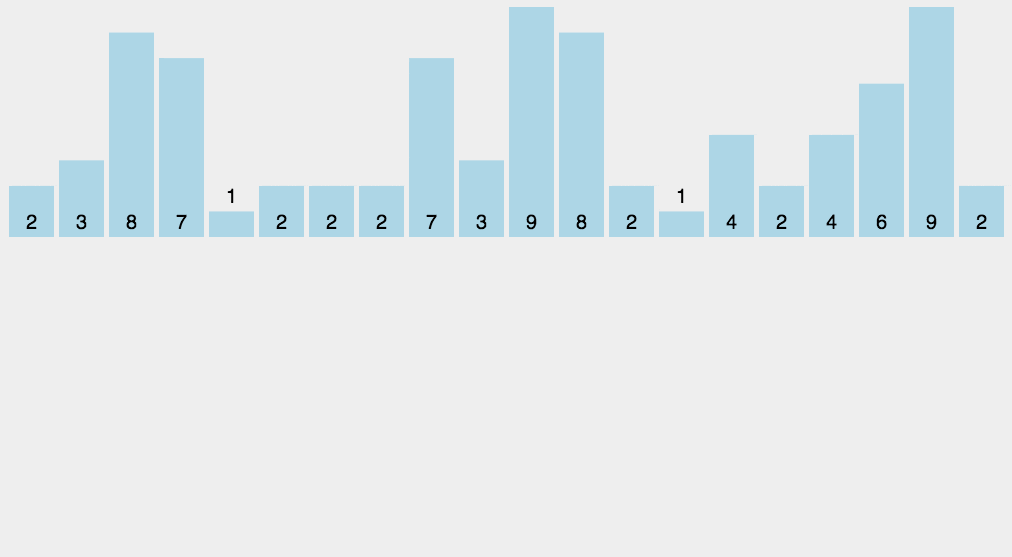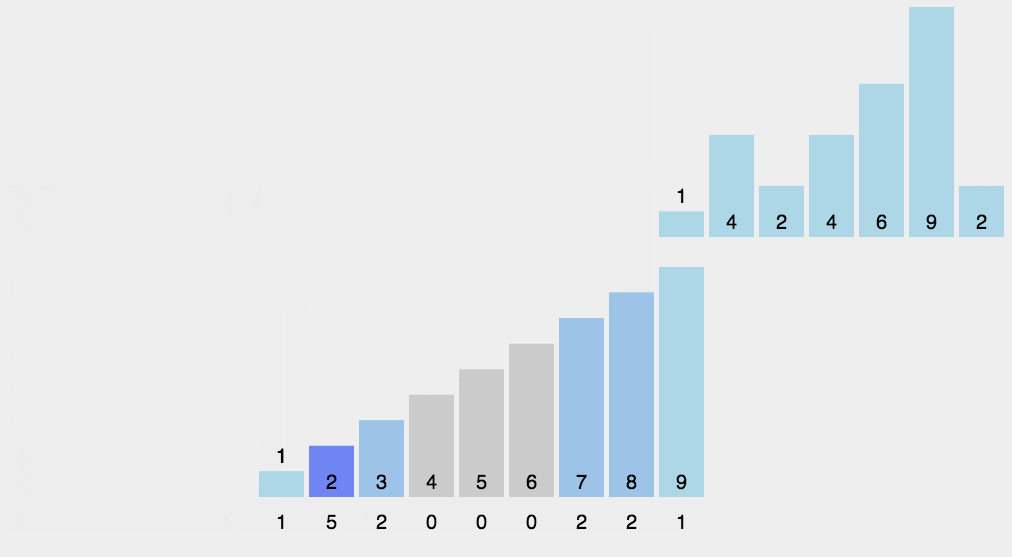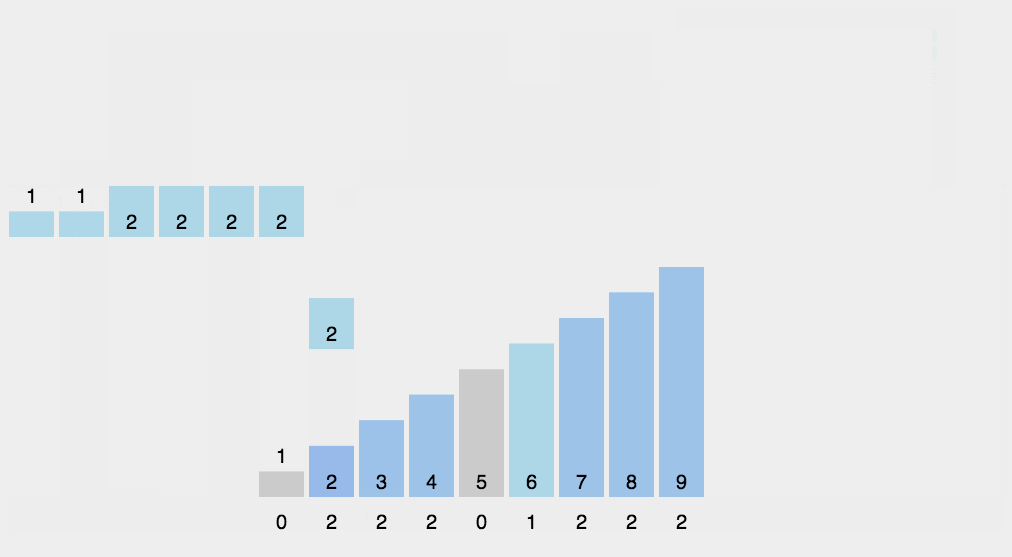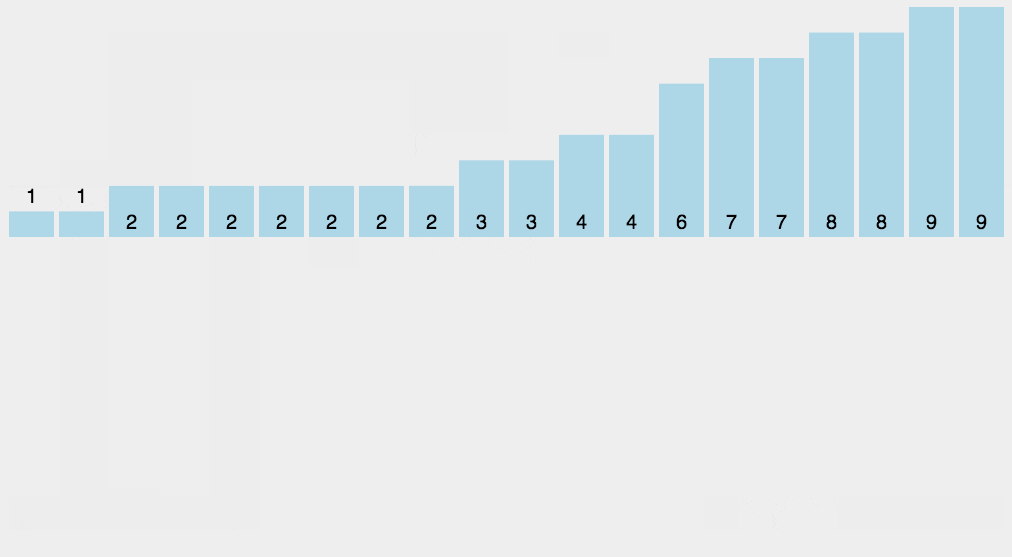
代码

   public static void countSort(int[] array){
        //1.获取最大值和最小值
        int maxVal = array[0];
        int minVal = array[0];
        for(int i = 1; i < array.length;i++){
            if(maxVal < array[i]){
                maxVal = array[i];
            }
            if(minVal > array[i]){
                minVal = array[i];
            }
        }
        //2.开始计数
        int range = maxVal-minVal+1;
        int[] count = new int[range];
        for (int i = 0; i < array.length; i++) {
            count[array[i] - minVal]++;
        }
        //3.遍历这个计数的数组，把数据放回array
        int index = 0;
        for (int i = 0; i < count.length; i++) {
            while(count[i]>0) {
                array[index++] = i + minVal;
                count[i]--;
            }
        }
    }

【计数排序的特性总结】
1. 计数排序在数据范围集中时，效率很高，但是适用范围及场景有限。
2. 时间复杂度：O(MAX(N,范围))
3. 空间复杂度：O(范围)
4. 稳定性：稳定