当前位置:网站首页>Educational Codeforces Round 81 (Rated for Div. 2)
Educational Codeforces Round 81 (Rated for Div. 2)
2022-04-23 09:41:00 【Zimba_】
A. Display The Number
The question :

Here you are. n ( 2 ⩽ n ⩽ 1 0 5 ) n(2\leqslant n\leqslant 10^{5}) n(2⩽n⩽105) A match , Ask the largest number you can spell .
Ideas :
Because matches with other numbers have to 4 4 4 More than , except 1 1 1 need 2 2 2 root , 7 7 7 need 3 3 3 root , So if you spell other numbers, you might as well spell two 1 1 1, and 3 3 3 When you put a match together 1 1 1 It's better to spell 7 7 7.
So when n n n For even when , Spell it all 1 1 1;
When n n n In an odd number of , Come out more 3 3 3 Root spell 7 7 7, All the others 1 1 1.
Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
int main()
{
ll T;
cin>>T;
while(T--)
{
ll n;
cin>>n;
if(n%2==0)
{
for(int i=1;i<=n/2;i++)putchar('1');
putchar('\n');
}
else
{
putchar('7');
for(int i=1;i<=n/2-1;i++)putchar('1');
putchar('\n');
}
}
return 0;
}
B. Infinite Prefixes
I was B The question card is out , A little speechless , Later, I thought about it .
The question :
Give you a length of n ( 1 ⩽ n ⩽ 1 0 5 ) n(1\leqslant n\leqslant 10^{5}) n(1⩽n⩽105) String of s s s, Define string t t t yes s s s Infinite cycle of .
Define the balance value of a prefix as 0 0 0 Number of minus 1 1 1 The number of , An empty string is a prefix .
Given a x ( − 1 0 9 ⩽ x ⩽ 1 0 9 ) x(-10^{9}\leqslant x \leqslant 10^{9}) x(−109⩽x⩽109).
Ask how many prefixes have a balanced value equal to x x x.
Ideas :
Let's deal with the whole string first s s s The equilibrium value of p p p.
Definition s s s The length in the string is i i i The balance value of the prefix of is w i w_{i} wi.
So what we need is the equation k p + w i = x kp+w_{i}=x kp+wi=x in , k k k How many natural number solutions are there .
The first p = 0 p=0 p=0 In the case of , Go through it. If it exists w i = x w_{i}=x wi=x There are infinite , Otherwise, 0 0 0 individual .
When p ≠ 0 p\neq 0 p=0 when , Got it. k = x − w i p k=\frac{x-w_{i}}{p} k=px−wi.
Then traverse i i i, For each of these w i w_{i} wi, if x − w i x-w_{i} x−wi Can be p p p to be divisible by , And calculated k k k For natural Numbers , Add... To the answer 1 1 1.
Last x = 0 x=0 x=0 when , Because empty strings need to be considered , So add 1 1 1.
Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
string s;
int main()
{
int T;
cin>>T;
while(T--)
{
ll n,x;
cin>>n>>x>>s;
ll p=0;
for(ll i=0;i<s.size();i++)
{
if(s[i]=='0')p++;
else p--;
}
if(p==0)
{
ll ans=0,w=0;
for(ll i=0;i<s.size();i++)
{
if(s[i]=='0')w++;
else w--;
if(w==x)ans++;
}
if(ans)cout<<-1<<endl;
else cout<<0<<endl;
continue;
}
ll ans=0,w=0;
for(ll i=0;i<s.size();i++)
{
if(s[i]=='0')w++;
else w--;
if((x-w)%p==0&&(x-w)/p>=0)ans++;
}
if(x==0)ans++;
cout<<ans<<endl;
}
return 0;
}
C. Obtain The String
The question :
Given a string s s s and t t t, The length range is 1 e 5 1e5 1e5.
You have an empty string , You want to construct a string t t t.
Every time you operate , You can start your s s s Select a subsequence , Add to your string .
Ask how many operations you need , You can construct a string t t t.
If it cannot be constructed, output − 1 -1 −1.
Ideas :
First , The situation that cannot be constructed can be judged directly , namely s s s Does not exist in the t t t A letter in .
Let's set a subscript to indicate s s s Location currently found in .
Then go through t t t Every single letter of , To be in s s s Quickly find the letter after the current position .
Then just preprocess out s s s At every position in the , The next position of each letter , You can find that letter quickly , Overall complexity o ( 26 × n ) o(26×n) o(26×n).
It's not easy to make it clear , See the code .
Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
string s,t;
int dp[100005][26];
int has[26];
int main()
{
int T;
cin>>T;
while(T--)
{
cin>>s>>t;
for(int i=0;i<26;i++)
{
has[i]=0;
dp[s.size()][i]=-1;
for(int j=s.size()-1;j>=0;j--)
{
has[s[j]-'a']=1;
if(s[j]=='a'+i)
{
dp[j][i]=j;
}
else dp[j][i]=dp[j+1][i];
}
}
int times=1,cur=0,ok=1;
for(int i=0;i<t.size();i++)
{
if(has[t[i]-'a']==0)
{
ok=0;break;
}
cur=dp[cur][t[i]-'a'];
if(cur==-1)
{
times++;
cur=dp[0][t[i]-'a']+1;
}
else
{
cur=dp[cur][t[i]-'a']+1;
}
}
if(ok==0)cout<<-1<<endl;
else cout<<times<<endl;
}
return 0;
}
D. Same GCDs
The question :
Given two numbers a a a and m m m. ( 1 ⩽ a < m ⩽ 1 0 10 ) (1\leqslant a<m\leqslant10^{10}) (1⩽a<m⩽1010)
How many x x x Satisfy 0 ⩽ x < m 0\leqslant x<m 0⩽x<m, And g c d ( a , m ) = g c d ( a + x , m ) gcd(a,m)=gcd(a+x,m) gcd(a,m)=gcd(a+x,m).
Ideas :
There was a loophole in the previous solution , So a new one .

So the final answer is m g c d ( a , m ) \frac{m}{gcd(a,m)} gcd(a,m)m The value of Euler's function , φ ( m g c d ( a , m ) ) \varphi(\frac{m}{gcd(a,m)}) φ(gcd(a,m)m).
Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
ll getPhi(ll n)
{
ll ans=n;
for(ll i=2;i*i<=n;i++)
{
if(n%i==0)
{
ans=ans/i*(i-1);
while(n%i==0)n/=i;
}
}
if(n>1)ans=ans/n*(n-1);
return ans;
}
ll gcd(ll a,ll b)
{
return b?gcd(b,a%b):a;
}
int main()
{
ll T;
scanf("%lld",&T);
while(T--)
{
ll a,m;
scanf("%lld%lld",&a,&m);
ll w=gcd(a,m);
ll ans=getPhi(m/w);
printf("%lld\n",ans);
}
return 0;
}
E. Permutation Separation
It's a little late to think of it , Just give me a little more time .
The question :
Given a 1 1 1 To n n n Permutation p 1 , p 2 … p n p_{1},p_{2}…p_{n} p1,p2…pn, And the cost of moving each location a i a_{i} ai.
( 2 ⩽ n ⩽ 2 × 1 0 5 , 1 ⩽ a i ⩽ 2 × 1 0 9 ) (2\leqslant n\leqslant2\times 10^{5},1\leqslant a_{i}\leqslant2\times 10^{9}) (2⩽n⩽2×105,1⩽ai⩽2×109)
Now you are required to divide it into two non empty sets , namely p 1 p 2 … p k p_{1}p_{2}…p_{k} p1p2…pk and p k + 1 p k + 2 … p n p_{k+1}p_{k+2}…p_{n} pk+1pk+2…pn.
Then select some elements on the left and move them to the right , Then select some elements on the right and move to the left , Finally, make any element on the right larger than any element on the left , If one side is empty, you can also .
Moving elements costs , Namely a i a_{i} ai.
Now ask how much you need at least , To meet the conditions .
Ideas :
I thought about it for a long time .
First first , Our answer takes a minimum value on the far left and right .
First , Now that you spend money to move , Then it doesn't matter , So instead, delete , The effect is the same .
Then we have to decide on a plan , There are two things to enumerate .
One is the boundary of segmentation , That is, the set boundary of the partition .
One is the divided number , That is, the maximum number on the left and the minimum number on the right have a boundary . let me put it another way , Anything larger than this on the left should be deleted , Anything smaller than this on the right should be deleted .
Obviously, the complexity of violent enumeration of these two is not enough , So let's consider enumerating one of them , Then quickly solve another .
Then you will find that the other one does not satisfy the dichotomy property .
Until I drew this picture on the draft book .
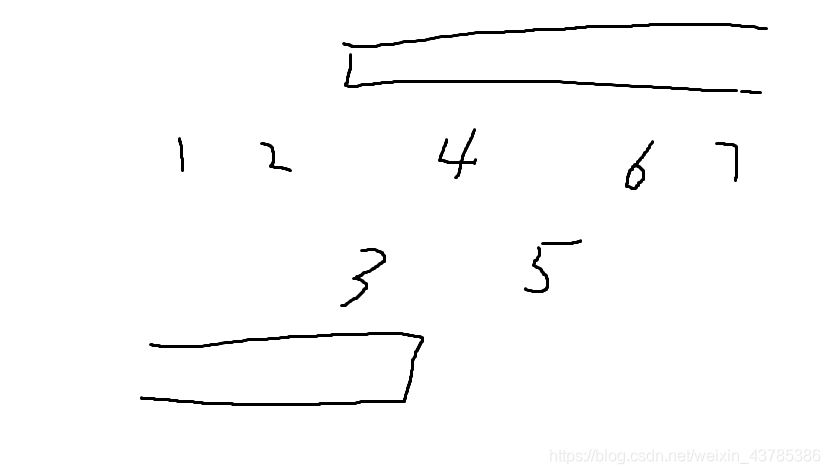
This picture actually gives a good solution to calculate the answer .
The numbers in the upper row represent the numbers divided into the set on the left .
A row of numbers divided on the right represents the set below .
Then we're going to enumerate 1 1 1 To 2 2 2 The gap between , 3 3 3 To 4 4 4 The gap between …… Calculate the smallest answer . And the calculation for each void is , The sum of the number in the upper row on the right of the gap plus the sum of the number in the lower row on the left of the gap .
Then for all the voids , We require a minimum .
So we need to use segment tree to maintain these gaps , And the update is also carried out in the interval .
Let's see how to update .
At first, the left set was only 1 1 1 Elements , On the right is n − 1 n-1 n−1 Elements .
Then we consider moving an element from the right to the left .
such as 3 3 3 Moved from the right set to the left set . We found that 3 3 3 When gathering on the right , The gap on the left will be added a 3 a_{3} a3, Now I've taken it from the right collection , So let him lose . And after moving to the left , Just give it to 3 3 3 Add... To the gap on the right a 3 a_{3} a3.
thus , Is a segment tree interval update , The template question of the most valuable query .
Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
ll tree[800005],laz[800005];
void push_down(ll k,ll l,ll r)
{
if(l==r)
{
tree[k]=tree[k]+laz[k];
laz[k]=0;
return ;
}
laz[2*k+1]=laz[2*k+1]+laz[k];
laz[2*k+2]=laz[2*k+2]+laz[k];
tree[k]=tree[k]+laz[k];
laz[k]=0;
}
void update(ll k,ll l,ll r,ll x,ll y,ll a)
{
push_down(k,l,r);
if(x<=l&&r<=y)
{
laz[k]=laz[k]+a;
return ;
}
ll mid=(l+r)/2;
if(x<=mid)update(2*k+1,l,mid,x,y,a);
if(y>=mid+1)update(2*k+2,mid+1,r,x,y,a);
push_down(2*k+1,l,mid);
push_down(2*k+2,mid+1,r);
tree[k]=min(tree[2*k+1],tree[2*k+2]);
}
ll query(ll k,ll l,ll r,ll x,ll y)
{
push_down(k,l,r);
if(x<=l&&r<=y)
{
return tree[k];
}
ll ans=1e18,mid=(l+r)/2;
if(x<=mid)ans=min(ans,query(2*k+1,l,mid,x,y));
if(y>=mid+1)ans=min(ans,query(2*k+2,mid+1,r,x,y));
return ans;
}
ll p[200005];
ll a[200005];
int main()
{
ll n;
scanf("%lld",&n);
for(ll i=1;i<=n;i++)scanf("%lld",&p[i]);
for(ll i=1;i<=n;i++)scanf("%lld",&a[i]);
ll ans=min(a[1],a[n]);
if(p[1]!=1)update(0,1,n-1,1,p[1]-1,a[1]);
for(ll i=2;i<=n;i++)if(p[i]!=n)update(0,1,n-1,p[i],n-1,a[i]);
ans=min(ans,query(0,1,n-1,1,n-1));
for(ll i=2;i<=n-1;i++)
{
if(p[i]!=n)update(0,1,n-1,p[i],n-1,-a[i]);
if(p[i]!=1)update(0,1,n-1,1,p[i]-1,a[i]);
ans=min(ans,query(0,1,n-1,1,n-1));
}
printf("%lld\n",ans);
return 0;
}
F. Good Contest
I didn't even look .
版权声明
本文为[Zimba_]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204230621425619.html
边栏推荐
- DVWA range practice
- Kettle experiment
- Cloud computing competition -- basic part of 2020 competition [task 3]
- Applet error: cannot read property'currenttarget'of undefined
- Golang force buckle leetcode 396 Rotation function
- Solving Lucas number and combination theorem
- kettle实验
- Kernel PWN learning (3) -- ret2user & kernel ROP & qwb2018 core
- Image processing in opencv -- Introduction to contour + contour features
- JS scope, scope chain, global variables and local variables
猜你喜欢

Redis exception read error on connection solution

SAP pi / PO function operation status monitoring and inspection
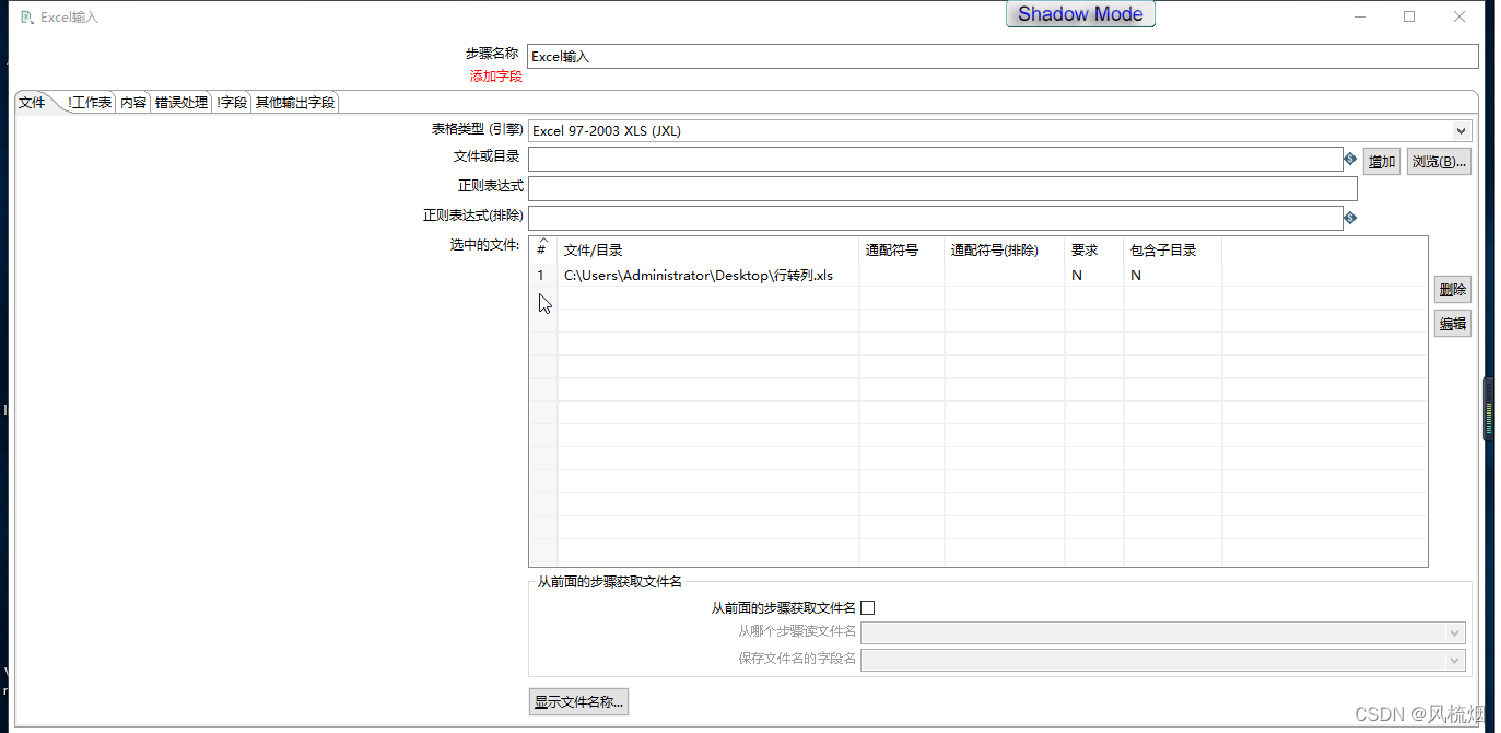
Kettle experiment (III)

#yyds干货盘点#ubuntu18.0.4安装mysql并解决ERROR 1698: Access denied for user ''root''@''localhost''

Personal homepage software fenrus

STM32 and FreeRTOS stack parsing

论文阅读《Integrity Monitoring Techniques for Vision Navigation Systems》——5结果

如何实现根据照片获取地理位置及如何防御照片泄漏地理位置
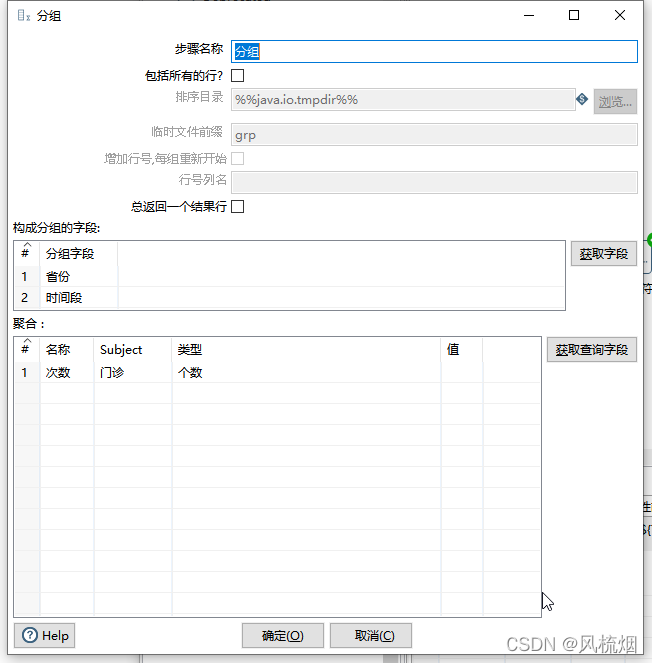
Kettle实验
![Sql1 [geek challenge 2019]](/img/ad/afca09bc1da003393319af700e90e3.png)
Sql1 [geek challenge 2019]
随机推荐
Installation of data cleaning ETL tool kettle
Summary of common concepts and problems of linear algebra in postgraduate entrance examination
Cloud computing competition -- basic part of 2020 competition [task 3]
JS and how to judge custom attributes in H5
Redis 异常 read error on connection 解决方案
Explanation of order and primitive root of number theory
三、6【Verilog HDL】基础知识之门级建模
Buuctf [actf2020 freshman competition] include1
数据清洗 ETL 工具Kettle的安装
Summary of wrong questions 1
Node installation
Yyds dry goods inventory ubuntu18 0.4 install MySQL and solve error 1698: access denied for user ''root' '@' 'localhost' '
501. 二叉搜索树中的众数
ASUS laptop can't read USB and surf the Internet after reinstalling the system
LeetCode 1611. The minimum number of operations to make an integer 0
Pre parsing of JS
Personal homepage software fenrus
ES-aggregation聚合分析
Set the maximum width of the body, but why does the background color of the body cover the whole page?
Random neurons and random depth of dropout Technology