当前位置:网站首页>Explanation of order and primitive root of number theory
Explanation of order and primitive root of number theory
2022-04-23 09:35:00 【Zimba_】
Preface :
I wanted to write BSGS Algorithm , however I want to play a game today I think it would be better to write the original root first , So let's focus on what is primordial root today 、 Which integers have original roots 、 Properties and solutions of primitive roots .
summary :
In order to reduce the hindsight , Just a quick introduction Euler function φ ( x ) \varphi(x) φ(x), The main part is followed by the introduction of the integral function .(ps: The symbol in the book says ϕ ( x ) \phi(x) ϕ(x), Yes, but online φ ( x ) \varphi(x) φ(x), But it doesn't matter )
Euler function φ ( x ) \varphi(x) φ(x) The function value of is , Less than x x x And with the x x x The number of Coprime positive integers .
such as φ ( 6 ) = 2 \varphi(6)=2 φ(6)=2, Because of less than 6 6 6 In the positive integer of , have only 1 1 1 And 5 5 5 With its mutual quality .
Easy to find , When p p p When it's a prime number , Yes φ ( x ) = p − 1 \varphi(x)=p-1 φ(x)=p−1.
And Euler's Theorem : if g c d ( a , n ) = 1 gcd(a,n)=1 gcd(a,n)=1, be a φ ( n ) ≡ 1 ( m o d p ) a^{\varphi(n)}\equiv1(mod\;p) aφ(n)≡1(modp).
About these first , To the body .
Order of integer :
What is step ?
set up a a a and n n n Is a coprime integer , a ≠ 0 , n > 0 a\neq 0,n>0 a=0,n>0, bring a x ≡ 1 ( m o d n ) a^{x}\equiv1(mod\;n) ax≡1(modn) The smallest positive integer established x x x, be called a a a model n n n The order of , The symbol is o r d n a ord_{n}a ordna.
For example, requirements 2 2 2 model 7 7 7 The order of , Let's list them one by one ,
2 1 ≡ 2 ( m o d 7 ) , 2 2 ≡ 4 ( m o d 7 ) , 2 3 ≡ 1 ( m o d 7 ) 2^{1}\equiv2(mod\;7),2^{2}\equiv4(mod\;7),2^{3}\equiv1(mod\;7) 21≡2(mod7),22≡4(mod7),23≡1(mod7).
Then we call 2 2 2 model 7 7 7 The order is 3 3 3, Write it down as o r d 7 2 = 3 ord_{7}2=3 ord72=3.
Now let's look at the equation a x ≡ 1 ( m o d n ) a^{x}\equiv1(mod\;n) ax≡1(modn).
So obviously according to Euler's Theorem , We can know φ ( n ) \varphi(n) φ(n) It's a solution to the equation , But it is not necessarily the smallest , So it's not necessarily order , And when φ ( n ) \varphi(n) φ(n) yes a a a model n n n Order time of , We call a a a by n n n One of the original roots , This will be introduced later .
Now let's go on .
A theorem : if g c d ( a , n ) = 1 gcd(a,n)=1 gcd(a,n)=1, be x 0 x_{0} x0 It's the equation a x ≡ 1 ( m o d n ) a^{x}\equiv1(mod\;n) ax≡1(modn) The necessary and sufficient condition for a solution of is o r d n a ∣ x ord_{n}a|x ordna∣x.( among ∣ | ∣ It's an integer division sign , Express o r d n a ord_{n}a ordna to be divisible by x x x)
This necessity is well proved , since a o r d n a ≡ 1 ( m o d n ) a^{ord_{n}a}\equiv1(mod\;n) aordna≡1(modn), that a k × o r d n a ≡ 1 ( m o d n ) a^{k\times ord_{n}a}\equiv1(mod\;n) ak×ordna≡1(modn) Of course, it also holds true .
Then sufficiency , Suppose there is x 1 x1 x1 Not divisible x 0 x_{0} x0 And satisfy the equation , Make x 1 = k × o r d n a + d x_{1}=k\times ord_{n}a+d x1=k×ordna+d( among d d d Not divisible o r d n a ord_{n}a ordna) Satisfy the equation , that d d d Certain ratio o r d n a ord_{n}a ordna Small , And meet a d ≡ 1 ( m o d n ) a^{d}\equiv1(mod\;n) ad≡1(modn), Then it's the original root .
This proves that .
Theorem 2 : if g c d ( a , n ) = 1 gcd(a,n)=1 gcd(a,n)=1, be o r d n a ord_{n}a ordna aliquot φ ( n ) \varphi(n) φ(n).
From the front, you can also think of , And it is obvious from theorem 1 .
At this time, it is easy to think of one o ( n l o g ) o(\sqrt{n} log) o(nlog) The way to find the order , because n n n The order of must be φ ( n ) \varphi(n) φ(n) Factor of , So we can enumerate its factors , Let's see if the conditions are met .
Theorem 3 : if g c d ( a , n ) = 1 gcd(a,n)=1 gcd(a,n)=1, be a i ≡ a j ( m o d n ) a^i\equiv a^j(mod\;n) ai≡aj(modn) If and only if i ≡ j ( m o d o r d n a ) i\equiv j(mod\;ord_{n}a) i≡j(modordna).
Theorem is more important , Think about it yourself .
Theorem 4 : if o r d n a = t ord_{n}a=t ordna=t, And u u u As a positive integer , Then there are o r d n ( a u ) = t g c d ( t , u ) ord_{n}(a^{u})=\frac{t}{gcd(t,u)} ordn(au)=gcd(t,u)t .
For example, experience , 2 3 ≡ 1 ( m o d 7 ) 2^3\equiv1(mod\;7) 23≡1(mod7), Then there is 8 1 ≡ 1 ( m o d 7 ) 8^1\equiv1(mod\;7) 81≡1(mod7). That's what it is 3 3 3 Factor of , It's much easier to understand in this way .
Primordial root :
When a a a model n n n The order is φ ( n ) \varphi(n) φ(n), That is to say, if and only if x x x yes φ ( n ) \varphi(n) φ(n) Multiple , bring a x ≡ 1 ( m o d n ) a^{x}\equiv1(mod\;n) ax≡1(modn) establish , At this time said a a a by n n n The original root .
So I know n n n The original root a a a after , What are the benefits , Let me give you an example .
Let's take 998244353 The original root 3, Let's take a prime number 7 7 7 One of the original roots 3 3 3, Then list 3 3 3 Power module of 7 7 7.
3 1 ≡ 3 ( m o d 7 ) , 3 2 ≡ 2 ( m o d 7 ) , 3 3 ≡ 6 ( m o d 7 ) , 3 4 ≡ 4 ( m o d 7 ) , 3 5 ≡ 5 ( m o d 7 ) , 3 6 ≡ 1 ( m o d 7 ) 3^{1}\equiv3(mod\;7),3^{2}\equiv2(mod\;7),3^{3}\equiv6(mod\;7),3^{4}\equiv4(mod\;7),3^{5}\equiv5(mod\;7),3^{6}\equiv1(mod\;7) 31≡3(mod7),32≡2(mod7),33≡6(mod7),34≡4(mod7),35≡5(mod7),36≡1(mod7).
Then it is found that these residuals form a module 7 7 7 The complete residue system of 1 , 2 , 3 , 4 , 5 , 6 1,2,3,4,5,6 1,2,3,4,5,6, That is, for any a a a, Can be found x 0 x_{0} x0 bring 3 x 0 ≡ a ( m o d 7 ) 3^{x_{0}}\equiv a(mod\;7) 3x0≡a(mod7).
This is the case of prime numbers , Now let's look at the case of Kangkang non prime numbers , for 18 18 18 One of the original roots 5 5 5. Then list 5 5 5 Power module of 18 18 18.
5 1 ≡ 5 ( m o d 18 ) , 5^{1}\equiv5(mod\;18), 51≡5(mod18),
5 2 ≡ 7 ( m o d 18 ) , 5^{2}\equiv7(mod\;18), 52≡7(mod18),
5 3 ≡ 17 ( m o d 18 ) , 5^{3}\equiv17(mod\;18), 53≡17(mod18),
5 4 ≡ 13 ( m o d 18 ) , 5^{4}\equiv13(mod\;18), 54≡13(mod18),
5 5 ≡ 11 ( m o d 18 ) , 5^{5}\equiv11(mod\;18), 55≡11(mod18),
5 6 ≡ 1 ( m o d 18 ) . 5^{6}\equiv1(mod\;18). 56≡1(mod18).
5 7 ≡ 5 ( m o d 18 ) , 5^{7}\equiv5(mod\;18), 57≡5(mod18),
5 8 ≡ 7 ( m o d 18 ) , 5^{8}\equiv7(mod\;18), 58≡7(mod18),
5 9 ≡ 17 ( m o d 18 ) , 5^{9}\equiv17(mod\;18), 59≡17(mod18),
5 10 ≡ 13 ( m o d 18 ) , 5^{10}\equiv13(mod\;18), 510≡13(mod18),
5 11 ≡ 11 ( m o d 18 ) , 5^{11}\equiv11(mod\;18), 511≡11(mod18),
5 12 ≡ 1 ( m o d 18 ) . 5^{12}\equiv1(mod\;18). 512≡1(mod18).
5 13 ≡ 5 ( m o d 18 ) , 5^{13}\equiv5(mod\;18), 513≡5(mod18),
5 14 ≡ 7 ( m o d 18 ) , 5^{14}\equiv7(mod\;18), 514≡7(mod18),
5 15 ≡ 17 ( m o d 18 ) , 5^{15}\equiv17(mod\;18), 515≡17(mod18),
5 16 ≡ 13 ( m o d 18 ) , 5^{16}\equiv13(mod\;18), 516≡13(mod18),
5 17 ≡ 11 ( m o d 18 ) , 5^{17}\equiv11(mod\;18), 517≡11(mod18),
5 18 ≡ 1 ( m o d 18 ) . 5^{18}\equiv1(mod\;18). 518≡1(mod18).
It is easy to find that 6 6 6 One for a group , So this one 6 6 6 What is it? ?
It's actually φ ( 18 ) = 6 \varphi(18)=6 φ(18)=6. Then the number appears 1 , 5 , 7 , 11 , 13 , 17 1,5,7,11,13,17 1,5,7,11,13,17, It is with 18 18 18 Coprime 6 6 6 How many .
Then the case of prime numbers above makes sense .
So we can get ,
A theorem : if g c d ( a , n ) = 1 gcd(a,n)=1 gcd(a,n)=1, be a 1 , a 2 , … … , a φ ( n ) a^{1},a^{2},……,a^{\varphi(n)} a1,a2,……,aφ(n) Form a mold n n n The irreducible residue system of .
If you understand it, you won't prove it .
And when p p p When it's a prime number , We can solve the equation x 5 ≡ a ( m o d p ) x^{5}\equiv a(mod\;p) x5≡a(modp) The problem is replaced by solving g 5 x ≡ a ( m o d p ) g^{5x}\equiv a(mod\;p) g5x≡a(modp), among g g g yes p p p The original root , because g g g The power of is a module n n n The complete residue system of , So it can be used g x g^{x} gx To replace x x x, In this way, we only ask for the of the new equation x 0 x_{0} x0, Then the solution of the original equation can be found .
next ,
Theorem 2 : If a number n n n It has roots , So how many different primitive roots does he have ,
The answer is φ ( φ ( n ) ) \varphi(\varphi(n)) φ(φ(n)) individual .
False proof : From the previous order, theorem 4 , We can know o r d n ( a u ) = t g c d ( t , u ) ord_{n}(a^{u})=\frac{t}{gcd(t,u)} ordn(au)=gcd(t,u)t, So when a a a by n n n The original root of , There is o r d n a = φ ( n ) ord_{n}a=\varphi(n) ordna=φ(n).
So we get , o r d n ( a u ) = φ ( n ) g c d ( φ ( n ) , u ) ord_{n}(a^{u})=\frac{\varphi(n)}{gcd(\varphi(n),u)} ordn(au)=gcd(φ(n),u)φ(n).
So we should make o r d n ( a u ) ord_{n}(a^{u}) ordn(au) be equal to φ ( n ) \varphi(n) φ(n), It's about meeting g c d ( φ ( n ) , u ) gcd(\varphi(n),u) gcd(φ(n),u), stay 1 1 1 To φ ( n ) − 1 \varphi(n)-1 φ(n)−1 Naturally, there are φ ( φ ( n ) ) \varphi(\varphi(n)) φ(φ(n)) One that meets the conditions .
Eating out , Come back and write .
Now study which numbers have primitive roots , That is to say The existence of primitive roots .
Because I just had dinner , I'm lazy .
First prove that prime numbers have primitive roots .
Then prove that the powers of odd prime numbers have primitive roots .
Then discuss about 2 2 2 The power of , Find out 2 2 2 and 4 4 4 It has primitive roots , other 2 2 2 There is no primitive root to the power of .
And then find out 2 2 2 The power of the odd prime number also has the original root .
Finally, prove that the rest have no original root .
therefore , Come to the conclusion :
Theorem 3 : 2 2 2 and 4 4 4, And the positive integer power of odd prime numbers p k p^{k} pk, as well as 2 2 2 Multiply by the positive integer power of odd prime number 2 p k 2p^{k} 2pk They all have primitive roots .
Last , Study how to find p p p The original root . Portal
First give a solution to violence .( There is no second )
First judge whether there is an original root .
2 2 2 The original root of is 1 1 1, 3 3 3 The original root of is 2, 4 4 4 The original root of is 3 3 3 Direct special judgment .
Then we enumerate violence [ 2 , p − 1 ] [2,p-1] [2,p−1], Then judge whether it is p p p The original root , When enumerating, of course, it is necessary to ensure mutual quality with modules .
As for judging i i i Is it right? p p p The original root , Just see if it exists x 0 x_{0} x0 Than φ ( p ) \varphi(p) φ(p) Small , And meet i x 0 ≡ 1 ( m o d p ) i^{x_{0}}\equiv 1(mod\;p) ix0≡1(modp).
But we're not going to enumerate one by one x 0 x_{0} x0, Because we know that its order satisfies the equation , And the multiple of order also satisfies the equation . So we just need to φ ( p ) \varphi(p) φ(p) The qualitative factor is decomposed into p 1 k 1 p 2 k 2 … p n k n p_{1}^{k_{1}}p_{2}^{k_{2}}…p_{n}^{k_{n}} p1k1p2k2…pnkn.
Then enumerate each prime factor , Judge whether it exists i φ ( p ) p j ≡ 1 ( m o d p ) i^{\frac{\varphi(p)}{p_{j}}}\equiv1(mod\;p) ipjφ(p)≡1(modp). If exist , Description order ratio φ ( p ) \varphi(p) φ(p) Small , Is not the original root ; conversely , Is the original root .
Do wonders vigorously , Worthy of great efforts .
Finally, post the code :
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
ll gcd(ll a,ll b)
{
return b?gcd(b,a%b):a;
}
ll fpow(ll a,ll n,ll p)
{
ll sum=1,base=a%p;
while(n!=0)
{
if(n%2)sum=sum*base%p;
base=base*base%p;
n/=2;
}
return sum;
}
vector<ll> getPrimFac(ll n)
{
vector<ll>fac;
fac.clear();
for(ll i=2;i*i<=n;i++)
{
if(n%i==0)
{
fac.push_back(i);
while(n%i==0)n/=i;
}
}
if(n>1)fac.push_back(n);
return fac;
}
bool hasRoot(ll n)
{
if(n==2||n==4)return true;
if(n<=1||n%4==0)return false;
ll num=0;
while(n%2==0)n/=2;
for(ll i=3;i*i<=n;i++)
{
if(n%i==0)
{
num++;
while(n%i==0)n/=i;
}
}
if(n>1)num++;
if(num==1)return true;
return false;
}
ll getPhi(ll n)
{
ll ans=n;
for(ll i=2;i*i<=n;i++)
{
if(n%i==0)
{
ans=ans/i*(i-1);
while(n%i==0)n/=i;
}
}
if(n>1)ans=ans/n*(n-1);
return ans;
}
ll getRoot(ll n)
{
if(!hasRoot(n))return -1;// There is no original root. Return -1
if(n==2)return 1;
if(n==3)return 2;
if(n==4)return 3;
ll w=getPhi(n);
vector<ll>fac=getPrimFac(w);
for(ll i=2;i<w;i++)
{
if(gcd(i,n)!=1)continue;
ll is=1;
for(ll j=0;j<fac.size();j++)
{
if(fpow(i,w/fac[j],n)==1)is=0;
}
if(is)return i;
}
return -1;
}
int main()
{
ll p;
scanf("%lld",&p);
printf("%lld\n",getRoot(p));
return 0;
}
版权声明
本文为[Zimba_]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204230621425681.html
边栏推荐
- JS prototype chain
- Acquisition of DOM learning elements JS
- Pre parsing of JS
- Kettle experiment (III)
- kettle庖丁解牛第14篇之JSON输入
- Emuelec compilation summary
- Colorui solves the problem of blocking content in bottom navigation
- Redis expired key cleaning and deletion policy summary
- Two methods of building Yum source warehouse locally
- Flink 流批一体在小米的实践
猜你喜欢
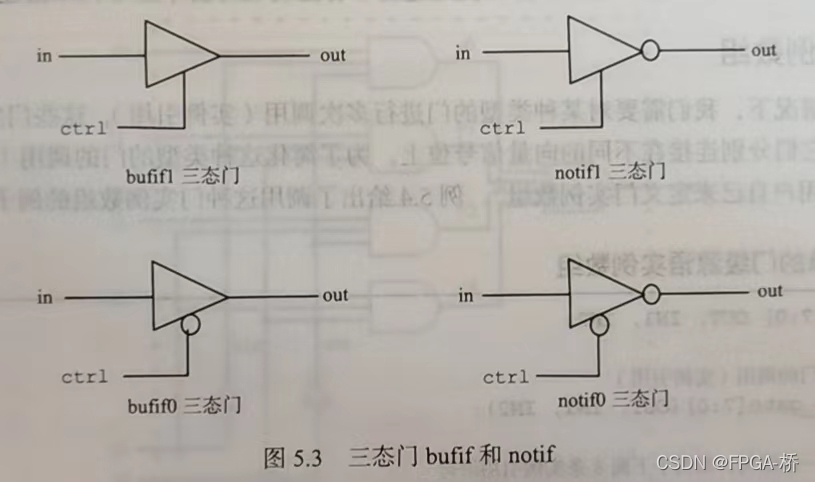
三、6【Verilog HDL】基础知识之门级建模

Summary of wrong questions 1
![[reading notes] Chapter 5 conditional statements, circular statements and block statements of Verilog digital system design tutorial (with answers to thinking questions)](/img/a2/b50fadad859a050eecfa15a436e126.png)
[reading notes] Chapter 5 conditional statements, circular statements and block statements of Verilog digital system design tutorial (with answers to thinking questions)

Practice of Flink streaming batch integration in Xiaomi

Simple understanding of arguments in JS
Canary publishing using ingress

112. 路径总和

kettle实验

Amazon cloud technology entry Resource Center, easy access to the cloud from 0 to 1
![[geek challenge 2019] havefun1](/img/8b/b15bf31771d54db25f24d630e64093.png)
[geek challenge 2019] havefun1
随机推荐
JS DOM learn three ways to create elements
3、 6 [Verilog HDL] gate level modeling of basic knowledge
员工试用期转正申请书(泸州老窖)
Kettle实验 (三)
Two ways for flutter providers to share data
Redis expired key cleaning and deletion policy summary
Cross domain configuration error: when allowcredentials is true, allowedorigins cannot contain the special value "*“
Kettle experiment (III)
Three ways to create objects in JS
501. 二叉搜索树中的众数
SAP 03-amdp CDs table function using 'with' clause
JS node operation, why learn node operation
112. 路径总和
Kettle experiment
653. 两数之和 IV - 输入 BST
RSA encryption and decryption signature verification
个人主页软件Fenrus
Wechat applet catchtap = "todetail" event problem
《数字电子技术基础》3.1 门电路概述、3.2 半导体二极管门电路
Pre parsing of JS