当前位置:网站首页>Hessian Matrix 海森矩阵
Hessian Matrix 海森矩阵
2022-08-09 19:55:00 【为为为什么】
海森矩阵是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。
简介
海森矩阵(Hessian Matrix),又译作黑塞矩阵、海瑟矩阵、海塞矩阵等,是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。海森矩阵最早于19世纪由德国数学家Ludwig Otto Hesse提出,并以其名字命名。海森矩阵常用于牛顿法解决优化问题。
定义
- 对于一个实值多元函数 f\left(x_ {1}, x_ {2}, \cdots, x_ {n}\right) , 如果函数 f 的二阶偏导数都存在, 则定义 f 的海森矩阵为
- 其中 D_ {i} 表示对第 i 个变量的微分算子, \vec {x}=\left(x_ {1}, x_ {2}, \cdots, x_ {n}\right) 。那么, f 的海森矩阵即
与泰勒展开项的关系
- 海森矩阵也可以理解为多元函数泰勒展开后的二阶导系数矩阵
二元函数
- 若一元函数 f(x) 在 x=x^ {(0)} 点的某个邻域内具有任意阶导数,则 f(x) 在 x^ {(0)} 点处的泰勒展开式 为:
- 其中 \Delta x=x-x^ {(0)} , \Delta x^ {2}=\left(x-x^ {(0)}\right)^ {2} 。 二元函数 f\left(x_ {1}, x_ {2}\right) 在 X^ {(0)}\left(x_ {1}^ {(0)}, x_ {2} ^ {(0)} \right) 点处的泰勒展开式为:
其中, \Delta x_ {1}=x_ {1}-x_ {1}^ {(0)}, \Delta x_ {2}==x_ {2}-x_ {2}^ {(0)} 。
将上述展开式写成矩阵形式,则有:
- G\left(X^ {(0)}\right) 是 f\left(x_ {1}, x_ {2}\right) 在 X^ {(0)} 点处的黑塞矩阵。它是由函数 f\left(x_ {1}, x_ {2}\right) 在 X^ {(0)} 点处的二阶偏导数所组成的方阵。
多元函数
- 将二元函数的泰勒展开式推广到多元函数
点处的泰勒展开式的矩阵形式为:
其中:
- \nabla f\left(X^ {(0)}\right)=\left.\left[\frac {\partial f} {\partial x_ {1}}, \frac {\partial f} {\partial x_ {2}}, \cdots, \frac {\partial f} {\partial x_ {n}}\right]\right|_ {X^ {(0)}} ^ {T} ,它是 f(X) 在 X^ {(0)} 点处的梯度。
- G\left(X^ {(0)}\right)=\left[\begin {array} {cccc}\frac {\partial^ {2} f} {\partial x_ {1}^ {2}} & \frac {\partial^ {2} f} {\partial x_ {1} \partial x_ {2}} & \cdots & \frac {\partial^ {2} f} {\partial x_ {1} \partial x_ {n}} \\ \frac {\partial^ {2} f} {\partial x_ {2} \partial x_ {1}} & \frac {\partial^ {2} f} {\partial x_ {2}^ {2}} & \cdots & \frac {\partial^ {2} f} {\partial x_ {2} \partial x_ {n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac {\partial^ {2} f} {\partial x_ {n} \partial x_ {1}} & \frac {\partial^ {2} f} {\partial x_ {n} \partial x_ {2}} & \cdots & \frac {\partial^ {2} f} {\partial x_ {n}^ {2}}\end {array}\right]_ {X^ {(0)}} f(X) 在 X^ {(0)} 点处的黑塞矩阵。
- 黑塞矩阵是由目标函数 f 在点X处的二阶偏导数组成的 n \times n 阶对称矩阵。
性质
对称性
- 如果函数 f 在 D 区域内二阶连续可导, 那么 f 海森矩阵 H(f) 在 D 内为对称矩阵。原因是: 如果函数 f 的二阶偏导数连 续, 则二阶偏导数的求导顺序汥有区别, 即
- 则对于矩阵 H(f) , 有 H_ {i, j}(f)=H_ {j, i}(f) , 所以 H(f) 为对称矩阵。
极值判定
- 如果实值多元函数 f\left(x_ {1}, x_ {2}, \cdots, x_ {n}\right) 二阶连续可导, 并且在临界点 M\left(x_ {i}\right) (其中 i=1,2, \cdots, n , 并且 x_ {i} 已知) 处梯度 (一阶导数) 等于 0 , 即 \nabla f(M)=0, M 为驻点。仅通过一阶导数无法判断在临界点, M 处是极大值还是极小值。
- 记 f 在 M 点处的海森矩阵为 H(M) 。由于 f 在 M 点处连续, 所以 H(M) 是一个 n \times n 的对称矩阵。对于 H(M) , 有 如下结论:
- 如果 H(M) 是正定矩阵, 则临界点 M 处是一个局部的极小值。
- 如果 H(M) 是负定矩阵, 则临界点M处是一个局部的极大值。
- 如果 H(M) 是不定矩阵, 则临界点 M 处不是极值。
- 当 H(M) 为半正定矩阵或半负定矩阵时, 临界点 M 是“可疑”极值点,尚需要利用其他方法来判定。
参考资料
边栏推荐
- 【NOI模拟赛】防AK题(生成函数,单位根,Pollard-Rho)
- [Essay] To the friends of the 19th issue
- 消防安全培训|“蓝朋友”,开课了!
- Application of Acrel5000web Energy Consumption System in a College-Susie Week
- 10个 Istio 流量管理 最常用的例子,你知道几个?
- Transformer如何用于3D视觉?阿联酋MBZUAI最新《3D视觉Transformers处理》综述,涵盖100+种方法
- 不经意传输协议OT
- 普源精电上半年扭亏为盈,高端产品持续发力!你看好仪器界“华为”吗?
- 钢材行业供应链协同管理系统提升企业上下游密切度,精细化企业内部管理
- 2.2 监督学习-1
猜你喜欢

Access control knowledge

力扣15-三数之和——HashSet&双指针法

buuctf(探险2)

DSPE-PEG-Azide,DSPE-PEG-N3,磷脂-聚乙二醇-叠氮可和DBCO直接反应

DSPE-PEG-PDP,DSPE-PEG-OPSS,磷脂-聚乙二醇-巯基吡啶可减少肽的免疫原性

访问控制知识

MySQL, which is asked on both sides of the byte, almost didn't answer well
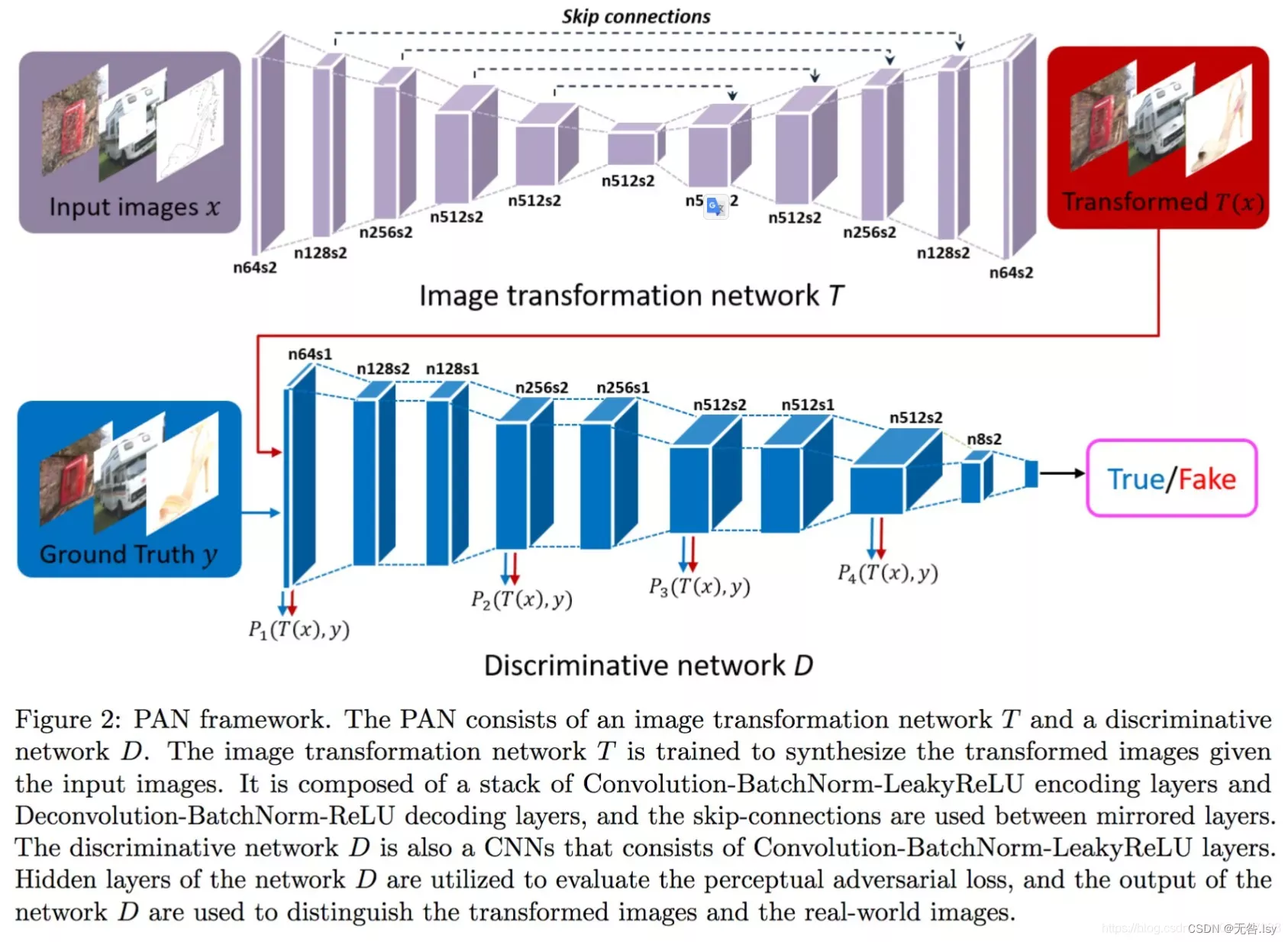
【深度学习】pix2pix GAN理论及代码实现
Cholesterol-PEG-Thiol, CLS-PEG-SH, Cholesterol-PEG-Sulfhydryl for improved solubility

39. 组合总和 && 40. 组合总和2 && 216. 组合总和3
随机推荐
下秒数据:湖仓一体带来的现代数据堆栈变革开始了
Win11找不到Internet Explore怎么办
C语言预处理命令是什么?
没有 accept,我可以建立 TCP 连接吗?
2.2 监督学习-1
Definition and Basic Operations of Sequence Tables
阿里二面:没有 accept,能建立 TCP 连接吗?
顺序表的定义和基本操作
Ali Ermi: Without accept, can a TCP connection be established?
不经意传输协议OT
Error when source install/setup.bash
FET Mosfet Leiditech corresponds to Infineon Infineon
Prometheus Operator 通过additional 添加target
人人都可以DIY的大玩具,宏光MINIEV GAMEBOY产品力强,出行新装备
10个 Istio 流量管理 最常用的例子,你知道几个?
PMP daily practice | didn't lost a 8.9 (including agile + multi-select)
What to do if Windows 11 can't find Internet Explorer
【stack】【queue】【priority_queue】【deque】详解
Week 8 Deep learning for object detection
Week 8 Deep learning for object detection