About teacher Zhou Zhihua 《 machine learning 》 The study notes of this book
Record the learning process
This blog record Chapter14

1 hidden Markov model

Probability graph model （probabilistic graphical model）： A probabilistic model that uses graphs to express the correlation of variables . The most common is Use a node to represent one or a group of random variables , Between nodes Edges represent the probability correlation between variables , namely Variable diagram . The probability graph model can be roughly classified as ：

• Directed acyclic graph （ Directed graph model or Bayesian network ）
• Undirected graph （ Undirected graph model or Markov Network ）

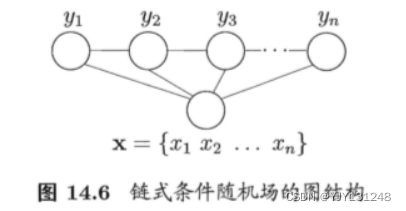
hidden Markov model （HMM）： It's the simplest dynamic Bayesian network , It's a famous digraph model . It is mainly used in time series data modeling . There are two kinds of variables in hidden Markov model ：

• State variables （ Hidden variables ）： It means the first one $i$ System status at any time { y 1 , y 2 , ⋯   , y n } \{y_1,y_2,\cdots,y_n\} { y1​,y2​,⋯,yn​}, It's usually hidden 、 Unobservable .
• Observation variables ： { x 1 , x 2 , ⋯   , x n } \{x_1,x_2,\cdots, x_n\} { x1​,x2​,⋯,xn​}, It means the first one $i$ Observations at the moment .

In hidden Markov model , The system is usually in multiple states { s 1 , s 2 , ⋯   , s N } \{s_1,s_2,\cdots,s_N\} { s1​,s2​,⋯,sN​} Between , So the state variable $y_i$ The value range of is usually $N$ A discrete space with possible values , So the state variable $y_i$ Value range of $Y$ Usually there is $N$ A discrete space with possible values （$Y\subset S$）. The observed variables can be discrete or continuous . For the convenience of discussion , We assume that its value range X = { o 1 , o 2 , ⋯   , o M } X=\{o_1,o_2,\cdots,o_M\} X={ o1​,o2​,⋯,oM​}.

At any moment , The value of the observed variable $x_t$ Only by state variables $y_t$ determine , It has nothing to do with the values of other state variables and observation variables . meanwhile $t$ The state of the moment $y_t$ Only depends on $t-1$ The state of the moment $y_{t-1}$, And the rest $n-2$ It has nothing to do with two states , That's what's called “ Markov chain ”： The next state of the system is determined only by the current state , Not dependent on any previous state . The joint probability distribution of all variables is defined as ：
$$P(x_1,y_1,\cdots ,x_n,y_n)=P(y_1)P(x_1|y_1)\prod _{i=2}^{n}P(y_i|y_{i-1})P(x_i|y_i)$$
In addition to structural information , To determine a hidden Markov model, we also need the following three sets of parameters ：

• State transition probability ：
  $$a_{ij}=P(y_{t+1}=s_j|y_t=s_i),1\le i,j\le N$$

• Output observation probability ：
  $$b_{ij}=P(x_t=o_j|y_t=s_i)$$

• Initial state probability ：
  $${\pi }_i=P(y_1=s_i)$$

---

2 Markov random Airport

Markov random Airport （MRF）： A typical Markov Network , Is a famous undirected graph model :

• node ： A variable or set of variables
• edge ： Dependencies between variables

Markov random fields have a set of potential functions （potential functions）, It's also called “ factor ”, That is, a nonnegative real function defined on a subset of variables , It is mainly used to define the probability distribution function .

In Markov random fields , For a subset of nodes in the graph , If any two nodes have edge connections , The node subset is called a “ group ”, If you add another node to the group , Can't form a group , It is called a “ Great regiment ”.

In Markov random field , The joint probability distribution among multiple variables can be decomposed into the product of multiple factors based on the clique decomposition , Each factor is related to only one cluster . say concretely , about $n$ A variable X = { x 1 , x 2 , ⋯   , x n } X=\{x_1,x_2,\cdots, x_n\} X={ x1​,x2​,⋯,xn​} , The set of all groups is $C$, And regiment $Q\in C$ The corresponding variable set is recorded as $X_Q$ , Then the joint probability $P(X)$ Defined as
$$P(X)=\frac{1}{Z}\prod _{Q\in C}\psi (X_Q)$$
How to get... In Markov random field “ Conditional independence ” Well ？ Also with the help of Separate The concept of . As shown in the figure below , If from the node set A Node in to B All nodes in must pass through the node set C Node in , Then it is called node set A and B Passive node set C Separate , C be called " Separate sets " (separating set).

Yes, Markov random field , Yes “ Global markov ” (global Markov property)： Given the separation set of two variable subsets , Then the two variable subsets are conditionally independent . in other words , In the picture A, B and C The corresponding variable sets are $X_A,X_B,X_C$, be $X_A$ and $X_B$ In the given $X_C$ Under the condition of Independence , Write it down as $XA\perp XB|X_C$.

By global Markov property , Two useful inferences can be drawn ：

• Local Markov ： Given the adjacency of a variable , Then the variable condition is independent of other variables .
• Paired markov sex ： Given all the other variables , Two nonadjacent variables are conditionally independent .

Let's look at the potential function in Markov random field , Its effect is Quantitative characterization of variable sets $X_Q$ Correlation of variables in （ Nonnegative function ）, And There is a preference for the value of all variables .

To satisfy nonnegativity , Exponential functions are often defined as potential functions ：
$${\psi }_Q(X_Q)=e^{-H_Q(X_Q)}$$

3 Conditional random field

Conditional random field (Conditional Random Field, abbreviation CRF) It's a discriminant undirected graph model , It's a discriminant model . Conditional random fields try to deal with multiple variables in Conditional probability after given Observations Modeling .

Make $G=(V,E)$ Represents nodes and marked variables $y$ Undirected graph with one-to-one correspondence of prime ,$y_v$ Indicates the connection with the node $v$ The corresponding tag variable , $n(v)$ Represents a node $v$ Adjacent nodes of , If the figure $G$ Each variable of the $y_v$ All satisfy Markov property , namely
P ( y v ∣ x , y V \ { v } ) = P ( y v ∣ x , y n ( v ) ) P(y_v|x,y_{V\backslash \{v\}})=P(y_v|x,y_{n(v)}) P(yv​∣x,yV\{ v}​)=P(yv​∣x,yn(v)​)
be $(y,x)$ Constitute a conditional random field .

4 Learning and inference

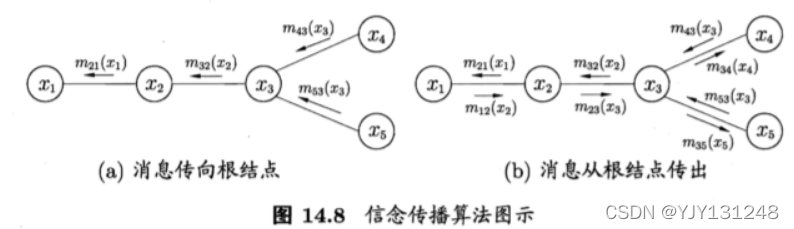
• Variable elimination

• The spread of faith

5 Approximate inference

• MCMC sampling ： The key is to construct " The stationary distribution is $p$ Markov chain of " To generate samples .
• Variational inference ： By using the known simple distribution to approximate the complex distribution to be inferred , And by limiting the type of approximate distribution , Thus, a local optimal 、 But the approximate a posteriori distribution with definite solution .

6 Topic model

Topic model (topic model) It's a family Generative directed graph model , It is mainly used to process discrete data ( Such as text collection ), In information retrieval 、 Natural language processing and other fields are widely used . Implicit Dirichlet distribution model (Latent Dirichlet Allocation, abbreviation LDA) It is a typical representative of topic model .

Basic concepts in topic model ：

• word （word）： The most basic discrete element
• file （document）： Regardless of the order （ The word bag ）
• topic of conversation （topic）： A series of Related words , And the probability of their occurrence under this probability

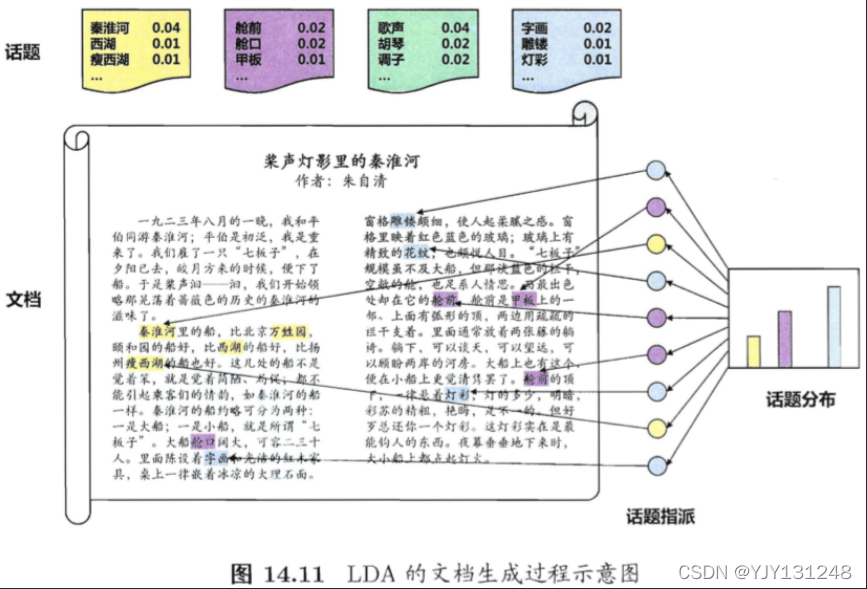
Let's assume that the dataset contains a total of $K$ A topic and $T$ document , The word in the document comes from a containing $N$ A dictionary of words . We use it $T$ individual $N$ Dimension vector w = { w 1 , w 2 , ⋯   , w T } w=\{w_1,w_2,\cdots,w_T\} w={ w1​,w2​,⋯,wT​} Represents a dataset ( Document collection ), $K$ individual $N$ Dimension vector ${\beta }_k(k=1,2,\cdots ,K)$ It means the topic , among $w_T\in {\mathbb{R}}^N$ Of the $n$ Weight $w_{t,n}$ Represents a document $t$ Middle word $n$ The frequency of words ,${\beta }_k\in {\mathbb{R}}^N$ Of the $n$ Weight ${\beta }_{k,n}$ It means the topic $k$ Middle word $n$ The frequency of words .

LDA Look at documents and topics from the perspective of a generative model . say concretely ,LDA Think that each document contains multiple topics , You might as well use vectors ${\theta }_t\in {\mathbb{R}}^N$ Represents a document $t$ The proportion of each topic included in ,${\theta }_{t,k}$ Represents a document $t$ Topics included in $k$ The proportion of , Then through the following steps from the topic " Generate " file $t$：

• According to the parameters $\alpha$ The Dirichlet distribution randomly samples a topic distribution ${\theta }_t$
• Follow the steps below to generate... In the document $N$ Word
  • according to ${\theta }_t$ Assign topics , Get document $t$ Middle word $n$ The topic of $z_{t,n}$
  • According to the word frequency distribution corresponding to the assigned topic ${\beta }_k$ Random sampling generates words