pytorch geometric Why should sparse adjacency matrix be written in the form of transpose adj_t

First contact pytorch geometric My little friend may have the same question as me , Why should the adjacency matrix in data be written in the form of transpose . Until I read the source code , I understand the author's writing , Because of the way information is transmitted , Here I share with you .

edge_index

First pytorch geometric There are two storage modes for edge information , The first is edge_index, its shape yes [2, N], among N Is the number of edges . first N The element of dimension stores the information of the origin of the edge , be called source, the second N The element of dimension stores the information of the target point of the edge , be called target. for instance , If we have such a directed graph , that edge_index That's true : tensor([[1, 2, 3, 4], [0, 0, 0, 0]]), Side is (1,0), (2,0), (3,0), (3,0)

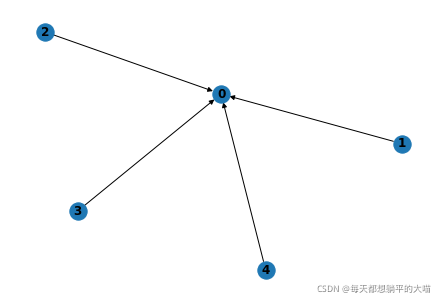
If the graph above is undirected , that 0 This node also points to 1,2,3,4 These nodes ,edge_index It should be : tensor([[1, 2, 3, 4,0, 0, 0, 0], [0, 0, 0, 0, 1, 2, 3, 4]]), Side is (1,0), (2,0), (3,0), (3,0), (0,1), (0,2), (0,3), (0,4).
edge_index The reason for this is , stay pytorch geometric in , use scatter A kind of method can be easily realized , from source To target, This default edge transfer method .（ Of course, you can also change the transmission mode from target Pass on to source.） If you still don't understand the above , Then remember , The way of edge transfer is from source To target Of , Later, in the process of looking at the source code , It will come to understand .

adj_t

pytorch geometric The second storage mode of edge information is adj_t, It's a sparse tensor. Here we see the author in adj Add... To the back t, It shows that it is the transpose of adjacency matrix . Why write it as transpose , Let's go up edge_index speak .
First, why do we need sparse adjacency matrix , Not directly edge_index？ That's because if sparse adjacency matrix can be used, the computing speed can be greatly accelerated , To save memory . Of course, we also have some graph algorithms that cannot avoid explicit edge passing , such as GAT This kind of graph algorithm that needs to operate alone on the edge .
take edge_index When converting to adjacency matrix , Naturally, I will write the following form ：

adj = SparseTensor(row=edge_index[0], col=edge_index[1], value=...,
                   sparse_sizes=(num_nodes, num_nodes))

But we all know that , Matrix computing AW It is the process of aggregating the characteristics of neighbors on a row , among A It's an adjacency matrix ,W Is the characteristic matrix . If it is just a small partner of the contact graph algorithm , I borrowed the following picture , You can see it , Each node finally generates embedding It's in A Sum of eigenvalues corresponding to neighbors in the row , therefore In essence, it aggregates the information corresponding to the column to the row . In the figure A Only neighbors E, But think about it D, It has B, C, E Three neighbors , So its characteristic is B, C, E Sum of three neighbor characteristics , Aggregate the columns B, C, E Corresponding information to... In the line D.

So there's a problem ,edge_index Information transmission in is source to target, That is to say edge_index[0] to edge_index[1], and adj Medium is col To row, This creates a problem of inconsistency . So when doing matrix calculation and transmitting information , The author will adj convert to adj_t, And make it the default form , This is consistent .

give an example

Look at an author's document about GIN Examples of implementations ：https://pytorch-geometric.readthedocs.io/en/latest/notes/sparse_tensor.html?highlight=adj_t#memory-efficient-aggregations

from torch_sparse import matmul

class GINConv(MessagePassing):
    def __init__(self):
        super().__init__(aggr="add")

    def forward(self, x, edge_index):
        out = self.propagate(edge_index, x=x)
        return MLP((1 + eps) x + out)

    def message(self, x_j):
        return x_j

    def message_and_aggregate(self, adj_t, x):
        return matmul(adj_t, x, reduce=self.aggr)

You can see in the message_and_aggregate This step is in the process of information transmission , Default is used adj_t.

I'm talking to the new pytorch geometric Series of tutorials pytorch_geometric Code details , Welcome to comment and exchange .