当前位置:网站首页>数论知识点
数论知识点
2022-08-09 11:03:00 【Rachel caramel】
1.快速幂
2^10
= 4^5
=4*16^2
= 4 *256
eg.求a^b
int power(int a,int b)
{
int res=1;
while(b)
{
if(b&1) res*=a;
b>>=1;
a=a*a;
}
return res;
}
某些时候可能需要进行强制类型转换模板例题
2.
a=4*a;//等价于a<<=2
a*=10;//等价于(a<<3)+(a<<1)
a*=15;//等价于(a<<4)-a
11111(30个1)等价于(1<<31)-1
//a,b交换位置
a^=b^=a^=b;
4.杨辉三角与排列组合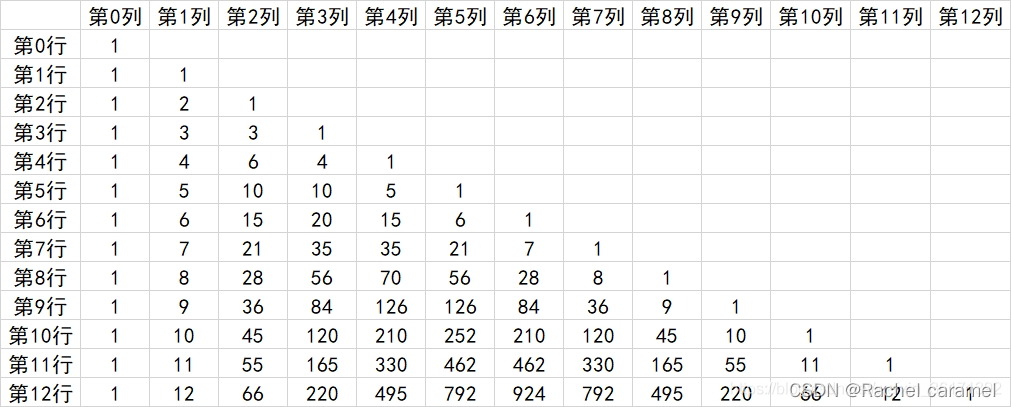
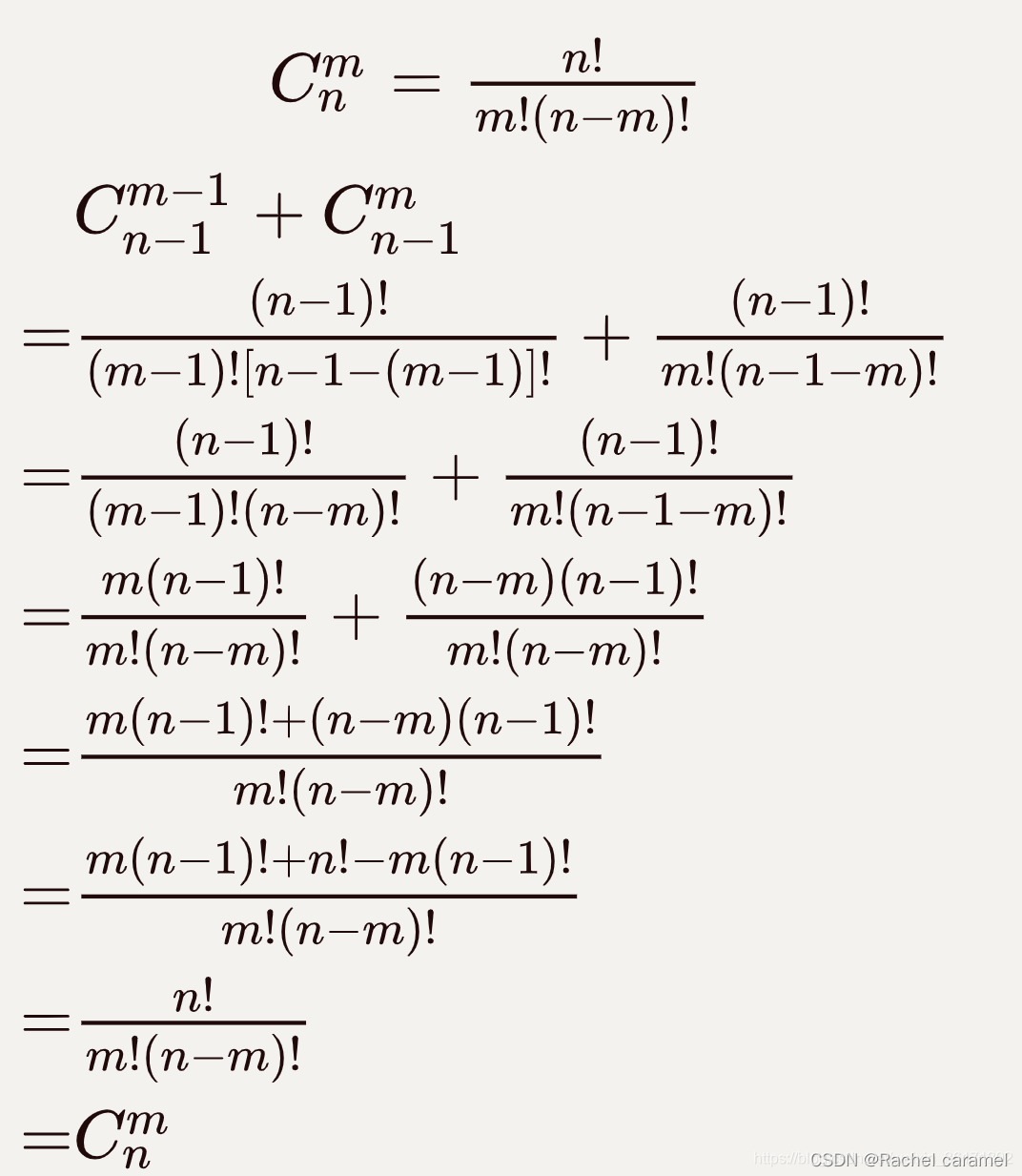
5.质数筛
最普通的判定 O(n*n^(1/2))
int prime[maxn];
int cnt=0;
prime[++cnt]=2;
prime[++cnt]=3;
for(int i=4;i<=n;i++)
{
int flag=1;
for(int j=2;j*j<=4;j++)
{
if(i%j==0)
{
flag=0;
break;
}
}
if(flag) prime[++cnt]=i;
}
垃圾筛(埃拉托斯特尼筛法)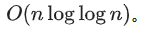
bool isprime[maxn];
int prime[maxn];
int cnt=0;
int getprime(int n)
{
for(int i=1;i<=n;i++) isprime[i]=1;
isprime[1]=0;
for(int i=2;i<=n;i++)
{
if(isprime[i])
{
prime[++cnt]=i;
if((long long)i*i<n)
{
for(int j=i*i;j<=n;j+=i) isprime[j]=0;
}
}
}
rertun cnt;
}
线性筛(欧拉筛)
void getprime()
{
for(int i=2;i<=n;i++)
{
if (!notprime[i]) prime[++tot]=i;
for (int j=1;j<=tot&&i*prime[j]<=n;j++)
{
notprime[i*prime[j]]=1;
if (i%prime[j]==0) break;
}
}
}
理解:
if (i%prime[j]==0) break;
text{这一句是关键,如果i=4的话,当prime[j]=2时,标记8不是素数,然后就跳出了循环
如果此时不跳出循环,12将会在这个时候被筛掉,但
4 ⋅ 3 = 6 ⋅ 2 = 12 4\cdot 3=6\cdot 2=12 4⋅3=6⋅2=12
实际上12应该被2筛掉,也就是被他的最小素数筛掉,因此当i是prime[j]的倍数时应该直接跳出循环
6.
^可以看成+(简便记法
1^1=0 1+1=10=0
1^0=1 1+0=0
0^0=0 0+0=0
7.
例题
gcd (grand common divisor,即最大公约数)
(a,b)即求a和b的最大公约数
(a,b)=(b,b%a)
证明:
a = k 1 ⋅ c b = k 2 ⋅ c a=k_1\cdot c\\ b=k_2\cdot c a=k1⋅cb=k2⋅c
即(a,b)=( k 1 ⋅ c , b = k 2 ⋅ c k_1\cdot c,b=k_2\cdot c k1⋅c,b=k2⋅c)
所以( k 1 , k 2 k_1,k_2 k1,k2)=1
b = k 2 ⋅ c = k 3 ⋅ d a m o d b = ( k 1 , k 2 ) ⋅ c = c b=k_2\cdot c=k_3\cdot d\\ a\bmod b =(k_1,k_2)\cdot c=c b=k2⋅c=k3⋅damodb=(k1,k2)⋅c=c
int gcd(int a,int b)
{
if (!b) return a;
return gcd(b,a%b);
}
int gcd(int a,int b)
{
while (b)
{
int t=b;
b=a%b;
a=t;
}
return a;
}
#include <algorithm>
__gcd(x,y);
9.还需理解
逆元
eg.
3*4=1(mod11)
这里4是3的逆元,相当于1/3
oiwiki的逆元讲解
边栏推荐
猜你喜欢
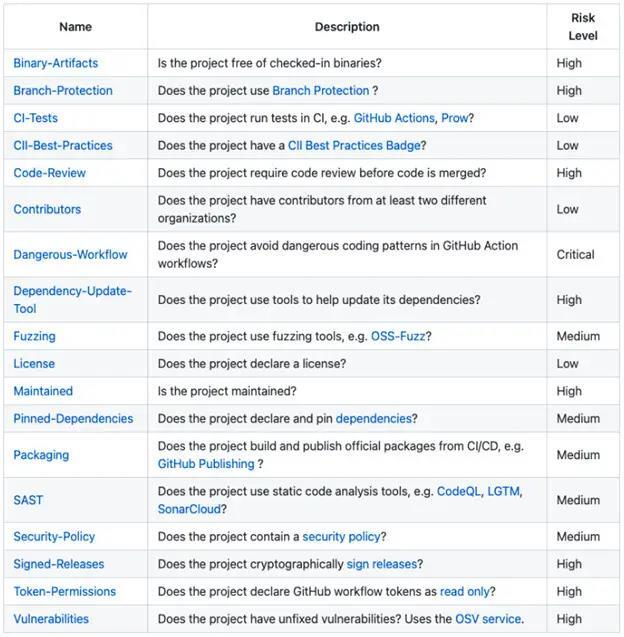
OpenSSF's open source software risk assessment tool: Scorecards
Tensorflow realize parameter adjustment of linear equations
electron 应用开发优秀实践
MDK添加注释模板

wait系统调用
多商户商城系统功能拆解26讲-平台端分销设置
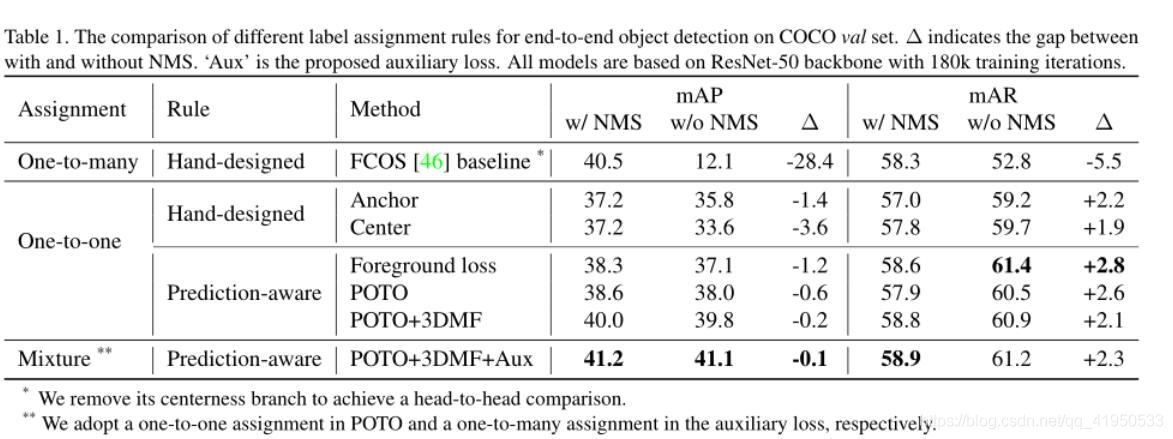
End-to-End Object Detection with Fully Convolutional Network学习笔记

tensorflow实现线性方程的参数调整
CentOS6.5 32bit安装Oracle-11gR2步骤说明

去除蜂窝状的噪声(matlab实现)
随机推荐
torch.cat()函数的官方解释,详解以及例子
sublime记录
activemq message persistence
WebSocket
Preparation for gold three silver four: how to successfully get an Ali offer (experience + interview questions + how to prepare)
美的数字化平台 iBUILDING 背后的技术选型
Qt 国际化翻译
C语言数组题_校门外的树_标记法
无刷无霍尔BLCD电机控制
商业技术解决方案与高阶技术专题 - 数据可视化专题
ACM最长不下降子序列问题
matlab fcnchk 函数用法
激光条纹中心提取——Steger
实测办公场景下,国产远程控制软件的表现力如何?(技术解析)
STM32使用静态队列保存数据
Open3D 点云平均点间距评估
性能测试(04)-表达式和业务关联-JDBC关联
Qt获取EXE可执行文件的上一级目录下的文件
Looper 原理浅析
ThreadLocal及其内存泄露分析