当前位置:网站首页>LeetCode 练习——396. 旋转函数
LeetCode 练习——396. 旋转函数
2022-04-23 14:48:00 【SK_Jaco】
1.题目描述
给定一个长度为 n 的整数数组 nums 。
假设 arrk 是数组 nums 顺时针旋转 k 个位置后的数组,我们定义 nums 的 旋转函数 F 为:
F(k) = 0 * arrk[0] + 1 * arrk[1] + … + (n - 1) * arrk[n - 1]
返回 F(0), F(1), …, F(n-1)中的最大值 。
生成的测试用例让答案符合 32 位 整数。
示例 1:
输入: nums = [4,3,2,6]
输出: 26
解释:
F(0) = (0 * 4) + (1 * 3) + (2 * 2) + (3 * 6) = 0 + 3 + 4 + 18 = 25
F(1) = (0 * 6) + (1 * 4) + (2 * 3) + (3 * 2) = 0 + 4 + 6 + 6 = 16
F(2) = (0 * 2) + (1 * 6) + (2 * 4) + (3 * 3) = 0 + 6 + 8 + 9 = 23
F(3) = (0 * 3) + (1 * 2) + (2 * 6) + (3 * 4) = 0 + 2 + 12 + 12 = 26
所以 F(0), F(1), F(2), F(3) 中的最大值是 F(3) = 26 。
示例 2:
输入: nums = [100]
输出: 0
2.思路
2.1 代码
这道题挺有趣,如果使用暴力循环会提示超时,因此需要对公式进行分析。以题目示例进行分析,
进一步观察推导,在每一步中补上一个元素可以得到整个数组的和,即
F ( 0 ) = 0 ∗ n u m s [ 0 ] + 1 ∗ n u m s [ 1 ] + 2 ∗ n u m s [ 2 ] + 3 ∗ n u m s [ 3 ] F ( 1 ) = 0 ∗ n u m s [ 3 ] + 1 ∗ n u m s [ 0 ] + 2 ∗ n u m s [ 1 ] + 3 ∗ n u m s [ 2 ] = F ( 0 ) + n u m s [ 0 ] + n u m s [ 1 ] + n u m s [ 2 ] − 3 ∗ n u m s [ 3 ] = F ( 0 ) + ( n u m s [ 0 ] + n u m s [ 1 ] + n u m s [ 2 ] + n u m s [ 3 ] ) − 4 ∗ n u m s [ 3 ] F ( 2 ) = 0 ∗ n u m s [ 2 ] + 1 ∗ n u m s [ 3 ] + 2 ∗ n u m s [ 0 ] + 3 ∗ n u m s [ 1 ] = F ( 1 ) + n u m [ 0 ] + n u m [ 1 ] + n u m [ 3 ] − 3 ∗ n u m [ 2 ] = F ( 1 ) + ( n u m [ 0 ] + n u m s [ 2 ] + n u m [ 1 ] + n u m [ 3 ] ) − 4 ∗ n u m [ 2 F ( 3 ) = 0 ∗ n u m s [ 1 ] + 1 ∗ n u m s [ 2 ] + 2 ∗ n u m s [ 3 ] + 3 ∗ n u m s [ 0 ] = F ( 2 ) + n u m [ 1 ] + n u m [ 2 ] + n u m [ 3 ] − 3 ∗ n u m [ 0 = F ( 2 ) + ( n u m s [ 0 ] + n u m [ 1 ] + n u m [ 2 ] + n u m [ 3 ] ) − 4 ∗ n u m [ 0 ] \begin{aligned} F(0)&=0*nums[0]+1*nums[1]+2*nums[2]+3*nums[3]\\ \\ F(1)&=0*nums[3]+1*nums[0]+2*nums[1]+3*nums[2]\\ &=F(0)+nums[0]+nums[1]+nums[2]-3*nums[3]\\ &=F(0)+(nums[0]+nums[1]+nums[2]+nums[3])-4*nums[3]\\ \\ F(2)&=0*nums[2]+1*nums[3]+2*nums[0]+3*nums[1]\\ &=F(1)+num[0]+num[1]+num[3]-3*num[2]\\ &=F(1)+(num[0]+nums[2]+num[1]+num[3])-4*num[2\\ \\ F(3)&=0*nums[1]+1*nums[2]+2*nums[3]+3*nums[0]\\ &=F(2)+num[1]+num[2]+num[3]-3*num[0\\ &=F(2)+(nums[0]+num[1]+num[2]+num[3])-4*num[0]\\ \end{aligned} F(0)F(1)F(2)F(3)=0∗nums[0]+1∗nums[1]+2∗nums[2]+3∗nums[3]=0∗nums[3]+1∗nums[0]+2∗nums[1]+3∗nums[2]=F(0)+nums[0]+nums[1]+nums[2]−3∗nums[3]=F(0)+(nums[0]+nums[1]+nums[2]+nums[3])−4∗nums[3]=0∗nums[2]+1∗nums[3]+2∗nums[0]+3∗nums[1]=F(1)+num[0]+num[1]+num[3]−3∗num[2]=F(1)+(num[0]+nums[2]+num[1]+num[3])−4∗num[2=0∗nums[1]+1∗nums[2]+2∗nums[3]+3∗nums[0]=F(2)+num[1]+num[2]+num[3]−3∗num[0=F(2)+(nums[0]+num[1]+num[2]+num[3])−4∗num[0]
因此得到推导公式,其中 i 为公式中待减去的角标
F i ( n ) = F i ( n − 1 ) + ∑ i = 0 n n u m s − n u m s . L e n g t h ∗ n u m s [ i ] F_{i}(n)=F_{i}(n-1)+ \sum_{i=0}^n nums-nums.Length*nums[i] Fi(n)=Fi(n−1)+i=0∑nnums−nums.Length∗nums[i]
代码如下:
class Solution {
public int maxRotateFunction(int[] nums) {
int sum = 0;
int max = Integer.MIN_VALUE;
int curr = 0;
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
curr += nums[i] * i;
}
max = Math.max(max,curr);
for (int i = nums.length - 1; i > 0; i--) {
curr += sum - nums.length * nums[i];
max = Math.max(max,curr);
}
return max;
}
}
2.2 测试结果
通过测试

3.总结
- 暴力循环解决会超时
- 观察示例进行公式推导即可
版权声明
本文为[SK_Jaco]所创,转载请带上原文链接,感谢
https://blog.csdn.net/qq_38550836/article/details/124342109
边栏推荐
- MDS55-16-ASEMI整流模块MDS55-16
- [detailed explanation of factory mode] factory method mode
- UML project example -- UML diagram description of tiktok
- Multisim Simulation Design of DC adjustable regulated power supply of LM317 (with simulation + paper + reference)
- Design of single chip microcomputer Proteus for temperature and humidity monitoring and alarm system of SHT11 sensor (with simulation + paper + program, etc.)
- What is the main purpose of PCIe X1 slot?
- We reference My97DatePicker to realize the use of time plug-in
- [jz46 translate numbers into strings]
- SHT11传感器的温度湿度监控报警系统单片机Proteus设计(附仿真+论文+程序等)
- async void 导致程序崩溃
猜你喜欢
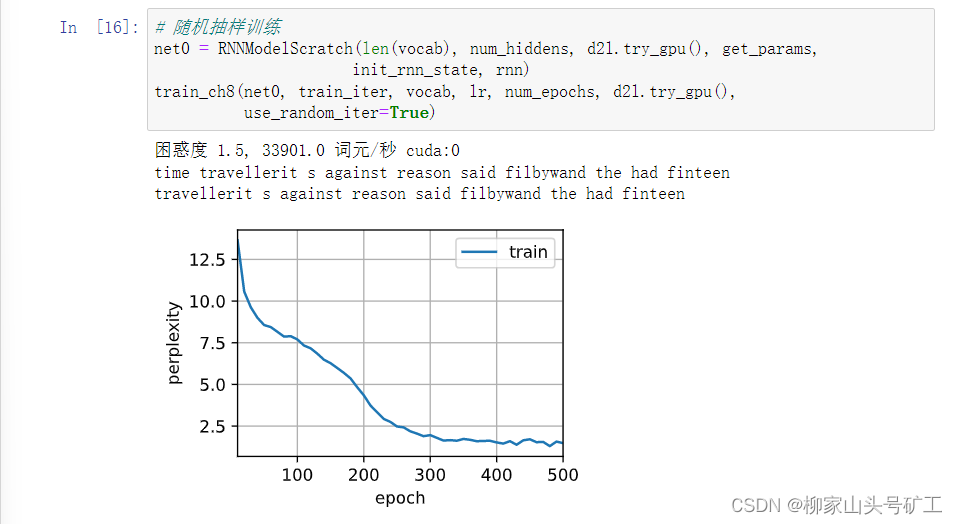
8.4 循环神经网络从零实现
SHT11传感器的温度湿度监控报警系统单片机Proteus设计(附仿真+论文+程序等)
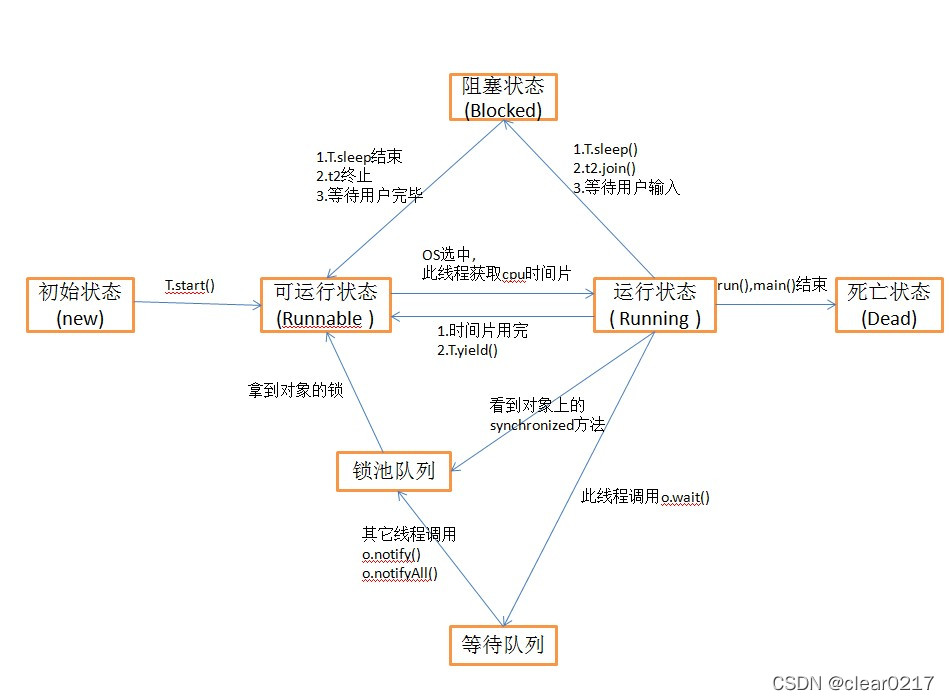
Thread synchronization, life cycle
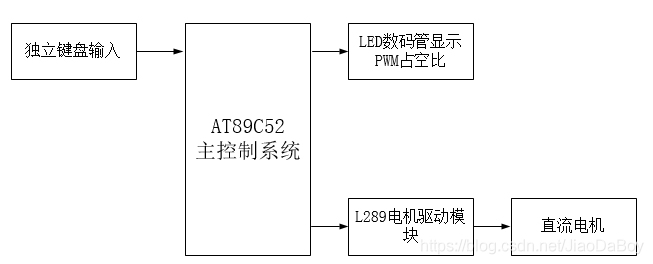
PWM speed regulation control system of DC motor based on 51 single chip microcomputer (with complete set of data such as Proteus simulation + C program)
51 Single Chip Microcomputer Design of traffic light system (with Proteus simulation, C program, schematic diagram, PCB, thesis and other complete data)

交通灯系统51单片机设计(附Proteus仿真、C程序、原理图及PCB、论文等全套资料)
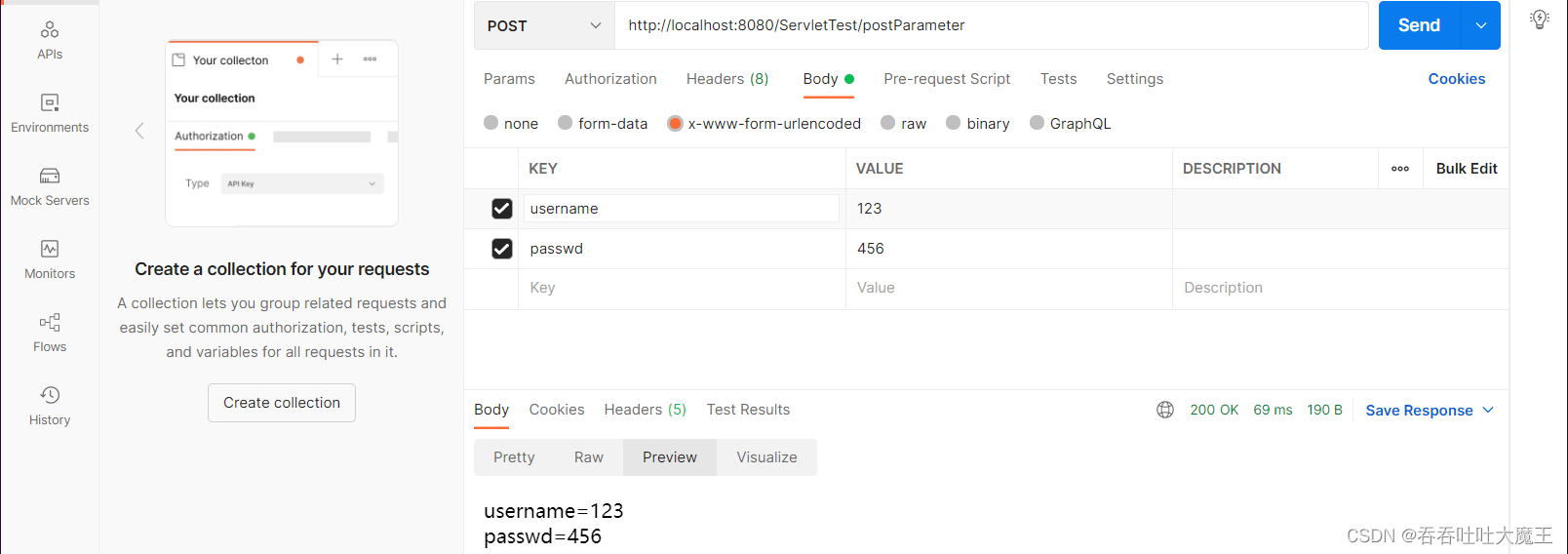
【Servlet】Servlet 详解(使用+原理)
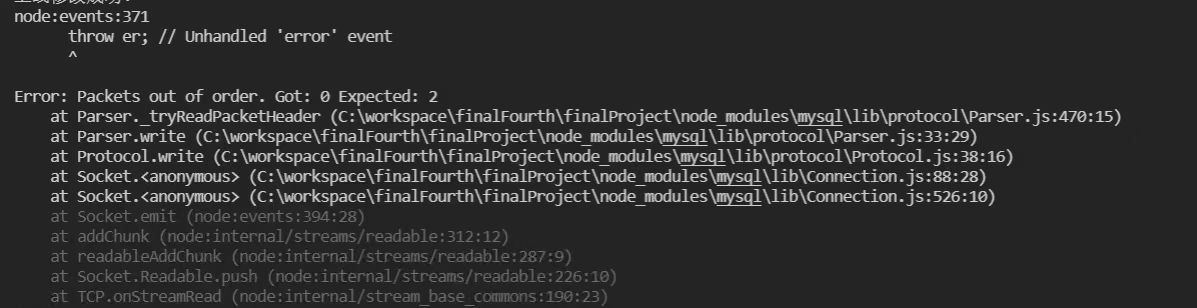
MySQL报错packet out of order
![[NLP] HMM hidden Markov + Viterbi word segmentation](/img/9a/b39a166320c2f2001f10913f789c90.png)
[NLP] HMM hidden Markov + Viterbi word segmentation
8.5 循环神经网络简洁实现
随机推荐
QT interface optimization: QT border removal and form rounding
One of the advanced applications of I / O reuse: non blocking connect -- implemented using select (or poll)
线程同步、生命周期
Matlab Simulink modeling and design of single-phase AC-AC frequency converter, with MATLAB simulation, PPT and papers
压缩映射定理
三、梯度下降求解最小θ
Multisim Simulation Design of DC adjustable regulated power supply of LM317 (with simulation + paper + reference)
TLC5615 based multi-channel adjustable CNC DC regulated power supply, 51 single chip microcomputer, including proteus simulation and C code
你还不知道责任链模式的使用场景吗?
你還不知道責任鏈模式的使用場景嗎?
电容
全连接层的作用是什么?
Detailed explanation of C language P2 selection branch statement
[proteus simulation] automatic range (range < 10V) switching digital voltmeter
Vous ne connaissez pas encore les scénarios d'utilisation du modèle de chaîne de responsabilité?
Swift Protocol 关联对象 资源名称管理 多线程GCD 延迟 once
Set up an AI team in the game world and start the super parametric multi-agent "chaos fight"
capacitance
go基础 反射
[NLP] HMM hidden Markov + Viterbi word segmentation