2019.02.19 Update for convenience and simplicity, remember FFT, Sum up two paragraphs to record

1024 spot FFT Medium 1024 It refers to the number of input real numbers , however FFT The input is usually a complex number , That is to say 1024 Plural .FFT The output is 1024 Plural , Only before calculation 512 Plural

summary

N spot FFT Medium N It refers to the number of input real numbers , however FFT The input of a function is usually a complex number , That is to say N Plural .FFT The output is N Plural , Only before calculation N/2 Plural

 

 

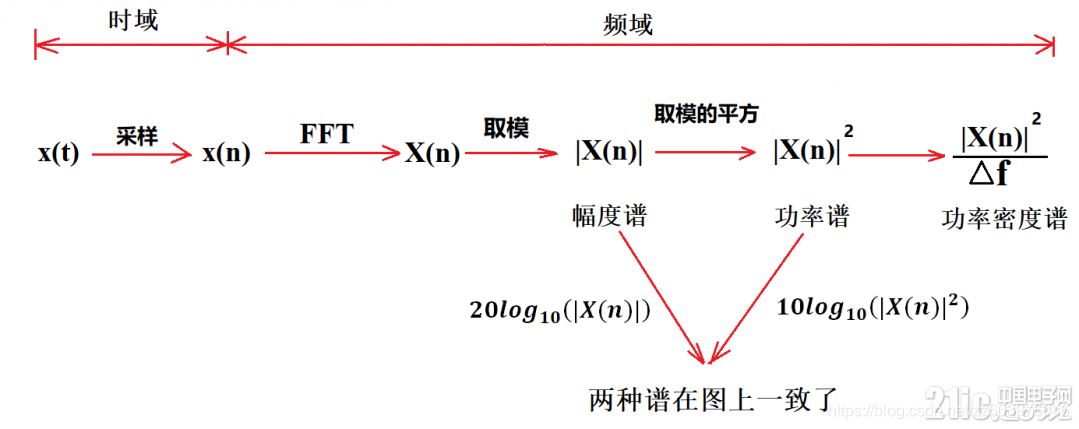
① FFT The physical meaning of the results

FFT Physical meaning

FFT It's a fast algorithm for DFT , A signal can be transformed  
To the frequency domain . So as to analyze the frequency domain characteristics of the signal . Commonly used in spectrum analysis .

The time domain signal passes directly through ADC Sample to obtain .

Sampling points

• The sampling frequency is more than twice the signal frequency
• N A sampling point , after FFT after , You can get N Point FFT result . For convenience FFT operation , Usually N take 2 Integer power of .

The significance of the results

• The number of sampling points is N. that FFT And the result is a N Some of the plural . Every point corresponds to a frequency point .
• Suppose the peak value of the original signal is A, that FFT Every point of the result （ Except for the DC component of the first point ） The modulus of is A Of N/2 times . And the first point is the DC component , Its modulus is the DC component N times .
• Frequency points correspond to FFT As a result, the phase of the signal under the included angle of the complex number .
• The first point represents the DC component （ namely 0Hz）, And the last point N The next point of （ Actually this point doesn't exist , Here is the hypothetical number N + 1 A little bit , It can also be seen as dividing the first point into two halves , The other half moves to the end ） It means the sampling frequency Fs, In the middle was N - 1 Divide the points equally N Equal parts , The frequency of each point increases in turn . For example, at some point n The frequency is ：Fn = (n - 1) * Fs / N.Fn It can be distinguished that the frequency is Fs/N, If the sampling frequency Fs by 1024Hz, The number of sampling points is 1024 spot , You can tell 1Hz, Each point is 1Hz. be aware 0Hz Is the first point, not the coordinate origin If you want to improve the frequency resolution , The number of sampling points must be increased , That is, the sampling time . Frequency resolution and sampling time are reciprocal . To improve the frequency resolution , You need to increase the number of sampling points , This is unrealistic in some practical applications , The analysis needs to be completed in a short time . The way to solve this problem is frequency subdivision , The simpler way is to sample the signal with shorter time , Then add a certain amount of 0, Make its length reach the required number of points , Do it again FFT, This can improve the frequency resolution to a certain extent . The specific frequency subdivision method can refer to the relevant literature .

summary

hypothesis FFT And then something n In the plural a+bi Express , So the module of the complex number is An= Radical sign a*a+b*b, Phase is Pn=atan2(b,a), Range from -pi To pi. Based on the above results , You can figure it out n The expression of the signal corresponding to the point is ：

n = 1
    A1 / N

n ≠ 1, And n <= N / 2
    An / (N / 2) * cos(2 * pi * Fn * t + Pn)
 namely 
    2 * An / N * cos(2 * pi * Fn * t + Pn).

•  

example

expression

S = 2                                           // ①
  + 3.0 * cos(2 * pi * 50 * t - pi * 30 / 180)  // ②
  + 1.5 * cos(2 * pi * 75 * t + pi * 90 / 180)  // ③

The signal ① 2V The DC component of  
The signal ②  frequency 50Hz、 phase -30 degree 、 Range 3.0V The AC signal of  
The signal ③  frequency 75Hz、 phase +90 degree 、 Range 1.5V The AC signal of

sampling

sampling frequency  256Hz 
Number of sampling points  256 spot

according to Fn = (n - 1) * Fs / N, The first n The frequency of a point is n - 1. It can be known that the three signals are on the 1 A little bit 、 The first 51 A little bit 、 The first 76 There are peaks at points . Other points should be close to 0.

FFT Calculation

1 spot ： 512         + 0i
2 spot ： -2.6195E-14 - 1.4162E-13i 
3 spot ： -2.8586E-14 - 1.1898E-13i

50 spot ：-6.2076E-13 - 2.1713E-12i
51 spot ：332.55      - 192i
52 spot ：-1.6707E-12 - 1.5241E-12i

75 spot ：-2.2199E-13 - 1.0076E-12i
76 spot ：3.4315E-12  + 192i
77 spot ：-3.0263E-14 + 7.5609E-13i

Calculate the amplitude

according to An= Radical sign a*a+b*b Calculate the modulus

 1 spot ： 512 =  Radical sign (512 * 512 + 0 * 0)
51 spot ： 384 =  Radical sign (332.55 * 332.55 + 192 * 192)
76 spot ： 192 =  Radical sign ((3.4315E-12) * 3.4315E-12) + 192 * 192)

according to

n = 1
    A1 / N

n ≠ 1, And n <= N / 2
    An / (N / 2) * cos(2 * pi * Fn * t + Pn)
 namely 
    2 * An / N * cos(2 * pi * Fn * t + Pn).

You can calculate the amplitude

 1 spot ： 2.0 = A1 / N       = 512 / 256
51 spot ： 3.0 = An / (N / 2) = 384 / ( 256 / 2)
76 spot ： 1.5 = An / (N / 2) = 192 / ( 256 / 2)

Calculate the phase

according to Pn=atan2(b,a) Calculate radian phase

 1 spot ：  The DC component has no phase 
51 spot ： atan2(-192, 332.55)    = -0.5236
76 spot ： atan2(192, 3.4315E-12) = 1.5708

Convert to angle

51 spot ： 180 * (-0.5236) / pi = -30.0001
76 spot ： 180 * (1.57080) / pi = +90.0002

Reference article Matlab routine

close all;        % Close all pictures first 
Adc=2;            % DC component amplitude 
A1=3;             % frequency F1 Signal amplitude 
A2=1.5;           % frequency F2 Signal amplitude 
F1=50;            % The signal 1 frequency (Hz)
F2=75;            % The signal 2 frequency (Hz)
Fs=256;           % sampling frequency (Hz)
P1=-30;           % The signal 1 phase ( degree )
P2=90;            % Signal phase ( degree )
N=256;            % Number of sampling points 
t=[0:1/Fs:N/Fs];  % Sampling time 

% The signal 
S=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180);

% Display the original signal 
plot(S);
title('signal');

figure;
Y = fft(S,N);                 % do FFT Transformation 
Ayy = (abs(Y));               % modulus 
plot(Ayy(1:N));               % Show original FFT Modulus results 
title('Frequency spectrum');

figure;
Ayy=Ayy/(N/2);                % Convert to actual amplitude 
Ayy(1)=Ayy(1)/2;
F=([1:N]-1)*Fs/N;             % Convert to actual frequency value 
plot(F(1:N/2),Ayy(1:N/2));    % Displays the converted FFT Modulus results 
title('Amplitude-frequency');

figure;
Pyy=[1:N/2];
for i=1:N/2
 Pyy(i)=phase(Y(i));          % Calculate the phase 
 Pyy(i)=Pyy(i)*180/pi;        % Convert to angle 
end;
plot(F(1:N/2),Pyy(1:N/2));    % Display phase diagram 
title('Phase, frequency');

personal Matlab routine

To be completed

Freq  = 1000;
Fs    = 44100;
N     = 44100;

t = linspace(0, 1, N);
x = sin(2 * pi * Freq * t);
y = fft(x);

subplot(2, 2, 1);
Crycle3N = ((3 / Freq) * Fs) + 1;
plot(1000 * t(1 : Crycle3N), x(1 : Crycle3N), "LineWidth", 3);
grid;
title('Frequency spectrum');
xlabel("Time in milliseconds");
ylabel("Signal amplitude");

subplot(2, 2, 2);
plot(abs(y(1 : (N / 2))), "LineWidth", 3);
grid;
xlabel("Frequency");
ylabel("Signal amplitude");