当前位置:网站首页>Less than 100 secrets about prime numbers
Less than 100 secrets about prime numbers
2022-04-23 09:41:00 【Zimba_】
Preface :
Delayed for a day , It feels too Nice 了 . So I wrote this blog with difficulty when I almost planned to break the watch .
Because the author becomes lazy , I didn't study hard today , So there's no Euler sieve board , There is no board for prime test , There is no board with large number decomposition . But I try to mention them all . Find your own board , Or write it later and then add .
If the author encounters an unexpected change , Readers don't know what to learn , Please play the game carefully , Enjoy life .
The test of prime numbers :
First, let's talk about what prime numbers are
Now let's introduce how to test prime numbers , According to the author's learning order .
First , The first people to know should be simple o ( n ) o(\sqrt{n}) o(n) Trial division of .( This is not hard to , Let's not talk about the principle )
bool isPrime(ll n)
{
if(n==1)return false;
for(ll i=2;i*i<=n;i++)if(n%i==0)return false;
return true;
}
later , Namely o ( n l o g n ) o(nlogn) o(nlogn) Ehrlich sieve method , It's OK after screening o ( 1 ) o(1) o(1) test .( It's not hard , Let's not talk about the principle )
notPrime[1]=1;
for(ll i=1;i<=n;i++)if(!notPrime[i])
{
for(ll j=2*i;j<=n;j+=i)notPrime[j]=1;
}
This screening method also has Another use , For example, judgment [ a , b ] [a,b] [a,b] The prime number in , among 1 < a < b < 1 e 9 1<a<b<1e9 1<a<b<1e9 And b − a < 1 e 5 b-a<1e5 b−a<1e5. here , We can sift out b \sqrt{b} b All prime numbers in the range , Then take these prime numbers and sift this interval , You can get the answer .
later , Namely o ( n ) o(n) o(n) The Eulerian sieve , After screening, you can o ( 1 ) o(1) o(1) test .
Ashamed to speak , The author can't tear the Euler sieve by hand , Plus I didn't study hard today .
Due to strong copyright awareness , The author didn't go anywhere else to pull the board and put it here .
When the area function is sieved, fill in .
This is a hidden poem .
And finally M i l l e r R a b i n Miller Rabin MillerRabin Prime test of , stay long long It's also very useful in the range . This is a random algorithm , Carry out multiple inspections , The probability of each test being correct is about 1 4 \frac{1}{4} 41, The more inspection times, the more accurate , The complexity is o ( t × l o g n ) o(t\times logn) o(t×logn), among t t t Is the number of inspections .
But after all, it's a random algorithm , With enough complexity , Single inspection still considers o ( n ) o(\sqrt{n}) o(n) Your trial division is better .
Let's talk a little about the principle .
Let's start with the simple Fermat prime test .
according to Fermat's small Theorem : When p p p As a prime number , And g c d ( a , p ) = 1 gcd(a,p)=1 gcd(a,p)=1 when , a p − 1 ≡ 1 ( m o d p ) a^{p-1}\equiv 1(mod\;p) ap−1≡1(modp).
that , If we want to judge the number p p p Don't meet this condition , Then it must not be prime .
But just based on this, there are big loopholes , Because Fermat's theorem is not a necessary and sufficient condition , Sufficiency holds , But the necessity is not tenable .
Some numbers satisfy sufficient conditions , Without meeting the necessary conditions , This is it. Fermat pseudo prime number .
Because of their existence , This makes this test method a big problem .
But the Fermat prime test can score most of the scores . Then we need to find another detection method to further judge .
So we use Second detection : if p p p As a prime number , Then the equation x 2 ≡ 1 ( m o d p ) x^{2}\equiv 1(mod\;p) x2≡1(modp) The solution of is x = 1 x=1 x=1 or x = p − 1 x=p-1 x=p−1.
So how to use it , The key part is coming , Let's start by listing a few things we need to do .
- We want a random number a a a.
- Use a a a Fermat test , have a look a p − 1 ≡ 1 ( m o d p ) a^{p-1}\equiv 1(mod\;p) ap−1≡1(modp) Is it true .
- Then we have to make a second detection , But solving the equation is troublesome , But now we have a p − 1 ≡ 1 ( m o d p ) a^{p-1}\equiv 1(mod\;p) ap−1≡1(modp), So we just need to see a p − 1 2 a^{\frac{p-1}{2}} a2p−1 Is it 1 1 1 or p − 1 p-1 p−1 Just fine .
Come here , We found out , Take the Fermat prime test quickly , And the fast power uses a p − 1 2 a^{\frac{p-1}{2}} a2p−1 Such things .
Then you can write it together .
And when the a p − 1 2 a^{\frac{p-1}{2}} a2p−1 yes 1 1 1 when , You can use him for a second detection ; On the contrary, if it is p − 1 p-1 p−1 Can't continue to use .
So the subcode can be written .
My country and I A moment cannot be divided
Wherever I go A song of praise came out
I sing about every mountain I sing about every river
Smoke from the Little village There is a rut in the road
My dear motherland I will always cling to your heart
You tell me with your mother's warmth
My country and I Like a sea and a spray
Waves are the sons of the sea The sea is the support of that wave
Whenever the sea smiles I am the vortex of laughter
I share the sorrow of the sea Share the joy of the sea
My dear motherland You are the sea that never dries up
Always give me Clear waves The song in my heart
La …… La ……
Always give me Clear waves The song in my heart
that , The test method of prime number is introduced .
Factorization :
First , It's tradition o ( n ) o(\sqrt{n}) o(n) Decomposition of , I don't think I can write anymore .
Then the same as the prime test Strange sex skill , Large number decomposition .
Complexity can achieve o ( n 0.25 ) o(n^{0.25}) o(n0.25), But like the prime test, it's a random algorithm , So it's not very stable , Unless you have to , Otherwise, use less . I haven't seen the principle yet , Don't write .
The code is as follows :
As for the code , As you can see now , There is no such thing , But there are still a lot of online boards .
Prime density :
Also known as the prime distribution theorem . That is to say , Two adjacent prime numbers are not too far apart , Is probably o ( l o g 2 n ) o(log^{2}n) o(log2n) Grade . 1 e 9 1e9 1e9 The maximum spacing in the range is 300 300 300 Small ( Or perhaps 250 250 250?).( 1 e 18 1e18 1e18 It doesn't seem to exceed 500 500 500?)
Specific applications can be seen many times , For example, let you ask less than n ( 2 < n < 1 e 9 ) n(2<n<1e9) n(2<n<1e9) The maximum prime number of , With this theorem , You can judge .
版权声明
本文为[Zimba_]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204230621425578.html
边栏推荐
- Installation of data cleaning ETL tool kettle
- Kernel PWN learning (4) -- double fetch & 0ctf2018 baby
- Employee probation application (Luzhou Laojiao)
- Cloud computing competition -- basic part of 2020 competition [task 3]
- SAP ECC connecting SAP pi system configuration
- Leetcode题库78. 子集(递归 c实现)
- Kettle experiment conversion case
- 108. Convert an ordered array into a binary search tree
- Amazon cloud technology entry Resource Center, easy access to the cloud from 0 to 1
- Leetcode0587. 安装栅栏(difficult)
猜你喜欢

kettle实验

DVWA range practice

高薪程序员&面试题精讲系列91之Limit 20000加载很慢怎么解决?如何定位慢SQL?

Three challenges that a successful Devops leader should be aware of
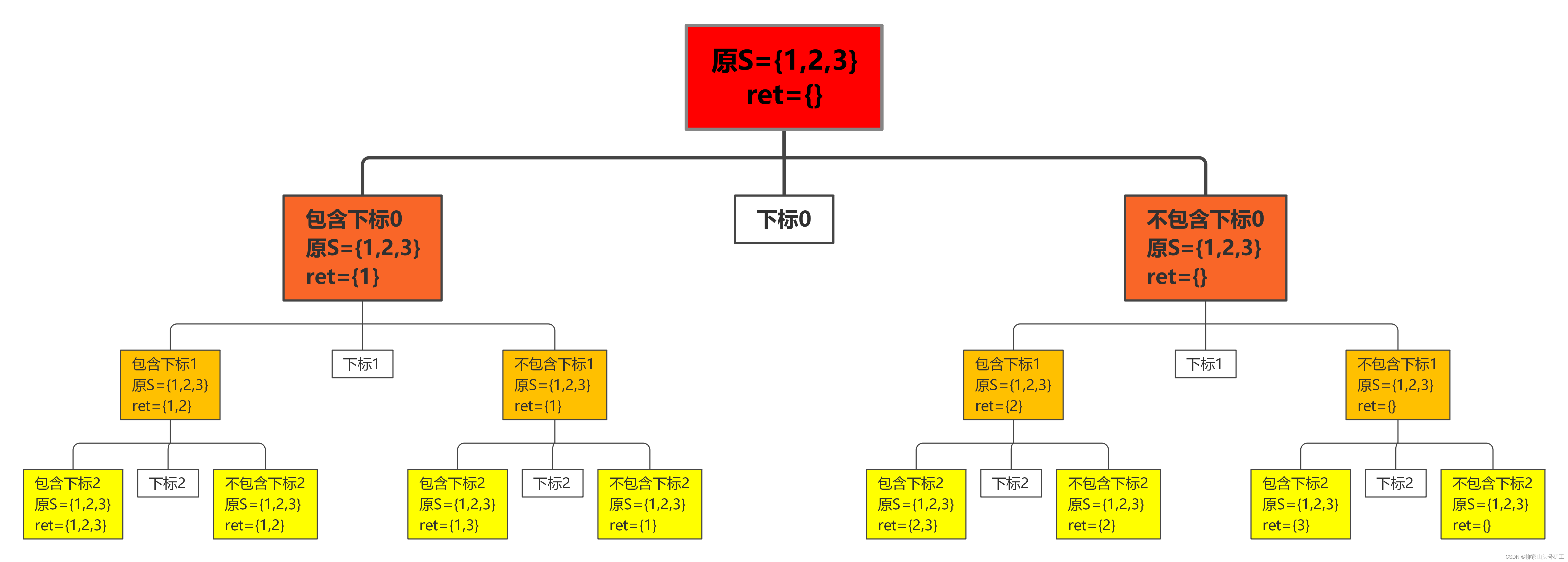
Leetcode question bank 78 Subset (recursive C implementation)

Dropout技术之随机神经元与随机深度

JS DOM event

Applet error: cannot read property'currenttarget'of undefined

Comparison of overloading, rewriting and hiding

Installation of data cleaning ETL tool kettle
随机推荐
如何实现根据照片获取地理位置及如何防御照片泄漏地理位置
Set the maximum width of the body, but why does the background color of the body cover the whole page?
Give the method of instantiating the object to the new object
SAP pi / PO function operation status monitoring and inspection
[educational codeforces round 80] problem solving Report
Solving Lucas number and combination theorem
AI上推荐 之 MMOE(多任务yyds)
What is monitoring intelligent playback and how to use intelligent playback to query video recording
Amazon cloud technology entry Resource Center, easy access to the cloud from 0 to 1
Simple understanding of arguments in JS
《数字电子技术基础》3.1 门电路概述、3.2 半导体二极管门电路
Kettle实验 (三)
KVM installation and deployment
JS DOM learn three ways to create elements
kernel-pwn学习(4)--Double Fetch&&0CTF2018-baby
ES-aggregation聚合分析
Summary of common concepts and problems of linear algebra in postgraduate entrance examination
Redis 过期 key 清理删除策略汇总
Chapter VIII project stakeholder management of information system project manager summary
Using sqlmap injection to obtain the account and password of the website administrator