What is a vector ？

From the perspective of Physics

From the perspective of Physics , A vector is an arrow in space , Determine the characteristics of the vector as its length and its direction , As long as the two characteristics are the same , You can move a vector freely and keep it unchanged .

A vector in a plane is two-dimensional , And the vector in the space we live in is three-dimensional .

From the perspective of computer science

From the perspective of Computer Science , A vector is an ordered list of numbers .

for example , Suppose we analyze house prices , You can use two-dimensional vectors to model houses . The first number represents the area of the house , The second number indicates the price .

ad locum ,“ vector ” nothing but “ list ” A fancy expression of .

The reason why this vector is two-dimensional , Because the length of this list is 2.

From the perspective of Mathematics

From the perspective of Mathematics , Vectors can make anything , Just need it to make sense .

The coordinates of a two-dimensional vector

The coordinates of a vector consist of a logarithm , This logarithm guides you from the origin （ Vector starting point ） Set out to reach its tip （ Vector end point ）.

The first number tells you to follow $x$ How far does the axis go , The second number tells you to follow $y$ How far does the axis go .

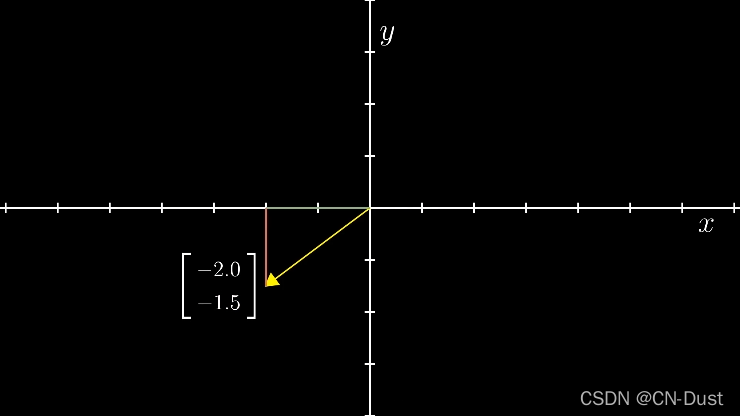
For example, the following vector , Just along $x$ Axis travel $-2.0$ Unit length , Then along $y$ Axis travel $-1.5$ Unit length . When the length is negative , That is to walk in the opposite direction to the positive direction .

The coordinates of a three-dimensional vector

Based on the two-dimensional coordinate system , Add perpendicular to $x$ Axis and $y$ The third axis of the shaft , Call it $z$ Axis .

under these circumstances , Each vector has an ordered array of three primitives corresponding to it . The first number tells you to follow $x$ How far does the axis go , The second number tells you to follow $y$ How far does the axis go , The third number tells you to follow $z$ How far does the axis go .

Vector addition and vector number multiplication

Vector addition

Suppose two vectors in the graph are added , Let's comment on the second vector , Make its starting point coincide with the end of the first vector .

Then draw a vector , It starts from the starting point of the first vector , Point to the end of the second vector .

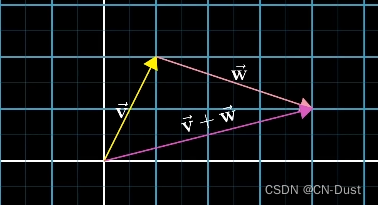
This vector is their sum .
From a numerical point of view , The coordinates of the first vector are $\left[\begin{array}{l}1\\ 2\end{array}\right]$, The coordinates of the second vector are $\left[\begin{array}{l}3\\ -1\end{array}\right]$.

It's not hard to find out , The sum vector is equal to moving to the right first $(1+3)$ Step , Move up again $(2-1)$ Step .

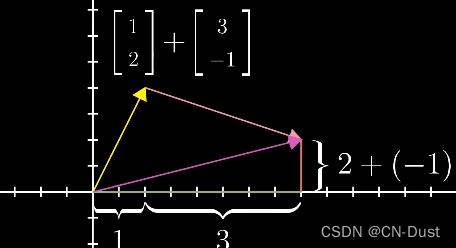
So the sum vector is ：
$$\left[\begin{array}{l}1\\ 2\end{array}\right]+\left[\begin{array}{l}3\\ -1\end{array}\right]=\left[\begin{array}{l}1+3\\ 2+(-1)\end{array}\right]$$

The addition of vectors is to add up the corresponding numbers .
$$\left[\begin{array}{l}{x}_1\\ y_1\end{array}\right]+\left[\begin{array}{l}{x}_2\\ y_2\end{array}\right]=\left[\begin{array}{l}{x}_1+x_2\\ y_1+y_2\end{array}\right]$$

Vector number times

Vector number multiplication is to lengthen the vector to the original n times .
for example ：


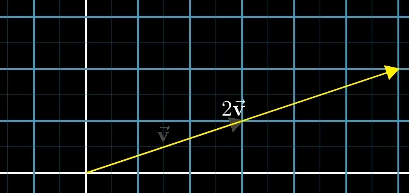
there $n$ Not having the property of a vector , It's called Scalar .

Coordinate system

In general ,$x$ The positive length of the shaft is 1 The vector of and $y$ The positive length of the shaft is 1 The vector of forms a coordinate system , however , We can also customize these two unit vectors , To change our coordinate system .

Zhang Cheng's space

$\vec{v}$ And $\vec{w}$ The vector set of all linear combinations is called “ Zhang Cheng's space ”.

When $\vec{v}$ And $\vec{w}$ When it's not collinear , The space formed is a plane .

When $\vec{v}$ And $\vec{w}$ Collinear , The space formed is a straight line .

When $\vec{v}$ And $\vec{w}$ All for $\vec{0}$ when , The origin of the space is .

Of course , This also applies to three-dimensional coordinate systems .

$\vec{v}$ And $\vec{w}$ And $\vec{u}$ The vector set of all linear combinations is called “ Zhang Cheng's space ”.