二分搜索的三个常见应用场景

寻找一个数（基本的二分搜索）

• 这个场景是最简单的，可能也是大家最熟悉的，即搜索一个数，如果存在，返回其索引，否则返回 -1。

int binarySearch(int[] nums, int target) {
    int left = 0; 
    int right = nums.length - 1; // 注意

    while(left <= right) {
        int mid = left + (right - left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; // 注意
        else if (nums[mid] > target)
            right = mid - 1; // 注意
    }
    return -1;
}

• 因为索引大小为 nums.length 是越界的。我们这算法中使用的是 [left, right] 两端都闭的区间。这个区间其实就是每次进行搜索的区间。

• while(left <= right) 的终止条件是 left == right + 1，写成区间的形式就是 [right + 1, right]，或者带个具体的数字进去 [3, 2]，可见这时候区间为空，因为没有数字既大于等于 3 又小于等于 2 的吧。所以这时候 while 循环终止是正确的，直接返回 -1 即可。
• while(left < right) 的终止条件是 left == right，写成区间的形式就是 [right, right]，或者带个具体的数字进去 [2, 2]，这时候区间非空，还有一个数 2，但此时 while 循环终止了。也就是说这区间 [2, 2] 被漏掉了，索引 2 没有被搜索，如果这时候直接返回 -1 就是错误的。
• 所以当都是左闭右闭的时候，我们判断的条件是left<=right
• 缺陷：比如说给你有序数组 nums = [1,2,2,2,3]，target 为 2，此算法返回的索引是 2，没错。但是如果我想得到 target 的左侧边界，即索引 1，或者我想得到 target 的右侧边界，即索引 3，这样的话此算法是无法处理

寻找左侧边界的二分搜索

 private int left_bound(int[] nums, int target) {
        //找到这个数的最右边的边界
        int left=0;
        int right=nums.length-1;
        while (left<=right){
            int mid=left+(right-left)/2;
            if (nums[mid]<target){
                left=mid+1;
            }else if(nums[mid]>target){
                right=mid-1;
            }else {
                right=mid-1;
            }
        }
        //走到这里,说明left肯定大于right了
        //一种情况,当这个值比数组的所有值都大,肯定会走到头left=length
        //比如 1 2 2 2 3 找2
        // left right mid
        //  0     4    2
        //  0     1    0
        //  1     1    1
        //  1     0
        // 1 2 3 5 7 8
        //  0     5     2
        //  0     1     0
        //  1     1     1
        //  1     0
        if (left>=nums.length||nums[left]!=target){
            return -1;
        }
        return left;
    }

• 这里使用还是左闭右闭的区间[left,right]

为什么该算法能够搜索左侧边界？

答：关键在于对于 nums[mid] == target 这种情况的处理：

if (nums[mid] == target) {
            // 别返回，锁定左侧边界
            right = mid - 1;
        }

• 可见，找到 target 时不要立即返回，而是缩小「搜索区间」的上界 right，在区间 [left, mid-1]中继续搜索，即不断向左收缩，达到锁定左侧边界的目的。

寻找右侧边界的二分查找 

 private int right_bound(int[] nums, int target) {
        int left=0;
        int right=nums.length-1;
        while (left<=right){
            int mid=left+(right-left);
            if (nums[mid]>target){
                right=mid-1;
            }else if (nums[mid]<target){
                left=mid+1;
            }else {
                left=mid+1;
            }
        }
        // 1 2 2 2 3
        // left  right mid
        // 0      4     2
        // 3      4     3
        // 4      4     4
        // 4      3
        // 1 2 3 5 7 8
        //  0     5     2
        //  0     1     0
        //  1     1     1
        //  2     1
        if (right<0||nums[right]!=target){
            return -1;
        }
        return right;
    }

• 、这里的区间还是[left,right)

为什么这个算法能够找到右侧边界？

if (nums[mid] == target) {
            // 别返回，锁定右侧边界
            left = mid + 1;
        }

• 当 nums[mid] == target 时，不要立即返回，而是增大「搜索区间」的左边界 left，使得区间不断向右靠拢，达到锁定右侧边界的目的。

为什么最后返回 left - 1 而不像左侧边界的函数，返回 left？而且我觉得这里既然是搜索右侧边界，应该返回 right 才对。

答：首先，while 循环的终止条件是 left == right，所以 left 和 right 是一样的，你非要体现右侧的特点，返回 right - 1 好了。

至于为什么要减一，这是搜索右侧边界的一个特殊点，关键在锁定右边界时的这个条件断：

// 增大 left，锁定右侧边界
if (nums[mid] == target) {
    left = mid + 1;
    // 这样想: mid = left - 1

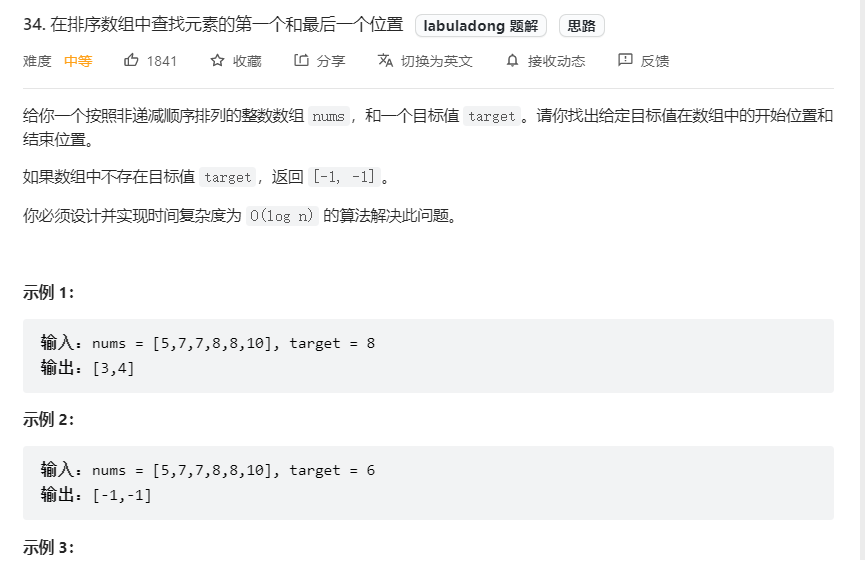
34. 在排序数组中查找元素的第一个和最后一个位置

 

 

class Solution {
     public int[] searchRange(int[] nums, int target) {
        return new int[]{left_bound(nums,target),right_bound(nums,target)};
    }

    private int left_bound(int[] nums, int target) {
        //找到这个数的最右边的边界
        int left=0;
        int right=nums.length-1;
        while (left<=right){
            int mid=left+(right-left)/2;
            if (nums[mid]<target){
                left=mid+1;
            }else if(nums[mid]>target){
                right=mid-1;
            }else {
                right=mid-1;
            }
        }
        //走到这里,说明left肯定大于right了
        //一种情况,当这个值比数组的所有值都大,肯定会走到头left=length
        //比如 1 2 2 2 3 找2
        // left mid right
        // 0     2     4
        // 0     0      1
        // 1     1      1
        // 1     0      0
        // 1 2 3 5 7 8
        // 0     2      5
        // 0     0       1
        // 1     1       1
        // 1     0       0
        if (left>=nums.length||nums[left]!=target){
            return -1;
        }
        return left;
    }

    private int right_bound(int[] nums, int target) {
        int left=0;
        int right=nums.length-1;
        while (left<=right){
            int mid=left+(right-left);
            if (nums[mid]>target){
                right=mid-1;
            }else if (nums[mid]<target){
                left=mid+1;
            }else {
                left=mid+1;
            }
        }
        // 1 2 2 2 3
        // left mid right
        // 0      2      4
        // 3      3      4
        // 4      4      4
        // 4      3      3
        if (right<0||nums[right]!=target){
            return -1;
        }
        return right;
    }
}

Offer 53

 

class Solution {
    public int search(int[] nums, int target) {
        int left=left_bound(nums,target);
        int right=right_bound(nums,target);
        if (left==-1){
            return 0;
        }
        return right-left+1;
    }



    private int left_bound(int[] nums, int target) {
        int left=0;
        int right=nums.length-1;

        while (left<=right){
            int mid=left+(right-left);
            if (nums[mid]<target){
                left=mid+1;
            }else if (nums[mid]>target){
                right=mid-1;
            }else {
                right=mid-1;
            }
        }
        if (left==nums.length||nums[left]!=target){
            return -1;
        }
        return left;
    }

    private int right_bound(int[] nums, int target) {
        int left=0;
        int right=nums.length-1;
        while (left<=right){
            int mid=left+(right-left);
            if (nums[mid]>target){
                right=mid-1;
            }else if (nums[mid]<target){
                left=mid+1;
            }else {
                left=mid+1;
            }
        }
        if (right<0||nums[right]!=target){
            return -1;
        }
        return right;
    }
}

 

Offer04 

 

• 从右上角开始找，如果大于就往一行的左边找，如果小于就往一列的下面找

 

class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
            if (matrix==null||matrix.length==0){
                return false;
            }
            return helper(matrix,target,0,matrix[0].length-1);
    }

    private boolean helper(int[][] matrix, int target, int row, int column) {
        if (row<0||row>=matrix.length||column<0||column>=matrix[0].length){
             return false;
        }else if (matrix[row][column]==target){
            return true;
        }else if (matrix[row][column]>target){
            return helper(matrix,target,row,column-1);
        }else {
            return helper(matrix,target,row+1,column);
        }
    }
}

Offer 11旋转数组的最小数字

 

class Solution {
         public int minArray(int[] numbers) {
        int n=numbers.length-1;
        int left=0;
        int right=n;
        while (left<right){
            int mid=left+(right-left)/2;
            if (numbers[mid]>numbers[right]){
                //说明mid在左区间
                left=mid+1;
            }else if(numbers[mid]<numbers[right]){
                //说明mid现在在右区间
                right=mid;
            }else {
                //当值相同的时候,我们不能判读在那个区间,因为
                //1 1 2 3 4 ->1 2 3 4 1
                //1 1 2 3 4 ->2 3 4 1 1
                right=right-1;
                //当确定不了的时候 我们就减少右边的范围,因为左边还存在相同的这个值
            }
        }
        return numbers[left];
    }
}

 

Offer 53 II

 

class Solution {
      public int missingNumber(int[] nums) {
        int left=0;
        int right=nums.length-1;
        while (left<=right){
            int mid=left+(right-left)/2;
            if (nums[mid]==mid){
                //说明mid之前都没问题
                left=mid+1;
            }else if (nums[mid]!=mid){
                //说明mid之前有问题
                right=mid-1;
            }
        }
        return left;
    }

}