当前位置:网站首页>Intuitive understanding entropy
Intuitive understanding entropy
2022-04-23 10:48:00 【qq1033930618】
List of articles
One 、 Information entropy
H ( X ) = − ∑ i = 1 n p ( x i ) l o g p ( x i ) H\left(X\right)=-\sum_{i=1}^{n}p\left(x_i\right)logp\left(x_i\right) H(X)=−∑i=1np(xi)logp(xi)
The larger the information entropy, the more chaotic The higher the uncertainty The closer to uniform distribution Less information
n Random variables may take values
x A random variable
p(x) A random variable x The probability function of
No matter who the base of the logarithm is, it has no effect General with 10 Base number
Two 、 Relative entropy KL The divergence
D K L ( p ∣ ∣ q ) = ∑ i = 1 n p ( x i ) l o g p ( x i ) q ( x i ) D_{KL}\left(p||q\right)=\sum_{i=1}^{n}{p\left(x_i\right)log\frac{p\left(x_i\right)}{q\left(x_i\right)}} DKL(p∣∣q)=∑i=1np(xi)logq(xi)p(xi)
An asymmetric measure of the difference between two probability distributions
The distance between two different distributions of the same random variable
Asymmetry only PQ The probability distribution is exactly the same
Nonnegativity only PQ If the probability distribution is exactly the same, it will be equal to 0
You can write cross entropy minus information entropy
D K L ( p ∣ ∣ q ) = ∑ i = 1 n p ( x i ) l o g p ( x i ) q ( x i ) D_{KL}\left(p||q\right)=\sum_{i=1}^{n}{p\left(x_i\right)log\frac{p\left(x_i\right)}{q\left(x_i\right)}} DKL(p∣∣q)=∑i=1np(xi)logq(xi)p(xi)
= ∑ i = 1 n p ( x i ) l o g p ( x i ) − ∑ i = 1 n p ( x i ) l o g q ( x i ) =\sum_{i=1}^{n}p\left(x_i\right)logp\left(x_i\right)-\sum_{i=1}^{n}p\left(x_i\right)logq\left(x_i\right) =∑i=1np(xi)logp(xi)−∑i=1np(xi)logq(xi)
= H ( P , Q ) − H ( P ) =H\left(P,Q\right)-H\left(P\right) =H(P,Q)−H(P)
3、 ... and 、 Cross entropy
Measure the predicted distribution of random variables Q And real distribution P disparity
The distribution distance of Yueming novel is small
Only related to the prediction probability of the real label
Because unreal labels P(x)=0 Multiply any number to be 0
H ( P , Q ) = − ∑ i = 1 n p ( x i ) l o g q ( x i ) H\left(P,Q\right)=-\sum_{i=1}^{n}p\left(x_i\right)logq\left(x_i\right) H(P,Q)=−∑i=1np(xi)logq(xi)
H ( P , Q ) = ∑ x p ( x ) l o g 1 q ( x ) H\left(P,Q\right)=\sum_{x}{p\left(x\right)log\frac{1}{q\left(x\right)}} H(P,Q)=∑xp(x)logq(x)1
Most simplified formula Only real label predictions are calculated
C r o s s E n t r o p y ( p , q ) = − l o g q ( c i ) CrossEntropy\left(p,q\right)=-logq\left(c_i\right) CrossEntropy(p,q)=−logq(ci)
II. Classification formula
H ( P , Q ) = ∑ x p ( x ) l o g 1 q ( x ) H\left(P,Q\right)=\sum_{x}{p\left(x\right)log\frac{1}{q\left(x\right)}} H(P,Q)=∑xp(x)logq(x)1
= ( p ( x 1 ) l o g q ( x 1 ) + p ( x 2 ) l o g q ( x 2 ) ) =\left(p\left(x_1\right)logq\left(x_1\right)+p\left(x_2\right)logq\left(x_2\right)\right) =(p(x1)logq(x1)+p(x2)logq(x2))
= ( p l o g q + ( 1 − p ) l o g ( 1 − q ) ) =\left(plogq+\left(1-p\right)log\left(1-q\right)\right) =(plogq+(1−p)log(1−q))
p ( x 1 ) = p p\left(x_1\right)=p p(x1)=p
p ( x 2 ) = 1 − p p\left(x_2\right)=1-p p(x2)=1−p
q ( x 1 ) = q q\left(x_1\right)=q q(x1)=q
q ( x 2 ) = 1 − q q\left(x_2\right)=1-q q(x2)=1−q
The information entropy of real distribution is 0
here KL Divergence is equal to cross entropy
If there is no real distribution, then KL The divergence
CrossEntropyLoss()
entropy = nn.CrossEntropyLoss()
input = torch.tensor([[-0.7715,-0.6205,-0.2562]])
target = torch.tensor([0])
output = entropy(input, target)
l o s s ( x , c l a s s ) = − l o g e x p ( x [ c l a s s ] ) ∑ j e x p ( x [ j ] ) = − x [ c l a s s ] + l o g ∑ j e x p ( x [ j ] ) loss\left(x,class\right)=-log\frac{exp\left(x\left[class\right]\right)}{\sum_{j}exp\left(x\left[j\right]\right)}=-x\left[class\right]+log\sum_{j}exp\left(x\left[j\right]\right) loss(x,class)=−log∑jexp(x[j])exp(x[class])=−x[class]+log∑jexp(x[j])
Pay attention to e Base number
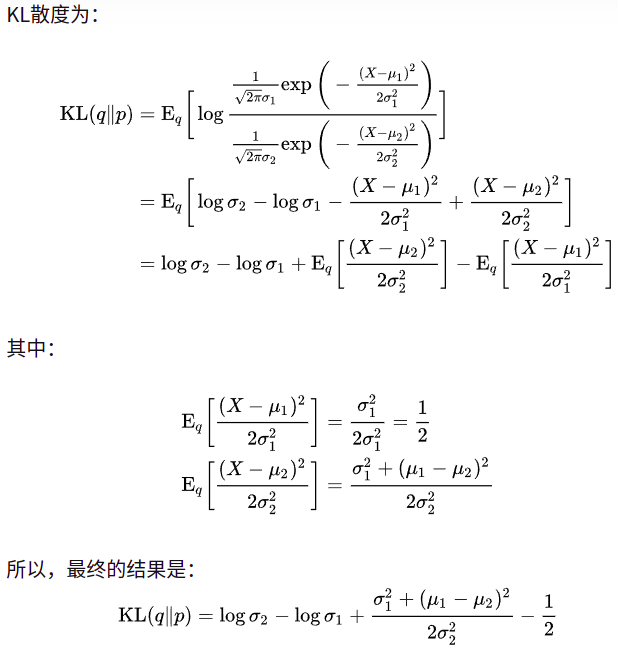
Four 、 Normal distribution KL The divergence
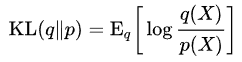

版权声明
本文为[qq1033930618]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204230618497006.html
边栏推荐
- App. In wechat applet JS files, components, APIs
- [Niuke challenge 47] C. conditions (BitSet acceleration Floyd)
- Arbitrary file reading vulnerability exploitation Guide
- 59、螺旋矩阵(数组)
- Image processing - Noise notes
- Define linked list (linked list)
- Cve-2019-0708 vulnerability exploitation of secondary vocational network security 2022 national competition
- Notes on concurrent programming of vegetables (V) thread safety and lock solution
- 中职网络安全2022国赛之CVE-2019-0708漏洞利用
- SQL Server cursor circular table data
猜你喜欢

MySQL how to merge the same data in the same table

Notes on concurrent programming of vegetables (IX) asynchronous IO to realize concurrent crawler acceleration

Charles function introduction and use tutorial

JUC concurrent programming 09 -- source code analysis of condition implementation

【leetcode】199. Right view of binary tree

Ueditor -- limitation of 4m size of image upload component

Solution architect's small bag - 5 types of architecture diagrams

Cve-2019-0708 vulnerability exploitation of secondary vocational network security 2022 national competition

Reading integrity monitoring techniques for vision navigation systems - 5 Results

Idea - indexing or scanning files to index every time you start
随机推荐
SQL Server recursive query of superior and subordinate
JVM——》常用命令
Sim Api User Guide(5)
Sim Api User Guide(7)
Solve the problem of installing VMware after uninstalling
Solution architect's small bag - 5 types of architecture diagrams
任意文件读取漏洞 利用指南
微信小程序中app.js文件、组件、api
Solution architect's small bag - 5 types of architecture diagrams
242、有效字母异位词(哈希表)
Installing MySQL with CentOS / Linux
How can swagger2 custom parameter annotations not be displayed
24. Exchange the nodes in the linked list (linked list)
Sim Api User Guide(4)
Idea - indexing or scanning files to index every time you start
142、环形链表||
707、设计链表(链表)
Hikvision face to face summary
部署jar包
202、快乐数