当前位置:网站首页>线段相交的应用
线段相交的应用
2022-08-09 20:11:00 【51CTO】
线段相交是计算几何的基础知识,有必要熟练掌握。
关于叉积:

如果叉积结果大于0,表示p2-p0在p0-p1的逆时针方向(图中例子结果为4);如果叉积结果小于0,表示p2-p0在p0-p1的顺时针方向;如果叉积结果是0,那么3点共线。【这很好理解:向量积|c|=|a×b|=|a| |b|sin<a,b>。】
判断线段相交:
bool Cross(point a,point b,point c,point d){//判断ab 与cd是否相交
double re1,re2,re3,re4;
re1=crossmulti(c,d,a);
re2=crossmulti(c,d,b);
re3=crossmulti(a,b,c);
re4=crossmulti(a,b,d);
if(re1*re2
<
0&&re3*re4
<0)return 1;
else if(re1==0
&
&OnSegment(c,d,a))return 1; //四种在同一条线上的结果
else if(re2==0
&
&OnSegment(c,d,b))return 1;
else if(re3==0
&
&OnSegment(a,b,c))return 1;
else if(re4==0
&
&OnSegment(a,b,d))return 1;
return 0;
}
“if(re1*re2
<
0&&re3*re4
<0)return 1; ”:
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.

“else if(re1==0&&OnSegment(c,d,a))return 1; ”:

剩余三种是三种类似。
则保证了第三个点在前两个点所构成的矩形之内:
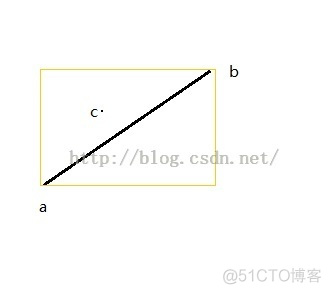
所以,在re1==0成立的基础上,OnSegment(c,d,a)排除了第三个点a在c,d的延长线的情况,一定在线上。
线段相交的简单应用:
hdu 1086 You can Solve a Geometry Problem too
题目: http://acm.hdu.edu.cn/showproblem.php?pid=1086 算是模板题吧。
#include <iostream>
#include <cstdio>
#include<algorithm>
using
namespace
std;
const
int
maxn
=
105;
struct
point{
double
x,
y;
};
struct
node{
point
a,
b;
}
edge[
maxn];
double
crossmulti(
point
a,
point
b,
point
c){
return (
b.
x
-
a.
x)
*(
c.
y
-
a.
y)
-(
b.
y
-
a.
y)
*(
c.
x
-
a.
x);
}
bool
OnSegment(
point
a,
point
b,
point
c){
if(
c.
x
>=
min(
a.
x,
b.
x)
&&
c.
x
<=
max(
a.
x,
b.
x)
&&
c.
y
>=
min(
a.
y,
b.
y)
&&
c.
y
<=
max(
a.
y,
b.
y))
return
1;
return
0;
}
bool
Cross(
point
a,
point
b,
point
c,
point
d){
double
re1,
re2,
re3,
re4;
re1
=
crossmulti(
c,
d,
a);
re2
=
crossmulti(
c,
d,
b);
re3
=
crossmulti(
a,
b,
c);
re4
=
crossmulti(
a,
b,
d);
if(
re1
*
re2
<
0
&&
re3
*
re4
<
0)
return
1;
else
if(
re1
==
0
&&
OnSegment(
c,
d,
a))
return
1;
else
if(
re2
==
0
&&
OnSegment(
c,
d,
b))
return
1;
else
if(
re3
==
0
&&
OnSegment(
a,
b,
c))
return
1;
else
if(
re4
==
0
&&
OnSegment(
a,
b,
d))
return
1;
return
0;
}
int
main()
{
//freopen("cin.txt","r",stdin);
int
n;
point
p1,
p2;
while(
cin
>>
n
&&
n){
int
ans
=
0;
for(
int
i
=
0;
i
<
n;
i
++){
scanf(
"%lf%lf%lf%lf",
&
p1.
x,
&
p1.
y,
&
p2.
x,
&
p2.
y);
edge[
i].
a
=
p1;
edge[
i].
b
=
p2;
for(
int
j
=
0;
j
<
i;
j
++){
//单向
if(
Cross(
edge[
i].
a,
edge[
i].
b,
edge[
j].
a,
edge[
j].
b))
ans
++;
}
}
printf(
"%d\n",
ans);
}
return
0;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
fzu 1015 土地划分
题目:
http://acm.fzu.edu.cn/problem.php?pid=1015
当前线段的终点就是下一个线段的起点。问,能把矩形划成几份?
分析:画一条边构成的土地数量就是f(1)=2,两条线段就是 f(2)=4,通过画图可以发现,每增加一条边,部分其他边会分割它,由此增加L+1条线段(L表示分割它的边数,也就是交点数),一条线段将空间分成两 份,增加一份,所以f(n)=f(n-1)+Ln+1=f(n-2)+L(n- 1)+1+Ln+1=……=f(1)+L2+1+……+Ln+1=2+L2+L3+……+Ln+n-1=n+1+∑Li. 结果与边数和总的交点数相关。注意本题中端点接触不算严格相交。
#include <iostream>
#include <cstdio>
using
namespace
std;
const
int
maxn
=
60;
struct
point{
int
x,
y;
};
struct
vect{
point
s,
e;
}
v[
maxn];
int
multi(
point
p1,
point
p2,
point
p0){
return (
p1.
x
-
p0.
x)
*(
p2.
y
-
p0.
y)
-(
p2.
x
-
p0.
x)
*(
p1.
y
-
p0.
y);
}
bool
OnSegment(
point
p1,
point
p2,
point
p0){
if(
p0.
x
<=
max(
p1.
x,
p2.
x)
&&
p0.
x
>=
min(
p1.
x,
p2.
x)
&&
p0.
y
<=
max
(
p1.
y,
p2.
y)
&&
p0.
y
>=
min(
p1.
y,
p2.
y))
return
1;
return
0;
}
bool
cross(
vect
l1,
vect
l2){
int
r1,
r2,
r3,
r4;
r1
=
multi(
l2.
s,
l2.
e,
l1.
s);
r2
=
multi(
l2.
s,
l2.
e,
l1.
e);
r3
=
multi(
l1.
s,
l1.
e,
l2.
s);
r4
=
multi(
l1.
s,
l1.
e,
l2.
e);
if(
r1
*
r2
<
0
&&
r3
*
r4
<
0)
return
1;
//else if(r1==0&&OnSegment(l2.s,l2.e,l1.s)) return 1;
//else if(r2==0&&OnSegment(l2.s,l2.e,l1.e)) return 1;
//else if(r3==0&&OnSegment(l1.s,l1.e,l2.s)) return 1;
//else if(r4==0&&OnSegment(l1.s,l1.e,l2.e)) return 1;
else
return
0;
}
int
main()
{
//freopen("cin.txt","r",stdin);
int
w,
h,
l;
while(
~scanf(
"%d%d",
&
w,
&
h)
&&(
w
+
h)){
scanf(
"%d",
&
l);
point
p1,
p2;
int
cnt
=
0;
scanf(
"%d%d",
&
p1.
x,
&
p1.
y);
for(
int
i
=
0;
i
<
l;
i
++){
scanf(
"%d%d",
&
p2.
x,
&
p2.
y);
v[
cnt].
s
=
p1;
v[
cnt
++].
e
=
p2;
p1
=
p2;
}
int
L
=
0;
for(
int
i
=
0;
i
<
cnt;
i
++){
for(
int
j
=
i
+
1;
j
<
cnt;
j
++){
if(
cross(
v[
i],
v[
j])){
L
++;
}
}
}
printf(
"%d\n",
L
+
l
+
1);
}
return
0;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
还有一些问题,不但要求判断是否线段相交,还需要求出其交点坐标。

图中P是AB和DC的交点。
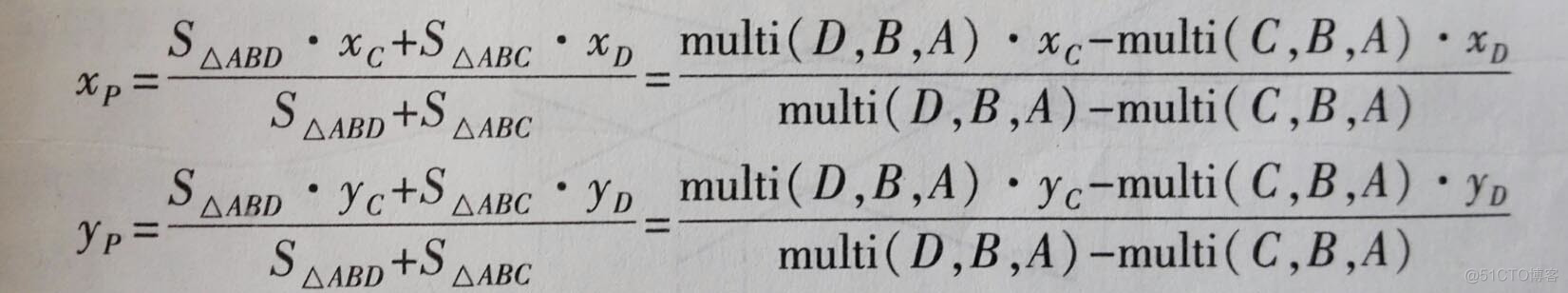
poj 1269 Intersecting Lines(线段的二维关系·交点坐标)
题目:
http://poj.org/problem?id=1269
大意:判断线段的平面关系,平行,相交,重叠。注意,有一种未接触相交的空间关系,所以不能直接套用跨立排斥算法。
#include <iostream>
#include <cstdio>
using
namespace
std;
struct
point{
int
x,
y;
}
p[
4];
struct
node{
double
x,
y;
}
po;
int
multi(
point
p1,
point
p2,
point
p0){
return (
p1.
x
-
p0.
x)
*(
p2.
y
-
p0.
y)
-(
p2.
x
-
p0.
x)
*(
p1.
y
-
p0.
y);
}
int
judge(){
int
r1,
r2,
r3,
r4;
r1
=
multi(
p[
0],
p[
2],
p[
3]);
r2
=
multi(
p[
1],
p[
2],
p[
3]);
if(
r1
==
0
&&
r2
==
0)
return
1;
//重合
if((
p[
0].
x
-
p[
1].
x)
*(
p[
2].
y
-
p[
3].
y)
==(
p[
0].
y
-
p[
1].
y)
*(
p[
2].
x
-
p[
3].
x))
return
3;
//平行
return
2;
//相交
}
int
main()
{
//freopen("cin.txt","r",stdin);
int
n;
cin
>>
n;
printf(
"INTERSECTING LINES OUTPUT\n");
while(
n
--){
for(
int
i
=
0;
i
<
4;
i
++)
scanf(
"%d%d",
&
p[
i].
x,
&
p[
i].
y);
int
res
=
judge();
if(
res
==
1)
puts(
"LINE");
else
if(
res
==
3)
puts(
"NONE");
else {
int
q1,
q2;
q1
=
multi(
p[
3],
p[
0],
p[
1])
*
p[
2].
x
-
multi(
p[
2],
p[
0],
p[
1])
*
p[
3].
x;
q2
=
multi(
p[
3],
p[
0],
p[
1])
-
multi(
p[
2],
p[
0],
p[
1]);
po.
x
=
q1
*
1.0
/
q2;
q1
=
multi(
p[
3],
p[
0],
p[
1])
*
p[
2].
y
-
multi(
p[
2],
p[
0],
p[
1])
*
p[
3].
y;
po.
y
=
q1
*
1.0
/
q2;
printf(
"POINT %.2lf %.2lf\n",
po.
x,
po.
y);
}
}
printf(
"END OF OUTPUT\n");
return
0;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
边栏推荐
猜你喜欢
随机推荐
一种基于连接和安全熵的网络空间整体安全认识和方法
Unity_平滑移动
分数阶混沌系统李雅普指数和分岔图
访问控制知识
buuctf (Adventure 2)
tki-tree 树组件控制默认展开第几层数据
如何在WPF中设置Grid ColumnDefinitions的样式
下秒数据:湖仓一体带来的现代数据堆栈变革开始了
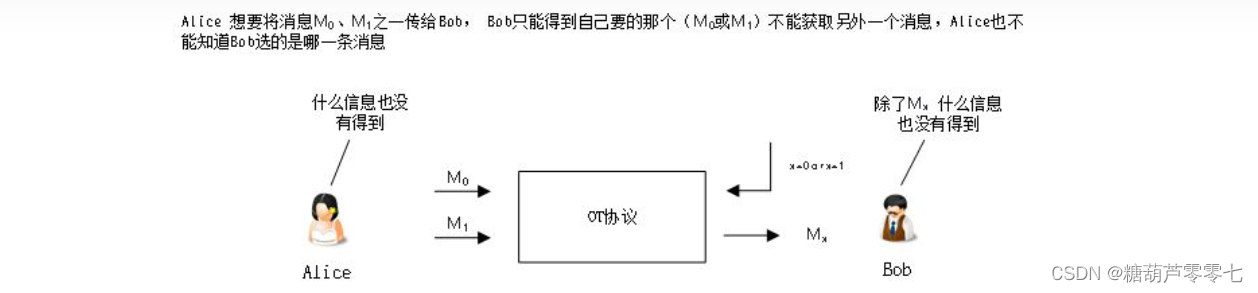
不经意传输协议OT
MySQL Notes-06 Basic SQL Operations
DSPE-PEG-PDP,DSPE-PEG-OPSS,磷脂-聚乙二醇-巯基吡啶可减少肽的免疫原性
FS4066耐高压1到4节内置MOS的锂电池充电管理芯片
Interviewer: How to deal with Redis big key?
Problems with compiling SIP with QGIS
matlab 神经网络 ANN 分类
Win11搜索不到文件的解决方法
Daily practice of PMP | Do not get lost in the exam -8.8 (including agility + multiple choice)
凸集与凸函数
prometheus学习3Grafana部署及基本使用
[corctf 2022] section





![[corctf 2022] 部分](/img/03/ee1ead55805a2ac690ec79c675c3e6.png)