当前位置:网站首页>P1390 公约数的和(莫比乌斯反演)
P1390 公约数的和(莫比乌斯反演)
2022-04-23 06:21:00 【Zimba_】
题意:
给定 n n n,求 ∑ i = 1 n ∑ j = i + 1 n g c d ( i , j ) \sum_{i=1}^{n}\sum_{j=i+1}^{n}gcd(i,j) ∑i=1n∑j=i+1ngcd(i,j)。 ( n < = 2 e 6 ) (n<=2e6) (n<=2e6)
推导:
第一步,按套路先把 g c d gcd gcd提到前面来,
∑ g = 1 n g ∑ i = 1 n ∑ j = i + 1 n [ g = g c d ( i , j ) ] \sum_{g=1}^{n}g\sum_{i=1}^{n}\sum_{j=i+1}^{n}[g=gcd(i,j)] ∑g=1ng∑i=1n∑j=i+1n[g=gcd(i,j)]
第二步,我们令 f ( g ) = ∑ i = 1 n ∑ j = i + 1 n [ g = g c d ( i , j ) ] f(g)=\sum_{i=1}^{n}\sum_{j=i+1}^{n}[g=gcd(i,j)] f(g)=∑i=1n∑j=i+1n[g=gcd(i,j)],此时我们要求的东西就是 ∑ g = 1 n g f ( g ) \sum_{g=1}^{n}gf(g) ∑g=1ngf(g),先放着。
然后这时候我们在莫比乌斯反演的公式中二选一,有经验之后就知道该选哪个了。
我们令,
F ( g ) = ∑ g ∣ d f ( d ) F(g)=\sum_{g|d}f(d) F(g)=∑g∣df(d)
= ∑ g ∣ d ∑ i = 1 n ∑ j = i + 1 n [ d = g c d ( i , j ) ] \;\;\;\;\;\;\;\;=\sum_{g|d}\sum_{i=1}^{n}\sum_{j=i+1}^{n}[d=gcd(i,j)] =∑g∣d∑i=1n∑j=i+1n[d=gcd(i,j)]
= ∑ i = 1 n ∑ j = i + 1 n [ g ∣ g c d ( i , j ) ] \;\;\;\;\;\;\;\;=\sum_{i=1}^{n}\sum_{j=i+1}^{n}[g|gcd(i,j)] =∑i=1n∑j=i+1n[g∣gcd(i,j)]
= ∑ i = 1 n ∑ j = i + 1 n [ g ∣ i ∧ g ∣ j ] \;\;\;\;\;\;\;\;=\sum_{i=1}^{n}\sum_{j=i+1}^{n}[g|i\wedge g|j] =∑i=1n∑j=i+1n[g∣i∧g∣j]
= 1 2 ( ⌊ n g ⌋ ⌊ n g ⌋ − ⌊ n g ⌋ ) \;\;\;\;\;\;\;\;=\frac{1}{2} (\lfloor \frac{n}{g} \rfloor \lfloor \frac{n}{g} \rfloor -\lfloor \frac{n}{g} \rfloor) =21(⌊gn⌋⌊gn⌋−⌊gn⌋)
根据反演公式,有 f ( g ) = ∑ g ∣ d μ ( d g ) F ( d ) f(g)=\sum_{g|d}\mu(\frac{d}{g})F(d) f(g)=∑g∣dμ(gd)F(d)
所以我们最后代回原来要求的式子中,
∑ g = 1 n g f ( g ) = ∑ g n ∑ g ∣ d μ ( d g ) F ( d ) \sum_{g=1}^{n}gf(g)=\sum_{g}^{n}\sum_{g|d}\mu(\frac{d}{g})F(d) ∑g=1ngf(g)=∑gn∑g∣dμ(gd)F(d)
前面推过了, F ( d ) F(d) F(d)可以 o ( 1 ) o(1) o(1)算,莫比乌斯函数可以预处理,所以最后的式子就可以 o ( n l o g n ) o(nlogn) o(nlogn)求出来了。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
typedef pair<int,int> P;
const ll MAXN=2000000;
ll prime[MAXN+10],notPrime[MAXN+10],mu[MAXN+10],tot;
void initMu(ll n)
{
notPrime[1]=mu[1]=1;
for(ll i=2;i<=n;i++)
{
if(!notPrime[i])prime[tot++]=i,mu[i]=-1;
for(ll j=0;j<tot&&i*prime[j]<=n;j++)
{
notPrime[i*prime[j]]=1;
if(i%prime[j])mu[i*prime[j]]=-mu[i];
else {
mu[i*prime[j]]=0;break;}
}
}
}
ll n;
ll getF(ll g)
{
ll t=n/g;
return (t*t-t)/2;
}
int main()
{
initMu(MAXN);
scanf("%lld",&n);
ll ans=0;
for(ll g=1;g<=n;g++)
{
for(ll d=g;d<=n;d+=g)
{
ans=ans+g*mu[d/g]*getF(d);
}
}
printf("%lld\n",ans);
return 0;
}
版权声明
本文为[Zimba_]所创,转载请带上原文链接,感谢
https://blog.csdn.net/weixin_43785386/article/details/107814580
边栏推荐
- 后台管理系统框架,总有你想要的
- 商业版阿里MQ普通消息发送订阅Demo
- Beifeng communication helps Zhanjiang fire brigade build PDT wireless communication system
- golang实现一个带Web界面的五险一金计算器
- PyTorch 19. Differences and relations of similar operations in pytorch
- Draw margin curve in arcface
- 电力行业巡检对讲通信系统
- 记录阿里云服务器挖矿程序处理
- Typora语法详解(一)
- 如何将进程绑定到指定的CPU上
猜你喜欢

el-select 中v-model绑定值,数据回显只显示value,不显示label
Meishe technology launches professional video editing solution for desktop -- Meiying PC version

Typora操作技巧说明(一).md
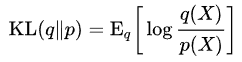
直观理解熵

广西电网|应急空天一体化通信系统方案

Machine vision series (02) -- tensorflow2 3 + win10 + GPU installation

Solution of self Networking Wireless Communication intercom system in Beifeng oil and gas field

Intuitive understanding of torch nn. Unfold

重大安保事件应急通信系统解决方案

可视化之路(九)Arrow类详解
随机推荐
Int8 quantification and inference of onnx model using TRT
使用el-popconfirm和el-backtop不生效
后台管理系统框架,总有你想要的
连接orcale
H5案例开发
[8] Assertion failed: dims. nbDims == 4 || dims. nbDims == 5
华为云MVP邮件
可视化常见问题解决方案(九)背景颜色问题
Flexible blind patch of ad hoc network | Beifeng oil and gas field survey solution
关于短视频技术轮廓探讨
北峰油气田自组网无线通信对讲系统解决方案
可视化常见绘图(四)柱状图
公专融合对讲机是如何实现多模式通信下的协同工作?
HQL语句的调优
各类日期转化的utils
Typora语法详解(一)
“泉”力以赴·同“州”共济|北峰人一直在行动
VScode
Source Insight 4.0常见问题
VIM使用