当前位置:网站首页>直观理解熵
直观理解熵
2022-04-23 06:19:00 【qq1033930618】
文章目录
一、信息熵
H ( X ) = − ∑ i = 1 n p ( x i ) l o g p ( x i ) H\left(X\right)=-\sum_{i=1}^{n}p\left(x_i\right)logp\left(x_i\right) H(X)=−∑i=1np(xi)logp(xi)
信息熵越大越混乱 不确定性越高 越接近均匀分布 信息越少
n 随机变量可能取值
x 随机变量
p(x) 随机变量x的概率函数
无论对数以谁为底数都没有影响 一般以10为底数
二、相对熵KL散度
D K L ( p ∣ ∣ q ) = ∑ i = 1 n p ( x i ) l o g p ( x i ) q ( x i ) D_{KL}\left(p||q\right)=\sum_{i=1}^{n}{p\left(x_i\right)log\frac{p\left(x_i\right)}{q\left(x_i\right)}} DKL(p∣∣q)=∑i=1np(xi)logq(xi)p(xi)
两个概率分布差异非对称度量
同一个随机变量两个不同分布之间距离
非对称性 仅PQ概率分布完全一样才相等
非负性 仅PQ概率分布完全一样才相等为0
可以写作交叉熵减去信息熵
D K L ( p ∣ ∣ q ) = ∑ i = 1 n p ( x i ) l o g p ( x i ) q ( x i ) D_{KL}\left(p||q\right)=\sum_{i=1}^{n}{p\left(x_i\right)log\frac{p\left(x_i\right)}{q\left(x_i\right)}} DKL(p∣∣q)=∑i=1np(xi)logq(xi)p(xi)
= ∑ i = 1 n p ( x i ) l o g p ( x i ) − ∑ i = 1 n p ( x i ) l o g q ( x i ) =\sum_{i=1}^{n}p\left(x_i\right)logp\left(x_i\right)-\sum_{i=1}^{n}p\left(x_i\right)logq\left(x_i\right) =∑i=1np(xi)logp(xi)−∑i=1np(xi)logq(xi)
= H ( P , Q ) − H ( P ) =H\left(P,Q\right)-H\left(P\right) =H(P,Q)−H(P)
三、交叉熵
度量随机变量预测分布Q和真实分布P差距
越小说明分布距离小
只和真实标签的预测概率有关
因为非真实标签P(x)=0乘任何数都为0
H ( P , Q ) = − ∑ i = 1 n p ( x i ) l o g q ( x i ) H\left(P,Q\right)=-\sum_{i=1}^{n}p\left(x_i\right)logq\left(x_i\right) H(P,Q)=−∑i=1np(xi)logq(xi)
H ( P , Q ) = ∑ x p ( x ) l o g 1 q ( x ) H\left(P,Q\right)=\sum_{x}{p\left(x\right)log\frac{1}{q\left(x\right)}} H(P,Q)=∑xp(x)logq(x)1
最简化公式 仅计算真实标签预测
C r o s s E n t r o p y ( p , q ) = − l o g q ( c i ) CrossEntropy\left(p,q\right)=-logq\left(c_i\right) CrossEntropy(p,q)=−logq(ci)
二分类公式
H ( P , Q ) = ∑ x p ( x ) l o g 1 q ( x ) H\left(P,Q\right)=\sum_{x}{p\left(x\right)log\frac{1}{q\left(x\right)}} H(P,Q)=∑xp(x)logq(x)1
= ( p ( x 1 ) l o g q ( x 1 ) + p ( x 2 ) l o g q ( x 2 ) ) =\left(p\left(x_1\right)logq\left(x_1\right)+p\left(x_2\right)logq\left(x_2\right)\right) =(p(x1)logq(x1)+p(x2)logq(x2))
= ( p l o g q + ( 1 − p ) l o g ( 1 − q ) ) =\left(plogq+\left(1-p\right)log\left(1-q\right)\right) =(plogq+(1−p)log(1−q))
p ( x 1 ) = p p\left(x_1\right)=p p(x1)=p
p ( x 2 ) = 1 − p p\left(x_2\right)=1-p p(x2)=1−p
q ( x 1 ) = q q\left(x_1\right)=q q(x1)=q
q ( x 2 ) = 1 − q q\left(x_2\right)=1-q q(x2)=1−q
真实分布的信息熵为0
此时KL散度等于交叉熵
如果没有真实分布则KL散度
CrossEntropyLoss()
entropy = nn.CrossEntropyLoss()
input = torch.tensor([[-0.7715,-0.6205,-0.2562]])
target = torch.tensor([0])
output = entropy(input, target)
l o s s ( x , c l a s s ) = − l o g e x p ( x [ c l a s s ] ) ∑ j e x p ( x [ j ] ) = − x [ c l a s s ] + l o g ∑ j e x p ( x [ j ] ) loss\left(x,class\right)=-log\frac{exp\left(x\left[class\right]\right)}{\sum_{j}exp\left(x\left[j\right]\right)}=-x\left[class\right]+log\sum_{j}exp\left(x\left[j\right]\right) loss(x,class)=−log∑jexp(x[j])exp(x[class])=−x[class]+log∑jexp(x[j])
注意以e为底数
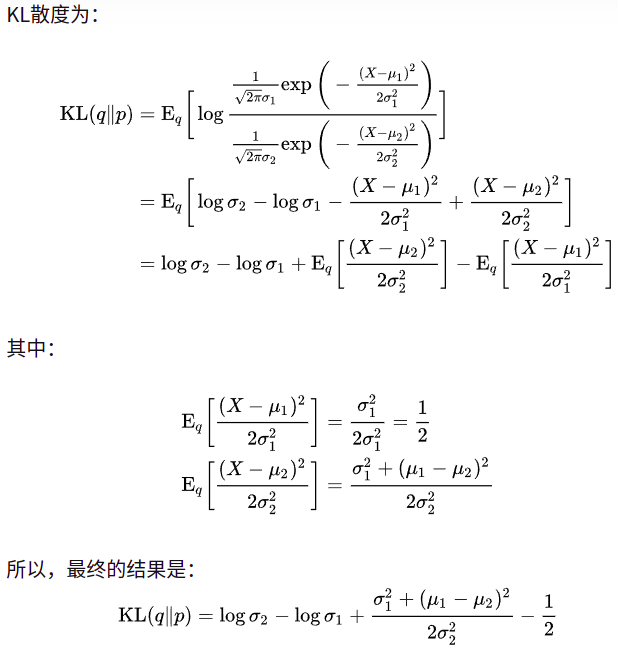
四、正态分布KL散度
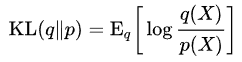

版权声明
本文为[qq1033930618]所创,转载请带上原文链接,感谢
https://blog.csdn.net/qq_51326691/article/details/123898734
边栏推荐
猜你喜欢
随机推荐
《Attention in Natural Language Processing》翻译
自定义钉钉机器人进行报警
项目文件“ ”已被重命名或已不在解决方案中、未能找到与解决方案关联的源代码管理提供程序——两个工程问题
可视化常见绘图(五)散点图
presto日期函数的使用
Intelligent communication solution of Hainan Phoenix Airport
通过sparksql读取presto中的数据存到clickhouse
pytorch:关于GradReverseLayer实现的一个坑
Take you to travel in space, and American photography technology provides comprehensive technical support for aerospace creative applet
Urban emergency management - urban emergency communication command and dispatching system
Wireless communication system for large-scale sports events
美摄助力百度“度咔剪辑”,让知识创作更容易
可视化常见问题解决方案(七)画图刻度设置解决方案
南方投资大厦SDC智能通信巡更管理系统
可视化常见绘图(四)柱状图
jvm知识点汇总-持续更新
PyTorch 17. GPU concurrency
(一)OpenPAI jupyter jupyterhub jupyterlab 方案比较
基于51单片机的三路超声波测距系统(定时器方式测距)
北峰通信助力湛江市消防支队构建PDT无线通信系统