当前位置:网站首页>[hdu6868] absolute math (pusher + Mobius inversion)
[hdu6868] absolute math (pusher + Mobius inversion)
2022-04-23 09:43:00 【Zimba_】
The question :
Make f ( n ) = ∑ d ∣ n ∣ μ ( d ) ∣ f(n)=\sum_{d|n}|\mu (d)| f(n)=∑d∣n∣μ(d)∣. T T T Group inquiry , Each group is given one n n n and m m m, seek ∑ i = 1 m f ( n i ) \sum_{i=1}^{m}f(ni) ∑i=1mf(ni).
( 1 ≤ T ≤ 1 0 4 , 1 ≤ n , m ≤ 1 0 7 ) (1\leq T\leq 10^{4},1\leq n,m\leq 10^{7}) (1≤T≤104,1≤n,m≤107)
deduction :
First, according to the Mobius function μ ( n ) \mu (n) μ(n) The definition of can be known , When n n n When there is a square factor , ∣ μ ( n ) ∣ = 0 |\mu (n)|=0 ∣μ(n)∣=0, otherwise ∣ μ ( n ) ∣ = 1 |\mu (n)|=1 ∣μ(n)∣=1.
therefore f ( n ) f(n) f(n) It means n n n Of the factors , Number of factors without square factor .
We will n n n Find out all the qualitative factors , Because there can't be a square factor , So the number of times of each prime factor is either 0 0 0, Either for 1 1 1. Got it. f ( n ) = 2 w ( n ) f(n)=2^{w(n)} f(n)=2w(n), among w ( n ) w(n) w(n) Express n n n How many different qualitative factors .
According to the above formula , You can find f ( a b ) = f ( a ) f ( b ) f ( g c d ( a , b ) ) = 2 w ( a ) + w ( b ) − w ( g c d ( a , b ) ) f(ab)=\frac{f(a)f(b)}{f(gcd(a,b))}=2^{w(a)+w(b)-w(gcd(a,b))} f(ab)=f(gcd(a,b))f(a)f(b)=2w(a)+w(b)−w(gcd(a,b)).
It's out g c d gcd gcd after , We consider Mobius inversion , We need to put g c d gcd gcd Bring up , The original formula becomes .
∑ i = 1 m f ( n i ) = ∑ g = 1 m i n ( n , m ) 2 − w ( g ) ∑ i = 1 m 2 w ( n ) + w ( i ) [ g = g c d ( n , i ) ] \sum_{i=1}^{m}f(ni)=\sum_{g=1}^{min(n,m)}2^{-w(g)}\sum_{i=1}^{m}2^{w(n)+w(i)}[g=gcd(n,i)] i=1∑mf(ni)=g=1∑min(n,m)2−w(g)i=1∑m2w(n)+w(i)[g=gcd(n,i)]
Now start Mobius inversion , Make y ( g ) = ∑ i = 1 m 2 w ( n ) + w ( i ) [ g = g c d ( n , i ) ] y(g)=\sum_{i=1}^{m}2^{w(n)+w(i)}[g=gcd(n,i)] y(g)=∑i=1m2w(n)+w(i)[g=gcd(n,i)].
Then make Y ( d ) = ∑ d ∣ g y ( g ) Y(d)=\sum_{d|g}y(g) Y(d)=∑d∣gy(g), namely ,
Y ( d ) = ∑ d ∣ g ∑ i = 1 m 2 w ( n ) + w ( i ) [ g = g c d ( n , i ) ] = ∑ i = 1 m ∑ d ∣ n ∑ d ∣ i 2 w ( n ) + w ( i ) Y(d)=\sum_{d|g}\sum_{i=1}^{m}2^{w(n)+w(i)}[g=gcd(n,i)]=\sum_{i=1}^{m}\sum_{d|n}\sum_{d|i}2^{w(n)+w(i)} Y(d)=d∣g∑i=1∑m2w(n)+w(i)[g=gcd(n,i)]=i=1∑md∣n∑d∣i∑2w(n)+w(i)
Then there are y ( g ) = ∑ g ∣ d μ ( d / g ) Y ( d ) y(g)=\sum_{g|d}\mu (d/g)Y(d) y(g)=∑g∣dμ(d/g)Y(d).
The original formula becomes ,
∑ g = 1 m i n ( n , m ) y ( g ) = ∑ g = 1 m i n ( n , m ) 2 − w ( g ) ∑ g ∣ d μ ( d / g ) ∑ d ∣ n ∑ i = 1 m ∑ d ∣ i 2 w ( n ) + w ( i ) = 2 w ( n ) ∑ i = 1 m 2 w ( i ) ∑ d ∣ n ∑ d ∣ i ∑ g ∣ d 2 − w ( g ) μ ( d / g ) \sum_{g=1}^{min(n,m)}y(g)=\sum_{g=1}^{min(n,m)}2^{-w(g)}\sum_{g|d}\mu(d/g)\sum_{d|n}\sum_{i=1}^{m}\sum_{d|i}2^{w(n)+w(i)}=2^{w(n)}\sum_{i=1}^{m}2^{w(i)}\sum_{d|n}\sum_{d|i}\sum_{g|d}2^{-w(g)}\mu(d/g) g=1∑min(n,m)y(g)=g=1∑min(n,m)2−w(g)g∣d∑μ(d/g)d∣n∑i=1∑md∣i∑2w(n)+w(i)=2w(n)i=1∑m2w(i)d∣n∑d∣i∑g∣d∑2−w(g)μ(d/g)
We make G ( d ) = ∑ g ∣ d 2 − w ( g ) μ ( d / g ) G(d)=\sum_{g|d}2^{-w(g)}\mu(d/g) G(d)=∑g∣d2−w(g)μ(d/g), Sure o ( n l o g n ) o(nlogn) o(nlogn) Preprocess this function , Then turn the formula .
A N S = 2 w ( n ) ∑ i = 1 m 2 w ( i ) ∑ d ∣ n ∑ d ∣ i G ( d ) = 2 w ( n ) ∑ d ∣ n G ( d ) ∑ i = 1 m ∑ d ∣ i 2 w ( i ) = 2 w ( n ) ∑ d ∣ n G ( d ) ∑ i = 1 ⌊ m d ⌋ 2 w ( i d ) ANS=2^{w(n)}\sum_{i=1}^{m}2^{w(i)}\sum_{d|n}\sum_{d|i}G(d)=2^{w(n)}\sum_{d|n}G(d)\sum_{i=1}^{m}\sum_{d|i}2^{w(i)}=2^{w(n)}\sum_{d|n}G(d)\sum_{i=1}^{\lfloor \frac{m}{d} \rfloor}2^{w(id)} ANS=2w(n)i=1∑m2w(i)d∣n∑d∣i∑G(d)=2w(n)d∣n∑G(d)i=1∑md∣i∑2w(i)=2w(n)d∣n∑G(d)i=1∑⌊dm⌋2w(id)
Code :
Insert a code chip here
版权声明
本文为[Zimba_]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204230621425148.html
边栏推荐
- 108. Convert an ordered array into a binary search tree
- Learn FPGA (from Verilog to HLS)
- STM32 and FreeRTOS stack parsing
- 三、6【Verilog HDL】基础知识之门级建模
- JS DOM event
- 1 + X cloud computing intermediate -- script construction, read-write separation
- Kettle experiment
- Comparison of overloading, rewriting and hiding
- Unfortunately, I broke the leader's confidential documents and spit blood to share the code skills of backup files
- Dropout技术之随机神经元与随机深度
猜你喜欢
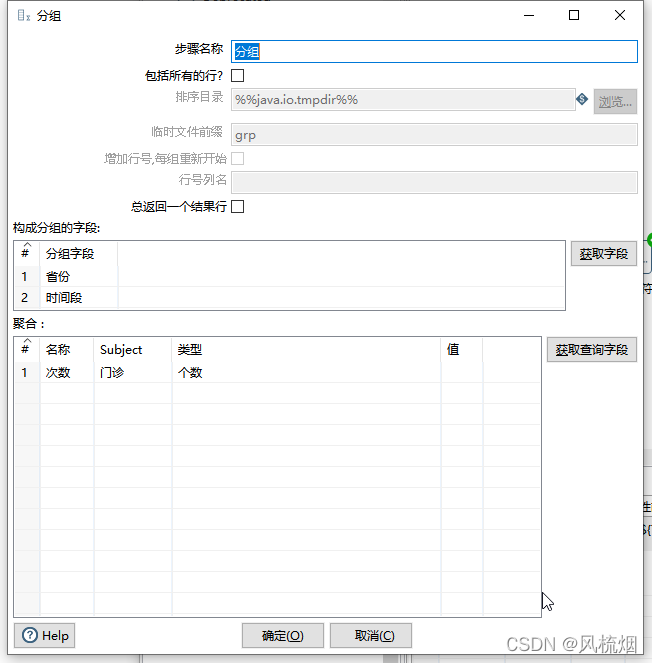
Kettle experiment

653. Sum of two IV - input BST

【读书笔记】《Verilog数字系统设计教程》 第5章 条件语句、循环语句和块语句(附思考题答案)

PHP笔记(一):开发环境配置

重载、重写、隐藏的对比

阿里云架构师解读四大主流游戏架构

Go language learning notes - exception handling | go language from scratch
![[educational codeforces round 80] problem solving Report](/img/54/2fd298ddce3cd3e28a8fe42b3b8a42.png)
[educational codeforces round 80] problem solving Report

成功的DevOps Leader 应该清楚的3个挑战

NLLLoss+log_ SoftMax=CE_ Loss
随机推荐
PHP notes (I): development environment configuration
Go language learning notes - slice, map | go language from scratch
Give the method of instantiating the object to the new object
kernel-pwn学习(3)--ret2user&&kernel ROP&&QWB2018-core
Random neurons and random depth of dropout Technology
Golang force buckle leetcode 396 Rotation function
Alibaba cloud architects interpret the four mainstream game architectures
Kernel PWN learning (4) -- double fetch & 0ctf2018 baby
kernel-pwn学习(4)--Double Fetch&&0CTF2018-baby
《数字电子技术基础》3.1 门电路概述、3.2 半导体二极管门电路
STM32 and FreeRTOS stack parsing
JS DOM learn three ways to create elements
JS what is an event? Event three elements and operation elements
Example of data object mask used by SAP translate
SAP debug debug for in, reduce and other complex statements
RSA 加密解密签名验签
[reading notes] Chapter 5 conditional statements, circular statements and block statements of Verilog digital system design tutorial (with answers to thinking questions)
ABAP implementation publishes restful services for external invocation example
MacOS下使用CLion编译调试MySQL8.x
ES-aggregation聚合分析